В настоящее время существует большое количество способов записи и обработки получаемой в когерентном свете оптической информации о структуре того или иного физического объекта. Cамый распространенный из них состоит в получении с помощью оптической системы изображения интересующего объекта, его регистрации с использованием возможностей фото- и видеотехники и в последующей апостериорной обработке изображения. Другой способ, также получивший широкое распространение, основан на получении голограммы объекта. Этот способ, в отличие от первого, позволяет регистрировать информацию не только о распределении интенсивности света, отраженного или излучаемого объектом, но и о распределении фазы световых колебаний. Последнее обстоятельство создает дополнительные возможности по корректировке характеристик изображения. Однако свойства когерентных оптических систем , даже состоящих из традиционных оптических элементов (линзы, зеркала, киноформы, диафрагмы, маски и т.д.), не сводятся только к способности формировать оптические изображения. В ряде случаев их можно рассматривать как некие оптические процессоры, осуществляющие определенные математические преобразования, например, фурье-преобразования, по отношению к двумерной функции, определяющей распределение комплексной амплитуды на входе системы. Несмотря на кажущееся различие указанных вариантов использования оптических систем, их теоретическое описание имеет много общего.

В связи с этим изложение материала данной главы начнем с построения общей теории оптических систем.

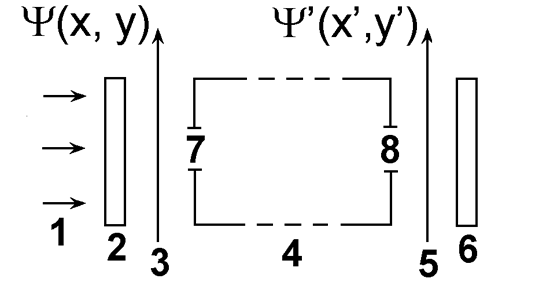
В самом общем виде функциональная схема записи и обработки оптической информации приведена на рис. 3.1.1. Плоская монохроматическая волна 1 освещает объект 2, который размещают во входной (предметной) плоскости системы 3. Излучение, прошедшее объект или отраженное от него, попадает во входное отверстие (входной зрачок) 7 оптической системы 4. Пройдя элементы оптической системы, излучение выходит из выходного отверстия (выходного зрачка) 8 и формирует в выходной плоскости (плоскости изображений) 5 изображение объекта. Вблизи плоскости изображений располагается светочувствительный элемент 6 регистрирующей системы (фотопластина, матрица фотоприемников и т.д.)

В тех случаях, когда оптическая система играет роль оптического процессора, у входной плоскости системы вместо объекта 2 располагается преобразователь входных сигналов. Он, пространственно модулируя падающую на него световую волну, преобразует информацию, поступающую от некоторого источника во входной оптический сигнал. В одном случае преобразователь может представлять собой слайд, на котором информация записана в виде изменяющего коэффициента пропускания. В другом случае в качестве преобразователя может использоваться слой жидкости, рельеф поверхности которой изменяется под действием ультразвуковых волн или электронного пучка.

Рис. 3.1.1. Схема оптической обработки информации. 1-плоская монохроматическая волна; 2-объект; 3-входная (предметная) плоскость; 4-оптическая система; 5-выходная плоскость (плоскость изображения); 6-светочувствительный элемент; 7-входное отверстие (входной зрачок); 8-выходное отверстие (выходной зрачок).

, (3.1.1)

где  - некий линейный оператор. Линейность преобразования означает, что выходной сигнал от суммы входных сигналов равен сумме выходных сигналов от каждого входного сигнала в отдельности.

Используя свойство d -функции Дирака, можно представить функцию  в виде

(3.1.2)

Подставляя (3.1.2) в (3.1.1) и учитывая линейность оператора , можно записать

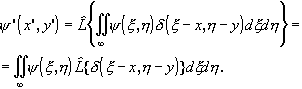(3.1.3)

Таким образом, выходной сигнал  может быть представлен в виде суммы (интеграла) элементарных откликов  с весовыми коэффициентами . Поскольку d - функция  моделирует узкий и высокий "импульс" в точке  (точечный источник света), функцию

(3.1.4)

называют импульсным откликом системы. Учитывая последнее обозначение, выражению (3.1.3) придаем вид

. (3.1.5)

Импульсный отклик  называют также переходной функцией данной оптической системы, а выражение (3.1.5) получило название "интеграл суперпозиции".

Качество оптических систем во многом определяется тем, в какой степени им присуще свойство изопланарности. Под изопланарностью понимают инвариантность к пространственным смещениям, обеспечивающую выполнение соотношения

(3.1.6)

Форма выходного сигнала в изопланарной системе, тем самым, не зависит от пространственных смещений входного сигнала. Хотя реальные оптические системы редко бывают изопланарными по всей плоскости входного сигнала (изопланарность имеет место лишь на отдельных участках), все рассматриваемые системы мы в дальнейшем будем считать изопланарными. Это допущение позволяет нам представить переходную функцию системы  в более простом виде, считая ее зависящей от разности значений соответствующих координат

(3.1.7)

Интеграл суперпозиции (3.1.5) при этом принимает вид интеграла свертки

(3.1.8)

Применим к левой и правой части соотношения (3.1.8) преобразование Фурье

(3.1.9)

Из теоремы свертки следует, что

(3.1.10)

поэтому выражение (3.1.9) может быть представлено в виде

(3.1.11)

Введем следующие обозначения:

(3.1.12)

Функцию  принято называть передаточной функцией системы.

Перепишем выражение (3.1.11) с учетом обозначений (3.1.12)

(3.1.13)

Из последнего соотношения видно, что спектр пространственных частот выходного сигнала равен произведению спектра частот входного сигнала и передаточной функции. Выражение (3.1.13), как мы убедимся ниже, играет фундаментальную роль в теории систем записи и обработки оптической информации. Теоретический анализ мы начнем с простейшей оптической системы, состоящей всего лишь из одной линзы.

Как уже ранее отмечалось, линза является элементом, осуществляющим квадратичную фазовую модуляцию. Это означает, что распределение поля падающей на линзу волны Y x (x ,h ) будет связано с распределением поля световых колебаний за линзой Y 'x (x ,h ) соотношением

(3.2.1),

где так называемая модуляционная характеристика линзы Т(x , h ) равна
 

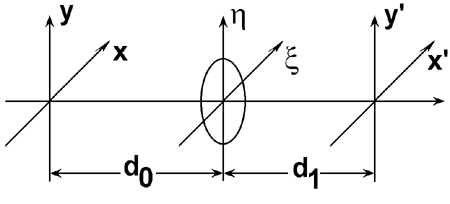Рис. 3.2.1. Однолинзовая система.

(3.2.2)

где

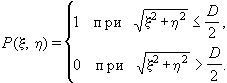(3.2.3)

Рассчитаем теперь переходную функцию однолинзовой системы. Для простоты будем считать, что апертура линзы существенно превосходит апертуру падающего на него светового пучка. Возьмем за основу формулу (1.2.40) гл. 1, исключив из нее легко учитываемый постоянный фазовый множитель -iexp(ikz). В соответствии с этой формулой входной сигнал y (х,у) после прохождения расстояния d₀ преобразуется в сигнал

(3.2.4).

Согласно (3.2.1 - 3.2.3), сразу за линзой сигнал принимает вид

(3.2.5).

Еще раз воспользовавшись формулой (1.2.40), получаем выражение для сигнала в выходной плоскости (после прохождения на расстоянии d1)

(3.2.6).

Используя выражения (3.2.4-3.2.6), запишем теперь в явном виде связь между входным y (х,у) и выходным y (х',у') сигналами

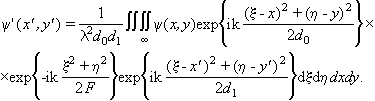(3.2.7).

Отсюда видно, что переходная функция однолинзовой системы равна

 (3.2.8)

Положим d0=d1=F. В этом случае (3.2.8) принимает вид

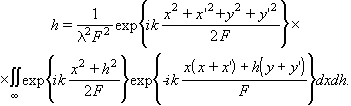(3.2.9)

Используя далее соотношение

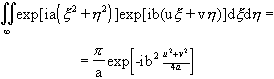(3.2.10)

и, полагая , получаем для переходной функции простое выражение

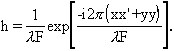(3.2.11)

Если теперь ввести обозначения

(3.2.12)

то интеграл суперпозиции (3.2.7) можно привести к виду

(3.2.13)

Отсюда видно, что при выполнении условия d0=d1=F линза выполняет Фурье-преобразование сигнала: ее задняя фокальная плоскость является спектральной плоскостью входного сигнала. Таким образом, линза может предельно просто выполнять математическую операцию, представляющую трудность даже для сложных электронных устройств.

Заметим, что спектр с точностью до легко учитываемого фазового множителя будет формироваться в фокальной плоскости даже в том случае, когда d0>F. При этом условии выражение (3.2.7) приводится к виду (промежуточные выкладки мы опускаем)

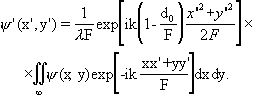(3.2.14)

Фазовый множитель

, (3.2.15)

не зависящий от вида входного сигнала, легко учитывается при последующей обработке.

Предположим, что плоский предмет, находящийся на расстоянии d0 перед положительной линзой, освещен монохроматическим светом. Обозначим комплексное поле непосредственно за предметом через y (x,y) Распределение поля, которое возникает на расстоянии d1 за линзой, обозначим через y '(x',y'). Наша задача - определить условия, при которых распределение поля y ' можно с уверенностью назвать "изображением" распределения поля в плоскости предмета y .

Ввиду линейности явления распространения волн поле y ' можно представить в виде интеграла суперпозиции (3.1.5). Тем самым свойства системы, создающей изображение, будут полностью описаны с помощью импульсного отклика h (см. (3.2.8)).

Чтобы оптическая система давала высококачественное изображение, поле y ' должно как можно меньше отличаться от y . Это означает, что импульсный отклик должен приближенно походить на d -функцию, т.е.

  (3.2.16)

где K - комплексная постоянная, М - увеличение системы, а знак плюс или минус учитывает возможность как прямого, так и обратного изображения. Поэтому "плоскостью изображения" мы будем называть ту плоскость, где (3.2.16) выполняется лучше всего.

Преобразуем (3.2.8) к виду

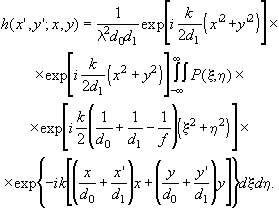(3.2.17)

Соотношения (3.2.17) играет важную роль при определении зависимости между y и y '. Однако без дальнейших упрощений трудно определить условия, при которых распределение y ' можно с уверенностью назвать изображением распределения y .

Самые неприятные члены в приведенном выше выражении для импульсного отклика - это члены, содержащие квадратичные фазовые множители. Заметим, что два из них:

(3.2.18)

не зависят от координат линзы (x , h ). Эти члены определяют фазовое искривление в плоскостях (x',y') и (x,y). Если бы мы решили рассматривать формирование изображения между двумя сферическими поверхностями, а не между двумя плоскостями, эти члены можно было бы исключить. Однако можно показать, что и в случае формирования изображения между двумя плоскостями оба эти члена несущественны.

Опуская множитель , заметим, что в подавляющем большинстве представляющих интерес случаев конечной целью задачи формирования изображения является получение некоторого распределения света, которое будет воспринято детектором, реагирующим только на интенсивность (например, фотопленкой). Так как рассматриваемый член изменяет только распределение фазы, он никак не будет влиять на результаты измерения интенсивности и, следовательно, может быть опущен.

К сожалению, от фазового множителя  не удается освободиться столь же просто, поскольку он зависит от переменных интегрирования (x,y) интеграла суперпозиции. Однако в большинстве случаев, представляющих интерес, от него тоже можно избавиться. Если система, создающая изображение, ведет себя приблизительно так же, как идеальная система, для которой справедливо соотношение (3.2.16), то амплитуда волны в точке с координатами (x',y') будет определяться вкладом только очень малой области в пространстве предмета с центром в точке, соответствующей идеальному геометрическому изображению (рис. 3.2.2).
 

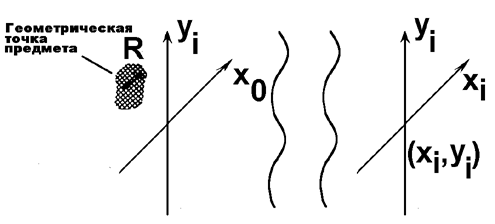Рис. 3.2.2. Область R, в которой функция h для точки с координатами (x',y') имеет значительную величину.

Если внутри этой малой области аргумент  изменяется не более чем на долю радиана, то можно использовать приближение

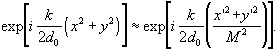(3.2.19)

Теперь экспоненциальный член можно опустить, так как он не зависит от (x, y) и следовательно, не влияет на результат измерения интенсивности в плоскости (x',y').

Воспользовавшись приведенными соображениями, перепишем выражение для импульсного отклика в виде

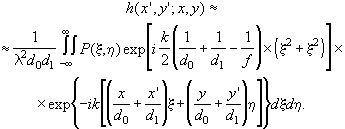(3.2.20)

Чтобы получить совсем простой результат, рассмотрим случай, когда плоскость наблюдения расположена на таком расстоянии d1 от линзы, что удовлетворяется соотношением

. (3.2.21)

Это соотношение известно из геометрической оптики, где оно называется формулой линзы. Соотношение (3.2.21) определяет расположенную за линзой точку, в которой пересекаются лучи, исходящие из одной точки предмета (точка изображения). В приближении геометрической оптики выполнение формулы линзы означает, что импульсный отклик системы достаточно близок к идеальному. Предположение о выполнении формулы линзы позволяет свести импульсный отклик к виду

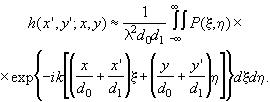(3.2.22)

Определяя увеличение системы как

(3.2.23)

находим последний упрощенный вид импульсного отклика

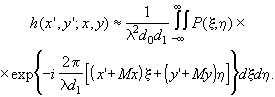(3.2.24)

Таким образом, если формула линзы справедлива, то импульсный отклик соответствует картине дифракции Фраунгофера на апертуре линзы, причем центр картины находится в точке изображения .

Перейдем теперь к анализу соотношения между предметом и изображением. Рассмотрим сначала свойства изображения, предсказываемые геометрической оптикой. Чтобы найти это идеальное изображение, допустим, что длина волны стремится к нулю. В этом случае дифракционные эффекты становятся несущественными. Производя замену переменных

(3.2.25)

выражение для импульсного отклика (3.2.24) можно переписать в виде

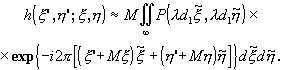(3.2.26)

Так как  стремится к нулю, область значений (), где функция зрачка Р равна единице, будет безгранично увеличиваться, что дает возможность заменить Р единицей, оставив те же пределы интегрирования. Таким образом,

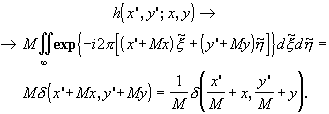(3.2.27)

Представляя этот результат в интеграл суперпозиции (3.2.16), получаем соотношение, связывающее распределения амплитуды в точках предмета и в точках изображения

(3.2.28)

Отсюда следует, что изображение, получаемое в приближении геометрической оптики, представляет собой точную копию изображения.

Выводы геометрической оптики, конечно, приближенны. Более точное представление о соотношении между предметом и изображением можно получить только при учете дифракционных эффектов. Чтобы найти такое соотношение, вернемся к выражению (3.2.26) для импульсного отклика и произведем следующую дополнительную замену переменных:

(3.2.29)

Импульсный отклик в этом случае будет равен

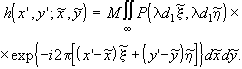(3.2.30)

Заметим, что h теперь пространственно-инвариантная величина, зависящая только от разности координат . С введением еще одного определения

(3.2.31)

распределение поля в плоскости изображения принимает вид

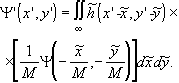(3.2.32)

В этом выражении мы узнаем свертку импульсного отклика  и идеального изображения. Для удобства определим новую функцию

(3.2.33)

Свертку (3.2.32) тогда можно переписать в упрощенном виде:

 (3.2.34)

где

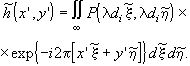(3.2.35)

Соотношения (3.2.34) и (3.2.35) представляют собой конечный результат настоящего анализа. Они показывают, что при учете дифракционных эффектов изображение нельзя больше считать точной копией предмета. Полученное изображение дает несколько сглаженный облик предмета, что является следствием неравенства нулю ширины импульсного отклика . Это сглаживание может привести к значительному ослаблению мелких деталей предмета и соответственно к потере точности воспроизведения изображения. Точно такое же явление можно наблюдать в случае, когда электрический сигнал проходит через линейную электрическую схему. Если длительность импульсного отклика схемы велика по сравнению с "временем пульсаций" входного сигнала, то схема будет сглаживать входной сигнал. Таким образом, быстрые изменения входного сигнала не будут воспроизводиться на выходе.

При рассмотрении свойств системы линз будем считать, что все элементы, создающие изображение, помещены в один "черный" ящик" и что основные свойства системы можно полностью описать, определяя только конечные свойства этого устройства.

Согласно рис. 3.1.1, входом этого черного ящика служит входной зрачок, представляющий собой отверстие конечных размеров (эффективнное или действительное), через которое должен проходить свет прежде, чем он достигнет элементов, создающих изображение, а выходом - выходной зрачок (также эффективный или действительный), представляющий собой отверстие конечных размеров, через которое свет проходит после создающих изображение элементов на пути к плоскости изображения. Обычно считают, что путь света между входной и выходной плоскостями может быть достаточно полно описан в приближениях геометрической оптики. Таким образам, конечный размер обоих зрачков можно найти, строя по законам геометрической оптики проекцию наименьшей апертуры системы соответственно в пространстве предметов и пространстве изображений. Поскольку размеры получающихся зрачков определяются размерами изображенния эффективного отверстия, существующего где-то внутри системы, они могут быть меньше действительных физических размеров отверстий в входной и выходной плоскостях. Заметим, что при таком определении входной зрачок всегда является изображением выходнного зрачка и наоборот.

Оптическая система называется дифракционно ограниченной, если она преобразует расходящуюся сферическую волну, исходящую из любого точечного источника, в новую идеальную сферическую волну, которая сходится в точке, лежащей в плоскости изображения. Таким образом, конечное свойство дифракционно ограниченной системы линз заключается в том, что она преобразует расходящуюся сферическую волну, падающую на входной зрачок, в сходящуюся сферическую волну, выходящую через выходной зрачок. Для любой реальной оптической системы это свойство выполняется в лучшем случае только для конечной области в плоскости предмета. Если рассматриваемый предмет не выходит за пределы этой области, систему можно отнести к дифракционно ограниченной. Если в действительности фронт волны от точечного источника после выходного зрачка значительно отличается от идеальной сферической формы, то говорят, что оптическая система имеет аберрации.

Геометрическая оптика с достаточной точностью описывает прохождение света от входного зрачка к выходному, поэтому дифракционные эффекты играют заметную роль только на пути света от предмета к входному зрачку и от выходного зрачка к изображению. Действительно, все ограничения, налагаемые дифракцией, можно связать с любым из этих двух участков пути распространения света. Утверждения о том, что разрешение изображения ограничивается входным зрачком конечных размеров или выходным зрачком конечных размеров, полностью эквивалентны. Основная причина эквивалентности заключается в том, что один зрачок представляет собой просто изображение другого.

Представление о том, что обсуждаемые дифракционные эффекты обусловлены входным зрачком конечных размеров, было впервые введено Эрнстом Аббе в 1873г. Согласно теории Аббе, только определенная часть дифракционных максимумов, созданных сложным предметом, пропускается входным зрачком конечных размеров. Не пропускаются зрачком те максимумы, которые соответствуют высокочастотным составляющим предмета. Это положение иллюстрирует рис. 3.3.1, где предметом служит простая решетка, а оптическая система состоит из одной положительной линзы.
 

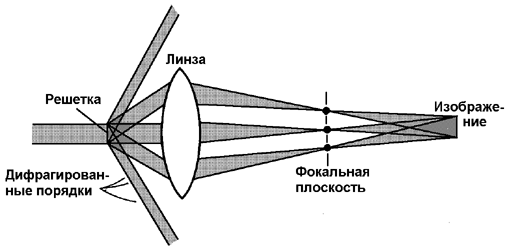Рис. 3.3.1. Формирование изображения по Аббе.

В 1896 г. Релей высказал другую, фактически эквивалентную точку зрения, в соответствии с которой дифракционные эффекты обусловлены выходным зрачком конечных размеров. Тем самым, на сложные оптические системы могут быть перенесены соотношения (3.2.34) и (3.2.35), полученные для однолинзовой системы, путем замены апертурной функции линзы Р на апертурную функцию выходного зрачка системы. К сложным системам, формирующим изображение непосредственно применимо понятие передаточной функции.

Передаточная функция Н определяется как фурье-образ переходной функции , которая в свою очередь определяется преобразованием Фурье от фукции выходного зрачка (переходная функция будет выражаться формулой (3.2.35) в предположении,что функция P относится к выходному зрачку)

Таким образом, мы приходим к выводу, что для дифракционно ограниченной системы

(3.3.1)

Это крайне важное соотношение, так как оно дает информацию относительно поведения дифракционно ограниченных когерентных систем в частотной области. Так как функция зрачка Р всегда равна или единице или нулю, то же самое справедливо и для передаточной функции. Это, естественно, означает, что в частотной области дифракционно ограниченная система имеет конечную полосу пропускания, внутри которой все частотные составляющие пропускаются без искажения амплитуды и фазы. На границе этой полосы пропускания частотный отклик сразу падает до нуля, в силу чего частотные составляющие вне полосы пропускания полностью подавляются.

Поскольку функция зрачка системы играет принципиальную роль в формировании структуры изображения, возникает вопрос о возможности подбора такого амплитудного пропускания зрачка системы, при котором ослабляются боковые лепестки дифракционной картины резко очерченной диафрагмы. Появление боковых лепестков в дифракционной картине аналогично эффекту оптических выбросов или эффекту Гиббса. Как известно, эффект Гиббса полностью исчезает, если от зрачка, амплитудное пропускание которого описывается прямоугольным импульсом, перейти к зрачку, описываемому треугольным импульсом. Наиболее подходящей формой зрачка является такая, амплитудное пропускание которой описывается функцией Гаусса. Действительно, в этом случае картина дифракции далекого поля описывается фурье- образом зрачка, а фурье-образ функции Гаусса равен функции Гаусса. Боковые лепестки при этом полностью исчезают. Процесс аподизации сопровождается неизбежным уширением основного пика дифракционной картины.

Mетод аподизации, основанный на сглаживании функции пропускания зрачка системы, является весьма эффективным способом улучшения пространственной структуры оптического сигнала. На рис. 3.3.2 приведены результаты аподизации картины дифракции далекого поля. С помощью аподизации удается разделить изображение двух близко расположенных предметов, когда они очень сильно отличаются между собой по интенсивности.

3.3.2. Роль аподизации
 

Рис. 3.3.2. Влияние аподизации на вид картины дифракции далекого поля. Вверху - дифракция без аподизации; внизу - после аподизации.

 

Если оптическая система является дифракционно ограниченной, то импульсный отклик (при когерентном освещении), как мы видели, представляет собой картину дифракции Фраунгофера на выходном отверстии с центром в точке идеального изображения. Это обстоятельство подсказывает удобный прием, который позволит непосредственно учесть аберрации в наших предыдущих результатах. В частности, в случае искажения волнового фронта можно представить, что выходной зрачок освещается идеальной сферической волной, но в пределах отверстия находится фазовая пластинка, деформирующая выходящий из зрачка фронт волны. Если фазовая ошибка в точке  выходного зрачка изображается как , где , а W- эффективная погрешность длины пути, то комплексный коэффициент пропускания Р воображаемой фазовой пластинки можно представить в виде

(3.4.1)

Комплексную функцию Р можно считать обобщенной функцией зрачка. Импульсный отклик когерентной системы с аберрациями представляет собой просто картину дифракции Фраунгофера на отверстии с коэффициентом пропускания Р.

Передаточная функция при наличии аберрации запишется следующим образом:

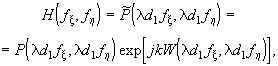(3.4.2)

где fx и fh - пространственные частоты в направлениях x и h .

Очевидно, что в случае когерентного освещения ограничение полосы пропускания передаточной функции, которое обусловлено конечным размером выходного зрачка, не зависит от наличия аберраций. Аберрации вводят только фазовые искажения в пределах полосы пропускания. Разумеется, фазовые искажения могут оказывать определенное влияние на точность воспроизведения.

В теории оптических систем эффективную погрешность длины пути W принято оценивать по расстояниям отделяющих волновой фронт точечного источника вблизи выходного зрачка реальной системы (c аберрациями) от сферического волнового фронта, формируемого идеальной системой (без аберраций). Тем самым, при оценке аберраций сферический волновой фронт идеальной системы выступает в качестве сферы сравнения. Если ввести в плоскости выходного зрачка полярную систему координат с радиальной координатой  (R - внешняя апертура выходного зрачка) и азимутальной координатой j , то W можно представить в виде:

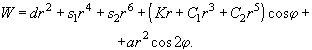(3.4.3)

Коэффициенты в этом выражении имеют следующий смысл:

d представляет дефокусировку или кривизну поля, т.е. максимальное отклонение на краю зрачка (r=1) сферы сравнения от волновой поверхности (которая является сферической, если эта аберрация единственная);

s1 - коэффициент сферической аберрации 3-го порядка. Это максимальное отклонение на краю зрачка деформированной волновой поверхности от сферы сравнения, имеющей центр в параксиальном фокусе (острие геометрической каустики);

s2 - коэффициент сферической аберрации 5-го порядка при тех же условиях;

K - параметр, соответствующий возможному покачиванию сферы сравнения;

C1 - коэффициент комы 3-го порядка, т.е. максимальное отклонение на краю отверстия от сферы сравнения, центр которой совпадает с параксиальным фокусом волновой поверхности, соответствующей коме (если эта аберрация единственная);

C2 - коэффициент комы 5-го порядка при тех же условиях;

a - коэффициент астигматизма, т.е. максимальное отклонение астигматической волновой поверхности от сферы сравнения.

(3.5.1)

(3.5.2)

o, r и j o, j r - соответственно амплитуды и фазы колебаний. Если в плоскости наблюдения расположить фотопластинку с идеальной линейной по интенсивности фотоэмульсией, то она зарегистрирует следующее распределение интенсивности:

(3.5.3)

После соответствующей обработки пропускание пластинки станет пропорционально I.

Если теперь эту пластинку осветить опорной волной R, то поле на выходе пластинки будет иметь вид

(3.5.4)

Последнее выражение составляет теоретическую основу голографии. В нем первое слагаемое  представляет собой поле опорной волны R, амплитуда которой промодулирована коэффициентом ; второе слагаемое  - поле объектной волны, амплитуда которой промодулирована коэффициентом r². Если в качестве опорной волны используется плоская волна, то  и модуляция исчезает; объектная волна при этом равномерно ослабевает в соответствии с коэффициентом rо2. Наконец, третье слагаемое в выражении (3.5.4)  - описывает волну, комплексно-сопряженную с объектной волной. Оно несет информацию, хотя и очень близкую к информации об объекте, но отличающуюся от объектной волны наличием обратной фазы.

Остановимся теперь на конкретных схемах голографической записи и восстановления изображений. Наибольшее распространение получила схема, предложенная в 1962 г. американскими учеными Лейтом и Упатниексом. Ее упрощенный вариант приведен на рис. 3.5.1.
 

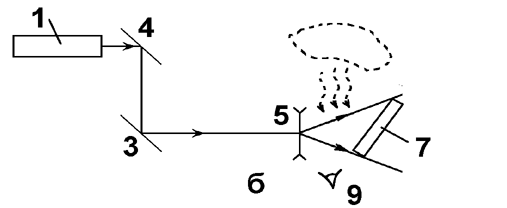Рис. 3.5.1. Схема записи (а) и восстановления (б) изображения: 1 - лазер; 2 - светоделительная пластина; 3,4 - поворотные зеркала; 5,6 - линзы; 7 - голографическая пластина; 8 - объект; 9 - наблюдатель; О - объектная волна; R - опорная волна.

Как видно из рисунка, при восстановлении изображения используется пучок, который при записи выполняет роль опорного. Положение восстановленного изображения полностью соответствует положению объекта.

Другая схема, ориентированная на получение так называемых голограмм Фурье, будет далее рассмотрена более подробно.

На схеме плоскость, в которой размещается пленка с изображениями объектов, обозначена буквой П, а плоскость, в которой формируется голограмма, - буквой Г. Плоскости П и Г совпадают с фокальными плоскостями линзы Л3. На плоскость П падает плоская волна когерентного света, создаваемая источником S. От этого же источника в плоскости П с помощью линз Л1 и Л2 формируется точечный источник S0, создающий опорную волну. Опорный и предметный пучки собираются линзой Л3 и в плоскости Г создают интерференционную картину, которая регистрируется помещенной в этой плоскости фотопленкой.

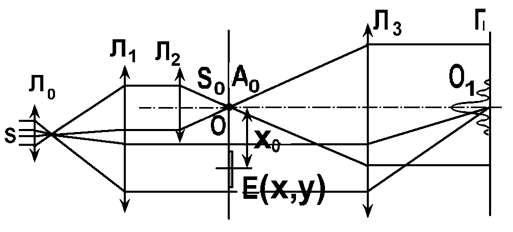Рис. 3.5.2. Схема получения голограммы Фурье.

Выберем в плоскости П систему координат Оху, а в плоскости Г - систему О1х1у1. Расположим начала координат этих систем на оптической оси линзы Л3. Точечный опорный источник S0 поместим в начало координат системы Оху. Комплексное световое поле, образованное источником S в плоскости фотопленки, обозначим двумерной функцией h(x,y). Комплексное световое поле в плоскости Г обозначим через g(x1,y1). Линза Л3 выполняет над функцией h(x,y) двумерное преобразование Фурье, так что функции h(x,y) и g(x1,y1) связаны следующей зависимостью:

(3.5.5)

где l - длина волны когерентного света источника S, f1 - фокусное расстояние линзы Л3. Запишем (3.5.5) в несколько иной форме:

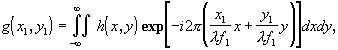(3.5.6)

из которой видно, что в подынтегральном выражении роль пространственных частот играют величины

(3.5.7)

Иначе:

(3.5.8)

Таким образом,

(3.5.9)

где H(p,q) - двумерное преобразование Фурье функции h(x,y), а p и q определяются равенствами (3.5.7). Будем называть H(p,q) комплексным спектром функции h(x,y), а его составляющие A(p,q) и  в соответсвии с выражением

- амплитудным и фазовым спектрами.

Вернемся к схеме рис. 3.5.2 и составим выражение для функции h(x,y). Как видно из рисунка, эта функция образуется двумя компонентами: полем опорного источника и полем, прошедшим пленку с изображением объекта. Так как мы рассматриваем опорный источник в виде идеальной точки, обозначим его поле с помощью двумерной дельта- функции Дирака с амплитудой волны А0, т.е.

(3.5.10)

Поле центрированного объекта обозначим через Е0(х,у). Ввиду того, что в принятой схеме объект смещен относительно начала координат на величину х0 и у0, то поле будет характеризоваться функцией Е0(х-х0, у-у0)=Е(х,у). Таким образом, получим:

(3.5.11)

Поле в плоскости Г определим в соответствии с выражением (3.5.8). Как известно, преобразование Фурье суммы функций равно сумме преобразований Фурье слагаемых, поэтому получим комплексные спектры слагаемых в (3.5.11) раздельно. Для первого слагаемого, вспоминая, что по одному из определений дельта- функции

получим:

(3.5.12)

Для второго слагаемого

Делая подстановку

получим

или

(3.5.13)

где  - комплексный спектр центрированного объекта.

Таким образом, учитывая, что

из (3.5.12) и (3.5.13) получим:

(3.5.14)

Комплексный спектр  центрированного объекта через амплитудный и фазовый спектры выразится следующим образом:

Поэтому для поля (3.5.14) будем иметь:

(3.5.15)

Голограмма получается регистрацией поля в плоскости Г на фотопленку. Ввиду того, что фотографическая эмульсия реагирует на интенсивность света I(p,q), прозрачность пленки t (p,q) (амплитудное пропускание) является функцией интенсивности:

, (3.5.16)

где g - коэффициент контрастности пленки. Коэффициент k определяется чувствительностью фотослоя и временем экспозиции.

Интенсивность светового поля в плоскости Г равна квадрату модуля функции g(x₁,y₁), т.е.

(3.5.17)

где

а звездочкой обозначена комплексно сопряженная величина. Подставив в (3.5.17) вместо g(x1,y1) ее значение из (3.5.15), получим:

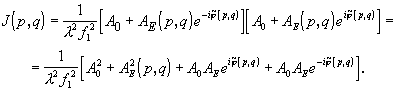(3.5.18)

Здесь

(3.5.19)

Учитывая, что , получим:

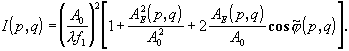(3.5.20)

Функцию прозрачности голограммы получим, подставив (3.5.20) в (3.5.16). При А0, достаточно больших по сравнению с АЕ(p,q), разлагая (3.5.16) в степенной ряд и ограничиваясь линейным приближением, получим:

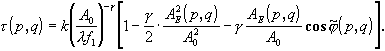(3.5.21)

Запишем полученное выражение в более удобной для анализа форме:

(3.5.22)

Здесь

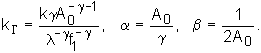
Соотношение (3.5.22) является уравнением голограммы Фурье, полученной по схеме рис. 3.5.2. но представляет собой связь амплитудного пропускания t (p,q) голограммы с пространственно-частотными характеристиками голографируемого плоского предмета.

С точностью до разрешающей способности фотопленки и в пределах линейности ее характеристики на голограмме зафиксирована вся информация о предмете, содержащаяся в его амплитудном AE(p,q) и фазовом j E(p,q) спектрах. Для сведения к минимуму нелинейных искажений при формировании голограммы необходимо правильно выбирать входящие в уравнение параметры kG , a и b , а следовательно, и определяющие их амплитуду А0 опорного пучка и коэффициент контрастности g . Обычно принимают А0>10AE и g » 2.

Проанализируем уравнение голограммы (3.5.22).

В правой части уравнения содержится три слагаемых. Постоянная составляющая kG a =t 0 определяет среднюю прозрачность голограммы, которая получилась бы в случае перекрывания пучка от предмета, т.е. когда AE(p,q)=0.

Вторая составляющая kG b AE2(p,q) характеризует дополнительную неравномерную засветку голограммы пучком от предмета. Так как эта составляющая вычитается из t 0, то она уменьшает прозрачность голограммы, особенно в тех местах, где велико значение амплитудного спектра предмета. Ввиду того, что для большинства предметов наибольшую энергию несут низкочастотные составляющие спектра, потемнение голограммы Фурье за счет второй составляющей сосредоточено вблизи начала координат частотной плоскости.

Вторая составляющая содержит лишь часть информации о предмете, так как в ней отсутствует фазовый спектр. Полную информацию содержит третья составляющая, возникающая благодаря интерференции предметного пучка с опорным. Из-за наличия в ней функции  она знакопеременная. При положительном значении косинуса она уменьшает прозрачность голограммы, при отрицательном- увеличивает. Эта составляющая представляет собой косинусную волну, промодулированную по амплитуде и фазе. Вектор несущей частоты косинусоиды имеет составляющие

(3.5.23)

зависящие от смещения предмета относительно опорного источника. Направление фронта волны косинусоиды получим из соотношения (3.5.19) для фазы. Полагая j E(p,q)=0, из (3.5.19) получим:

(3.5.24)

Так как фронт волны соединяет точки с одинаковой фазой, то, положив

(3.5.25)

получим уравнение фронта косинусоиды:

Это прямая, имеющая наклон k=-y0/x0. Косинусная волна на голограмме проявляется в виде периодических интерференционных полос и особенно хорошо видна при равномерных AE(p,q) и j E(p,q), т.е. когда она не сильно искажена модуляцией.

Таким образом, объект на голограмме представляется в виде суперпозиции элементарных косинусоид. Этим и объясняется, почему этот способ записи получил название голографии Фурье.

Следует отметить, что фазовый спектр j E(p,q), входящий в выражение для  есть фазовый спектр центрированного объекта, ибо смещение объекта на величины х0 и у0 от центра учитывается первым слагаемым в (3.5.19). Поэтому для всех объектов, имеющих центральную симметрию (двумерный аналог четности функций), j E(p,q)=0.

Отметим также, что голограмма Фурье любого вещественного объекта имеет центральную симметрию. Это следует из того, что уравнение голограммы таких объектов инвариантно по отношению к перемене знака пространственных частот, ибо входящие в него члены AE(p,q) и  не изменяют знака при изменении знаков p и q, первый вследствие центральной симметрии, а второй - вследствие четности.

При восстановлении голограммы она освещается параллельным пучком света (рис. 3.5.3) Каждая косинусоидальная решетка при этом сформирует изображение соответствующей точки в бесконечности. Если же сразу за голограммой установить линзу, то изображения всех точек пернесутся из бесконечности в фокальную плоскость линзы. Изображение объекта и сопряженное ему изображение будут располагаться симметрично относительно оси. На оси будет располагаться светлое пятно, обусловленное наличием первых двух слагаемых в уравнении голограммы.
 

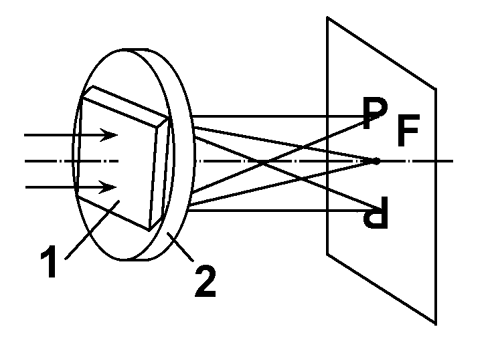Рис. 3.5.3. Восстановление голограммы Фурье: 1-голографическая фотопластинка; 2-линза.

Изложенные выше свойства голограмм играют важную роль при разработке методов оптической фильтрации, краткая характеристика которых приведена в следующем параграфе.

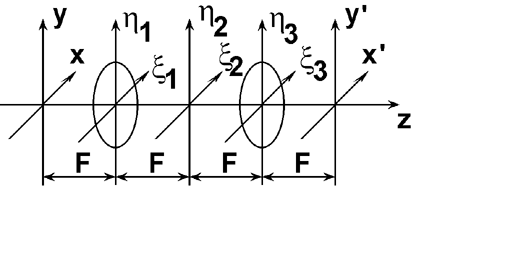
Сначала входной сигнал (x,y) подвергается Фурье-преобразованию линзой 1. Световое поле в плоскости (x2,h 2) распределено в соответствии со спектром сигнала S(fx,fy)

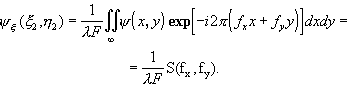(3.6.1)

Здесь мы воспользуемся тем, что x 2=l Ffx, h 2=l Ffy.

Сигнал y x (x 2,h 2), пропорциональный спектру S(fx,fy), подвергается аналогичному преобразованию Фурье при прохождении через линзу 2. Тем самым в плоскости изображений распределение поля будет иметь вид

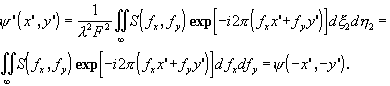(3.6.2)

Таким образом, система 4-F восстанавливает в плоскости изображений входной сигнал в перевернутом виде.

Систему 4-F можно с успехом использовать для пространственной фильтрации. Для этого в плоскости (x 2,h 2) помещают пространственный фильтр. Если фильтр имеет модуляционную характеристику T(x 2,h 2), то после прохождения фильтра спектр S(fx,fy) входного сигнала принимает вид

(3.6.3)

При этом в плоскости изображений будет формироваться сигнал , соответствующий спектру . Тем самым, меняя модуляционную характеристику фильтра, можно обеспечить требуемое преобразование оптического пространственного сигнала.

Пространственная фильтрация широко используется для решения задач, связанных с проблемой распознавания образов. Предположим, что на входе системы 4-F помимо полезного сигнала присутствуют посторонние сигналы (помехи)  и

(3.6.4)

Тогда в спектральной плоскости будет формироваться сумма спектров:

(3.6.5)

Если в спектральной плоскости расположить фильтр с модуляционной характеристикой

(3.6.6)

то сразу за ним спектр сигнала  принимает вид

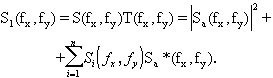(3.6.7)

Волновой фронт поля  в плоскости (x 2,h 2) является плоским, поэтому, проходя через линзу 2, это световое поле должно фокусироваться в точку на плоскости изображения. Второе слагаемое в (3.6.7) представляет поле не с плоским фронтом, его преобразование линзой 2 дает на выходной плоскости некоторое распределенное изображение.

Пространственный фильтр, превращающий парциальную световую волну, несущую информацию о полезном сигнале, в плоскую волну, называют согласованным с полезным (распознаваемым) сигналом.

Если во входной волне содержится полезный сигнал, то присутствие в системе согласованного фильтра приводит к появлению в выходной плоскости яркой светящейся точки. Фиксируя появление этой точки, можно регистрировать наличие на входе системы распознаваемого сигнала.

где

а опорной волной - волна

где

Рассчитаем модуляционную характеристику голограммы

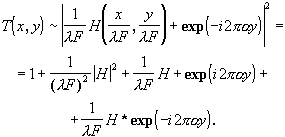(3.6.8)

В случае использования этой голограммы в качестве пространственного фильтра для некоторого входного сигнала существенным является наличие в характеристике (3.6.8) третьего и четвертого членов. Они действуют как пространственные фильтры Н и Н*. Их действие приводит к тому, что после второго Фурье-преобразования в выходной плоскости системы (рис.3.6.1) будут присутствовать сигналы

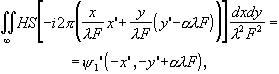(3.6.9)

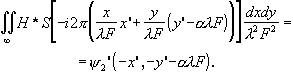(3.6.10)

Из выражений (3.6.9) и (3.6.10) видно, что выходной сигнал, полученный при использовании фильтра Н, будет сдвинут вверх по вертикали на расстояние , сигнал же, полученный при использовании фильтра Н*, будет на то же расстояние сдвинут вниз. Таким образом появляется возможность рассматривать эти сигналы порознь.
 

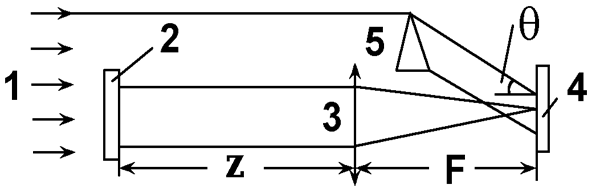Рис. 3.6.2. Схема Ван дер Люгта для синтеза пространственных фильтров.

Рассмотренный голографический метод получения пространственных фильтров снимает проблему синтеза оптических масок в пространстве частот. Трудности же синтеза оптических масок в пространстве координат менее серьезны, поскольку требуемые переходные функции (импульсные отклики), как правило, имеют простую форму и необходимые маски с пропусканием h(x ,h ) несложно изготовить с помощью простых фотографических средств.

Синтезирование пространственных фильтров голографическими методами позволяет успешно решать важную в практическом отношении задачу улучшения качества оптических изображений, выполняемого уже после того, как получено изображение. Такая задача относится к задачам, связанным с апостериорной ("послеопытной") обработкой информации.

Пусть некоторая оптическая система формирует изображение интересующего нас объекта. Идущая от объекта световая волна может рассматриваться как входной сигнал y (x,y), а изображение объекта - как выходной сигнал y '(x',y'). Если бы система не вносила искажений, то имело бы место равенство y=y '. Однако в реальной ситуации следует считаться с тем, что любая система вносит определенные искажения, которые описываются некоторой переходной функцией (или передаточной функцией Н). С помощью голографических методов можно синтезировать пространственный фильтр с модуляционной характеристикой H*. Совмещая его с фильтром, синтезированным обычным фотоспособом, получим составной фильтр с модуляционной характеристикой

(3.6.11)

Для апостериорной обработки искаженного сигнала y ' воспользуемся схемой 4-F (рис.3.6.1) В ее входной плоскости разместим искажение y ', а в спектральной плоскости разместим фильтр с модуляционной характеристикой (3.6.11). Тогда в выходной плоскости системы 4-F сформируется сигнал . Так как S'=SH, то согласно (3.6.11)

(3.6.12)

Это означает, что  Таким образом, благодаря модуляционной характеристике (3.6.11) фильтр "учел" и автоматически "вычел" те искажения, которые оптическая система внесла при построении изображения.

Когерентная оптическая фильтрация зарекомендовала себя удобным средством обработки изображений, что объясняется ее высоким быстродействием, двумерностью, а также относительной универсальностью, поскольку могут быть реализованы почти любые линейные пространственно-инвариантные операции фильтрации над комплексными сигналами. Тем не менее когерентные методы имеют и слабые стороны. К ним, в первую очередь, относится требование когерентности источника света, что не позволяет обрабатывать самосветящиеся объекты, такие, например, как изображения на телевизионном экране. Другим недостатком когерентных систем является их большая чувствительность к различного рода шумам (например, связанным с зернистостью фотоэмульсий, дефектами оптических поверхностей и т.д.). Эти шумы негативно сказываются на качестве выходных изображений.

Указанные недостатки методов обработки информации в когерентном свете стимулируют разработку альтернативных способов, основанных на принципах некогерентной оптики. Однако, поскольку подробное изучение этих способов выходит за рамки книги, ограничимся самыми общими замечаниями.

В отличие от когерентного оптического сигнала y (x,y) некогерентный сигнал  описывается не комплексной, а действительной функцией. Информация содержится в интенсивности световой волны

(3.7.1)

Фазовая информация в световой волне утрачивается.

Интеграл свертки примет вид

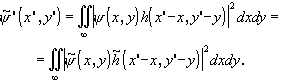(3.7.2)

Здесь функция

(3.7.3)

является некогерентной функцией системы. Аналогично в случае некогерентных изопланарных систем вводят некогерентную передаточную функцию системы

(3.7.4)

Используя (3.7.3) и известную в Фурье-анализе теорему автокорреляции, можно построить выражение

(3.7.5)

которое определяет связь между передаточными функциями для когерентного и некогерентного сигналов.

В заключение данной главы рассмотрим дополнительно вопрос о количественных характеристиках качества изображений формируемых оптическими системами.

Если бы волновой интервал светового излучения был бесконечно мал, а оптическая система (объектив) совершенна, то функция y 0(x,y) преобразовалась бы идеальным образом в распределение освещенности y '0(x',y'); единственным различием их было бы линейное увеличение. Реальное же распределение освещенности в изображении y 'i(x',y') отличается от идеального y 0 из-за поперечного дифракционного рассеяния света, а так же несовершенств объектива. Качество изображения - мера степени отличия y i от y 0.

Принято использовать три параметра для сравнения распределений в объекте (предмете) и изображении. Этими параметрами являются:

относительное содержание (емкость) структуры TL

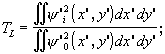(3.8.1)

правдоподобие изображения ФL

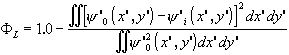(3.8.2)

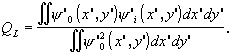(3.8.3)

Пределы интегрирования здесь формально , но обычно достаточно интегрировать в пределах формата данного изображения. Заметим, что

(3.8.4)

Относительное содержание структуры наиболее близко подходит к тому, что обычно подразумевается под качеством изображения; реально же величина TL представляет искажения вариаций функции y 0 в процессе ее регистрации. Ограничения применимости величины TL связаны с искажениями, вносимыми оптической системой или приемником изображения. Величина TL также "не чувствительна" к искажениям координатной сетки из-за дисторсии. Эти искажения хорошо описываются величиной ФL - поэтому она широко используется в приложениях, где подобие координатной сетки принципиально важно. Корреляционное качество отражает сочетание требований как к подобию координатной сетки, так и к структурному содержанию изображения.

Параметры качества представляют собой удобные оценочные характеристики для случаев, когда параметры поверхности предмета априорно хорошо известны; указанные параметры - одночисловые, они легко сравнимы (для разных систем) и непосредственно взаимосвязаны (для данной системы).

• 1. Гудмен Дж. Введение в фурье-оптику. - М.: Мир, 1970, 364 с.
• 2. Дьяков В.А., Тарасов Л.В. Оптическое когерентное излучение.- М.: Советское Радио, 1974; 169 c.
• 3. Парыгин В.Н., Балакший В.И. Оптическая обработка информации.-М.: Изд. МГУ, 1987, 141 c.
• 4. Матвеев А.Н. Оптика.- М.: Высшая школа, 1985, 351c.
• 5. Марешаль А., Франсон М. Структура оптического изображения.- М.: Мир, 1964. 295 с.
• 6. Козанне А., Флере Ж., Мэтр Г., Руссо М. Оптика и связь.- М.: Мир, 1984, 504 c.
• 7. Франсон М. Голография.- М.: Мир, 1972, 246 с.
• 8. Сороко Л.М. Основы голографии и когерентной оптики.- М.: Наука, 1971, 616 с.
• 9. Федоров Б.Ф. Эльман Р.И. Цифровая голография. - М.: Наука, 1976, 152 с.
• 10. Уэзерелл У. Оценка качества изображения. //Сб. Проектирование оптических систем. Под ред. Р. Шеннона и Дж. Вайнта.-М.: Мир, 1983, 430 с.