Термин "компьютерная оптика" является относительно новым и не приобрел еще строгого определения. Разные авторы очень часто вкладывают в него различное содержание. Можно сказать, что в самом широком смысле слова "компьютерная оптика" - это компьютеры в оптике и оптика в компьютерах. Сюда относятся численные решения задач дифракции и фокусировки излучения, автоматизированное проектирование и гибкое автоматизированное производство оптических систем, обработка изображений, оптический вычислительный эксперимент, оптические процессоры и запоминающие устройства, цифровая голография.
Очень часто формулировка предмета компьютерной оптики как научного направления сужается и в нее вкладывается более конкретный смысл. При этом считается, что компьютерная оптика - это получение на основе применения ЭВМ оптических элементов, осуществляющих требуемое преобразование волновых полей. Именно на такую направленность компьютерной оптики и сориентирован, в основном, материал настоящей главы.
Компьютерная оптика возникла на стыке физической оптики и информатики и стала формироваться как новое научное направление, объединяющее теорию, методы и технические средства обработки оптических сигналов с использованием ЭВМ, и отражающее тот факт, что современная оптика и оптические приборы становятся все в большей степени цифровыми.
Какие качественно новые свойства придают компьютеры оптическим системам? Главных свойств два. Во-первых, это способность к адаптации и гибкость в перенастройке. Благодаря тому, что компьютер способен перестраивать структуру обработки сигнала без перестройки своей физической структуры, он является идеальным средством адаптивной обработки оптических сигналов и быстрой перестройки ее на решение разных задач. Здесь речь идет прежде всего об информационной адаптации. Заметим попутно, что эта способность ЭВМ к адаптации и перестройке нашла также применение в активной и адаптивной оптике для управления световыми пучками как переносчиками энергии.
Во-вторых, это простота и естественность получения и переработки количественной информации, содержащейся в оптических сигналах, соединение оптических систем с другими информационными системами. Цифровой сигнал, представляющий в компьютере оптический сигнал,- это переносимая оптическим сигналом информация, так сказать, в чистом виде, лишенная своей физической оболочки.
Благодаря универсальному характеру цифровой сигнал представляет собой идеальное средство объединения различных информационных систем. Теоретической базой компьютерной оптики являются теории информации, цифровой обработки сигналов, статистических решений, теория систем и преобразований в оптике.
Одно из основных предназначений компьютерной оптики состоит в расширении гаммы конструктивных элементов оптических систем. Помимо традиционных линз, призм и зеркал с помощью современных вычислительных средств и систем управления могут быть созданы оптические элементы с более широкими функциональными возможностями. Типичным представителем семейства элементов компьютерной оптики является плоский оптический элемент - киноформ. Сочетание киноформных корректоров с обычными линзами позволяет проектировать оптические системы со слабыми сферическими аберрациями и новыми оптико-физическими свойствами.
Существо подхода к созданию элементов компьютерной оптики состоит в следующем. Оптический элемент, работающий на пропускание или на отражение излучения, характеризуется амплитудно-фазовой функцией пропускания или отражения. Эта характеристика должна быть определена, исходя из решаемой задачи преобразования волнового поля. Для простейших случаев может быть известно ее аналитическое выражение, например, фазовая функция сферической или цилиндрической линзы. В общем же случае требуется применение ЭВМ для определения характеристики оптического элемента. При этом ЭВМ может использоваться как для численных расчетов в рамках прямой задачи, так и для решения обратных задач. Таким образом, на этапе проектирования, компьютер используется для определения характеристики создаваемого оптического элемента.
После того, как указанная характеристика сформирована в памяти ЭВМ, возникает задача переноса ее на физическую среду с помощью программно-управляемого технологического автомата. На этом этапе роль компьютера также очень велика.
Созданный оптический элемент необходимо далее экспериментально исследовать и аттестовать. Экспериментальные данные при этом регистрируются, как правило, в виде различного рода распределений интенсивности света: теневых картин, интрферограмм, голограмм. При этом компьютер необходим для обработки, отображения и интерпретации экспериментальных данных, поскольку визуальные наблюдения и ручная обработка не позволяют получать количественные результаты.
Необходимо отметить, что в компьютерной оптике перспективным методом исследования является вычислительный эксперимент, в котором ключевую роль играет компьютер. Процесс создания элементов компьютерной оптики носит сложный итерационный характер и на компьютер возлагается также функция обеспечения диалога с проектировщиком, технологом и исследователем.
В компьютерной оптике можно выделить следующие основные направления:
Цифровой голографией называется метод получения и восстановления голограмм, при котором основная роль отводится компьютеру. Роль компьютера заключается в расчете распределения коэффициента прозрачности или преломления по полю голограммы, которое затем записывается в оптической запоминающей среде. С помощью компьютера рассчитывается и восстанавливается изображение, которое записано на такой синтезированной голограмме и которое можно было бы получить оптическим путем.
Имеется ряд веских оснований для такого синтеза голограмм и, в частности, то обстоятельство, что геометрические размеры голографического объекта в этом случае не ограничиваются такими факторами, как когерентность освещения, вибрация или турбулентность воздуха, и появляется возможность исследовать путем моделирования некоторые голографические эффекты.
Еще более существенным моментом, стимулирующим синтезирование голограмм с помощью компьютеров, является возможность создать оптический волновой фронт для такого объекта, который физически не существует. Потребность в формировании волнового фронта, соответствующего объекту, определяемому расчетным путем, возникает в любом случае, когда требуется визуально отобразить в трех измерениях результаты того или иного трехмерного исследования, например, при моделировании разрабатываемых конструкций. Иногда волновой фронт от синтезированной голограммы может служить интерференционным эталоном для контроля сложной оптической поверхности в процессе ее обработки. Другая область применения таких голограмм связана с экспериментами по пространственной фильтрации. В некоторых случаях изготовить фильтр с заданной функцией оптическими методами бывает затруднительно, в то же время компьютер решает подобные задачи сравнительно легко.
Для того, чтобы получить синтезированную голограмму, поступают следующим образом:
1) Задавшись объектом, голограмму которого нужно получить, рассчитывают с помощью компьютера комплексную амплитуду испускаемого им света в плоскости, находящейся на определенном расстоянии от него. Эта плоскость будет плоскостью голограммы.
2) Рассчитанная таким образом комплексная амплитуда кодируется так, чтобы она была действительной и положительной функцией. Например, производят сложение амплитуды света, испускаемого объектом, с какой-нибудь комплексной амплитудой, которая играет роль когерентного фона. Результирующая интенсивность будет в этом случае действительной и положительной функцией.
3) Соответствующее устройство, управляемое компьютером, изображает графически распределение значений этой функции в некоторой плоскости. Это может быть, например, электронно-лучевая трубка, печатающее устройство и т.п.
4) Полученный чертеж фотографируется; негатив и представляет собой синтетическую голограмму. Для того, чтобы голограмма хорошо дифрагировала свет, нужно, чтобы структура чертежа была достаточно тонкой. Поэтому обычно фотографируют чертеж со значительным уменьшением.
Для формирования голограммы применяются компьютерные дисплеи, штриховые печатающие устройства, плоттеры. Этап фотографического уменьшения, разумеется, может быть исключен, если применить специальные выходные устройства, позволяющие осуществить непосредственную запись голограммы требуемого размера. Быстродействие современных компьютеров достаточно для расчета синтетической голограммы, идентичной голограмме, полученной при записи интерференционной картины, созданной реальным объектом. Тем не менее, в большинстве случаев рассчитываются голограммы, где отсутствуют полутона и вся голограмма состоит из светлых участков (апертур) на черном фоне. Такая голограмма называется бинарной. Бинарную голограмму с помощью компьютера можно рассчитать и построить в увеличенном масштабе за несколько минут.
Фотографическое уменьшение и репродуцирование бинарных голограмм легче и более точно, чем серых голограмм. На качество бинарной голограммы совершенно не влияют нелинейные фотографические эффекты, поэтому в процессе фотоуменьшения бинарных голограмм требуется значительно менее строгий контроль величины экспозиции и режима проявления.
Другое преимущество бинарной голограммы в сравнении с серой голограммой состоит в том, что она направляет на восстанавливаемое изображение большую часть из падающего на нее света. Если в обычной голограмме светоотдача, или эффективность, равна 6,2%, то светоотдача бинарной голограммы достигает 10%. Помимо более высокой светоотдачи преимущество бинарной голограммы состоит в том, что при восстановлении возникает меньше шумов от света, рассеянного зернистой структурой фотоэмульсии. Бинарная голограмма может быть вычерчена плоттером. Восстановленное с бинарной голограммы в когерентном свете изображение имеет все свойства изображения, получаемого с обычной голограммы.
Бинарные голограммы являются эффективным промежуточным звеном, позволяющим осуществлять связь между цифровой и оптической формами представления информации. Один из методов цифровой голографии позволяет получать голограммы, которые при восстановлении падающий на голограмму свет направляют на создание одного изображения, т.е. имеют эффективность около 100%.
Рассмотрим более подробно процедуру получения цифровой голограммы. Сделаем
это на примере голограммы Фурье, принцип регистрации которой был рассмотрен
в параграфе 3.5.2. Как
и всякие другие цифровые модели, цифровые модели голограмм воспроизводят
процесс лишь приближенно, однако наиболее существенные свойства, подлежащие
исследованию, представляются четко выделенными, в явном виде, что часто
нельзя сделать в реальном процессе. Одно из основных приближений связано
с переходом от непрерывных величин к дискретным, с которыми работает ЭВМ.
Этот переход, уменьшая точность результатов, в то же время не вносит принципиальных
изменений в процесс, так как с уменьшением шага дискретизации модель все
более приближается к непрерывной. Степень такого приближения ограничена
лишь возможностями ЭВМ. Кроме того, есть разумный предел плотности дискретизации,
определяемый разрешающей способностью оптических элементов и фотоматериалов,
участвующих в голографическом процессе. Этот предел для функций с ограниченным
спектром определяется известной специалистам теоремой Котельникова, из
которой следует, что если функция имеет спектр, ограниченный частотой f0,
то она может быть представлена с большой точностью в точках xm, отстоящих
одна от другой на расстоянии ![]() .
Теорема Котельникова легко распространяется на двумерные функции. В этом
случае отсчеты берут в узлах прямоугольной сетки с размерами ячеек
.
Теорема Котельникова легко распространяется на двумерные функции. В этом
случае отсчеты берут в узлах прямоугольной сетки с размерами ячеек
![]() .
.
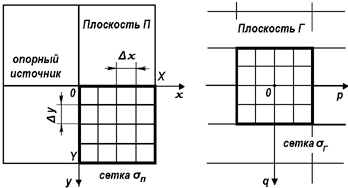
Итак, переходя к цифровому моделированию голографического процесса, заменим части плоскостей П и Г (см. рис. 3.5.2), ограниченные прямоугольными апертурами, сетками. В узлах этих сеток зададим отсчеты поля. Эти сетки в плоскости предметов обозначим s П, а в плоскости голограммы - s Г . Для удобства последующих преобразований расположение сеток в плоскостях П и Г выберем таким, как показано на рис. 4.2.1. Правомерность такого выбора будет видна из дальнейшего. Чтобы параметры сеток отвечали теореме Котельникова, необходимо выполнение следующих соотношений:
 |
|
| Рис. 4.2.1 Расположение сеток. |
При этом суммарное число узлов сетки s П равно MN. Перейдем в плоскости П к новым координатам. Приняв размеры сетки Х=У=1, получаем:
![]() . (4.2.2)
. (4.2.2)
Следовательно, координаты узлов сетки s П выразятся так:
![]() (4.2.3)
(4.2.3)
Число узлов сетки s Г выбирают так, чтобы было обеспечено взаимно однозначное соответствие между изображениями, заданными на s П и его дискретным преобразованием Фурье, заданным на s Г. Это число узлов также оказывается равным MN. Последнее определено тем, что в системе, состоящей из MN точек, полной является система тригонометрических функций с частотами
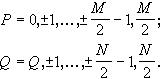 (4.2.4)
(4.2.4)
Соотношения между размерами сеток s П
и s Г получим из (4.2.1)
с учетом того, что ![]() и
и ![]() согласно (3.5.7)
согласно (3.5.7)
![]() (4.2.5)
(4.2.5)
Выбор сеток в плоскостях П и Г означает, что все непрерывные функции в этих плоскостях могут быть представлены своими дискретными значениями в узлах сетки. Эти значения теперь являются функциями номеров узлов, т.е. m и n в плоскости П, p и q в плоскости Г. Для отличия от непрерывных величин аргументы дискретных величин будем обозначать индексами, например Еmn, вместо Е(хm,уn), Аpq вместо А(р,q). Установим соответствие между основными физическими величинами, рассмотренными ранее, и их цифровыми моделями. Поле в плоскости П представим так:
![]() (4.2.6)
(4.2.6)
дискретное преобразование Фурье от hmn определит соотношение:
![]() (4.2.7)
(4.2.7)
Примем c учетом (4.2.6)
![]() (4.2.8)
(4.2.8)
Цифровая модель голограммы Фурье, являющаяся аналогом ранее рассмотренной модели (3.5.22), будет иметь вид
![]() (4.2.9)
(4.2.9)
где
![]() (4.2.10)
(4.2.10)
Величину ![]() можно интерпретировать
как коэффициент двойного ряда Фурье от дискретной функции, заданной на
двумерном интервале MN
можно интерпретировать
как коэффициент двойного ряда Фурье от дискретной функции, заданной на
двумерном интервале MN![]() . При
этом в уравнении голограммы последнее слагаемое является не чем иным, как
косинусным коэффициентом Фурье
. При
этом в уравнении голограммы последнее слагаемое является не чем иным, как
косинусным коэффициентом Фурье ![]() изображения предмета. С учетом изложеного уравнение цифровой голограммы
Фурье, удобное для расчетов на ЭВМ, принимает вид:
изображения предмета. С учетом изложеного уравнение цифровой голограммы
Фурье, удобное для расчетов на ЭВМ, принимает вид:
![]() (4.2.11)
(4.2.11)
Здесь в общем случае имеем
![]() (4.2.12)
(4.2.12)
![]() (4.2.13)
(4.2.13)
![]() (4.2.14)
(4.2.14)
В двух первых формулах последние члены в прямоугольных скобках используются при наличии рассеивателя со случайной фазой. Если рассеиватель не используют, то они равны нулю и формула упрощается.
При компьютерном расчете структуры голограммы исходной информацией является
изображение, которое разбивают на отдельные участки в соответствии с выбранной
сеткой (т.е. из изображения делают выборку значений Еmn в узлах сетки),
а также задаваемые параметры M, N, kГ, ![]() .
В результате расчета должны быть получены величины
.
В результате расчета должны быть получены величины ![]() прозрачности голограммы в узлах сетки
прозрачности голограммы в узлах сетки ![]() Г.
Г.
Основой вычисления является выполнение дискретного преобразования Фурье (ДПФ), причем двумерное преобразование выполняется в два этапа: сначала по строкам, а затем по столбцам. Последовательность вычислений показана на рис. 4.2.2. Для выполнения одномерных преобразований используется алгоритм быстрого преобразования Фурье (БПФ).
В приложении 1 содержится краткое описание процедур ДПФ и БПФ, которые
широко вошли в практику компьютерных расчетов. Для удобства вычислений
матрицу ![]() , полученную после
преобразования строк, транспонируют и повторное преобразование также выполняют
по строкам. В результате двойного БПФ получают коэффициенты
, полученную после
преобразования строк, транспонируют и повторное преобразование также выполняют
по строкам. В результате двойного БПФ получают коэффициенты ![]() и
и ![]() по которым и определяют
значения
по которым и определяют
значения ![]() . Результаты вычислений
вместе с заданными параметрами используют для расчета прозрачности голограммы
по ее формуле. Эти значения и выдает машина.
. Результаты вычислений
вместе с заданными параметрами используют для расчета прозрачности голограммы
по ее формуле. Эти значения и выдает машина.
Отпечатанную цифровую голограмму затем фотографируют с соответствующим
уменьшением и используют для восстановления
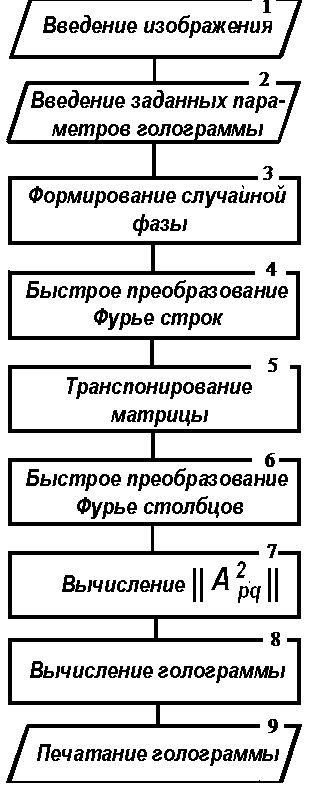 |
| Рис. 4.2.2 Последовательность вычислений
голограммы Фурье |
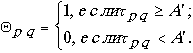 (4.2.17)
(4.2.17)
В данном случае 1 соответствует уровню белого, а 0 - черного. Окончательно получим
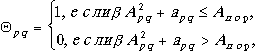 (4.2.18)
(4.2.18)
![]()
![]()
В выборе параметров b и ![]() имеется определенный произвол. В общем случае их увеличение приводит к
снижению доли высоких пространственных частот в голограмме. Сама же двоичная
голограмма в большой степени подчеркивает высокие пространственные частоты.
имеется определенный произвол. В общем случае их увеличение приводит к
снижению доли высоких пространственных частот в голограмме. Сама же двоичная
голограмма в большой степени подчеркивает высокие пространственные частоты.
Процесс изготовления киноформа выглядит следующим образом.
На компьютере рассчитываются дискретные значения фазы ![]() объектной световой волны. Полученные значения фазы обрабатываются таким
образом, чтобы их отклонения от начальной фазы лежали в интервале от 0
до 2p радиан по всей области выборки, т.е. из
каждого значения фазы вычитаются величины, кратные 2p
радианам. В результате получается двумерный массив, состоящий из дискретных
значений фазы
объектной световой волны. Полученные значения фазы обрабатываются таким
образом, чтобы их отклонения от начальной фазы лежали в интервале от 0
до 2p радиан по всей области выборки, т.е. из
каждого значения фазы вычитаются величины, кратные 2p
радианам. В результате получается двумерный массив, состоящий из дискретных
значений фазы
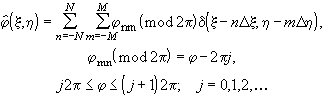 (4.2.19)
(4.2.19)
Данный массив кодируется массивом значений яркости в многоградационной шкале, который уже отображается в виде картины на выходное устройство компьютера, например на дисплей. Полученная картина фотографируется с необходимым уменьшением и конечный фотоснимок отбеливается в дубящем отбеливателе. При отбеливании градации фотографического почернения превращаются в соответствующее распределение значений оптической толщины. Полученный таким образом киноформ имеет функцию пропускания
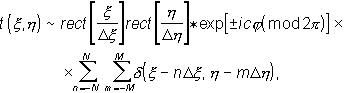 (4.2.20)
(4.2.20)
Знак показателя экспоненциального сомножителя определяется тем, что используется в качестве киноформа- негатив или позитив фотоснимка картины киноформа. Соответственно и изображение, восстанавливаемое киноформом, будет мнимым или действительным.
Из рассмотрения функции пропускания киноформа (4.2.20) следует,
что для восстановления исходного волнового фронта без искажений необходимо,
чтобы константа с равнялась единице. Это означает, что свет, падающий
на участок с фазой ![]() , будет
задерживаться ровно на одну длину волны по сравнению со светом, падающим
на участок с фазой
, будет
задерживаться ровно на одну длину волны по сравнению со светом, падающим
на участок с фазой ![]() . Если
такое согласование фаз было достигнуто, то весь свет, падающий на киноформ,
будет участвовать в формировании единственного (действительного или мнимого)
изображения записанного обекта. В противном случае киноформ подобен осевой
голограмме, в которой действительное и мнимое изображения частично накладываются;
часть света дифрагирует в нулевой порядок, создавая яркое пятно в центре
изображения. Качество изображения резко ухудшается. На практике согласование
фаз достигается путем тщательного контроля процессов экспонирования и проявления
уменьшенных фотоснимков киноформа, а также отбеливания.
. Если
такое согласование фаз было достигнуто, то весь свет, падающий на киноформ,
будет участвовать в формировании единственного (действительного или мнимого)
изображения записанного обекта. В противном случае киноформ подобен осевой
голограмме, в которой действительное и мнимое изображения частично накладываются;
часть света дифрагирует в нулевой порядок, создавая яркое пятно в центре
изображения. Качество изображения резко ухудшается. На практике согласование
фаз достигается путем тщательного контроля процессов экспонирования и проявления
уменьшенных фотоснимков киноформа, а также отбеливания.
Допустим, что монохроматическое поле, несущее информацию об исследуемом
объекте, было зарегистрировано в двух плоскостях: в плоскости изображения
и в фурье-плоскости. Будем считать, что поле зависит только от одной пространственной
координаты. Обозначим поле в плоскости изображения через ![]() ,
в фурье-плоскости - через
,
в фурье-плоскости - через ![]() .
Для операции преобразования Фурье введем символ
.
Для операции преобразования Фурье введем символ
![]() (4.3.1)
(4.3.1)
так что
![]() (4.3.2)
(4.3.2)
Пусть при регистрации поля получена информация о функциях a(x)
и A(x), а информация о фазовых множителях отсутствует. Задача состоит
в построении комплексной функции по заданному ее модулю и модулю ее фурье-образа.
Для решения этой задачи была предложена итерационная процедура, которая
заключалась в следующем. В качестве пробной функции бралась функция, модуль
которой совпадал с заданным в плоскости изображения модулем a(x),
а фазовый множитель ![]() брался
произвольным; в работе он строился с помощью генератора случайных чисел.
Пробную функцию удобно обозначить через y0(x),
в дальнейшем индекс будет совпадать с числом выполненных итераций, перед
началом итераций имеем
брался
произвольным; в работе он строился с помощью генератора случайных чисел.
Пробную функцию удобно обозначить через y0(x),
в дальнейшем индекс будет совпадать с числом выполненных итераций, перед
началом итераций имеем
![]() (4.3.3)
(4.3.3)
Для этой функции строилось ее преобразование Фурье
![]() (4.3.4)
(4.3.4)
Затем у полученной функции модуль заменялся на правильный, т.е. на A(x), а фаза сохранялась. Так получали функцию в фурье-плоскости
![]() (4.3.5)
(4.3.5)
что можно представить как
![]() (4.3.6)
(4.3.6)
Затем выполнялось обратное преобразование Фурье и снова исправлялся модуль, при этом получалась функция в плоскости изображения в первом приближении
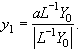 (4.3.7)
(4.3.7)
На следующем шаге выполнялись такие же преобразования. Всю итерационную процедуру можно представить формулами
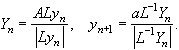 (4.3.8)
(4.3.8)
Если процесс окажется сходящимся, то функцию, получающуюся в качестве предела итераций, будем обозначать через y
![]() (4.3.9)
(4.3.9)
Описанный алгоритм расчета распределения фазы известен в литературе
как алгоритм Гершберга-Сэкстона Практика его использования показала, что
во многих случаях процесс действительно сходился, и функция y совпадала
с исходным комплексным полем ![]() .
Несмотря на то, что в настоящее время разработан ряд более совершенных
и корректных методов решения фазовой проблемы алгоритм Гершберга-Сэкстона
остается одним из самых популярных.
.
Несмотря на то, что в настоящее время разработан ряд более совершенных
и корректных методов решения фазовой проблемы алгоритм Гершберга-Сэкстона
остается одним из самых популярных.
Если задана фазовая функция оптического элемента, то в принципе всегда можно решить прямую задачу дифракции волн на оптическом элементе и получить распределение поля в интересующей нас области. Сложнее обстоит дело с решением обратной задачи.
Для уяснения физической сущности проблемы рассмотрим рис. 4.3.1.
Плоский оптический элемент Ф, расположенный в области G плоскости
u=(u,v), освещается пучком Е монохроматического излучения
длины волны. Требуется сформировать в области D плоскости х=(х,у)
волновое поле I(x,z). Фазовая функция оптического элемента полностью
определяет поведение пучка за плоскостью u и, в частности, в интересующей
нас области х. Задача состоит в отыскании фазовой функции оптического
элемента (u,y), обеспечивающего формирование волнового поля. С математической
точки зрения обратная задача является некорректной: во-первых, решение
может вообще не существовать; во-вторых, оно может быть неоднозначным;
в-третьих, оно может быть неустойчивым.
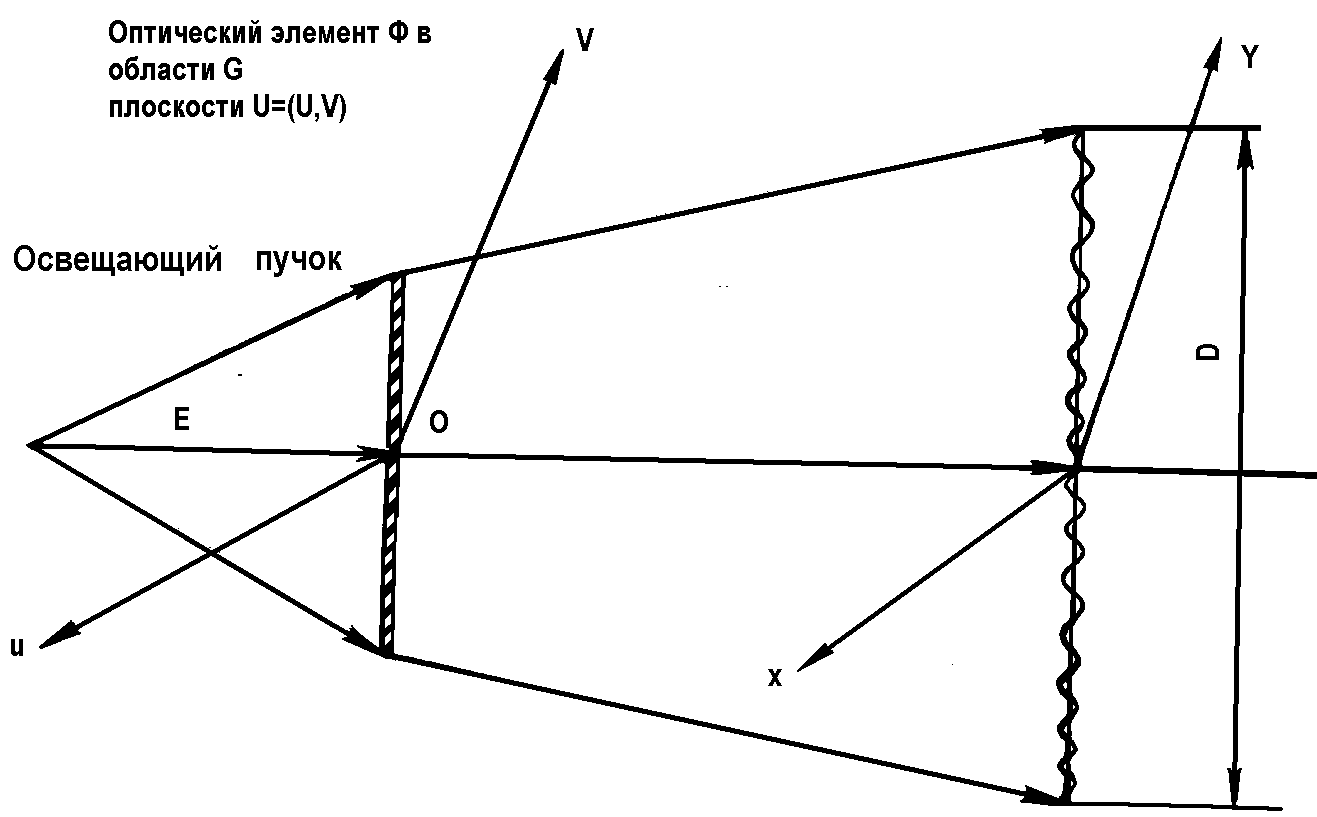 |
| Рис. 4.3.1 Постановка задачи формирования оптического поля. |
Отсуствие решения, как правило, обусловлено ограничениями, налагаемыми на область фокусировки фундаментальными физическими законами. Например, хорошо известно, что нельзя получить в области фокусировки пятно, диаметр которого D меньше, чем дифракционный предел, определяемый поперечным размером d линзы (фокусатора), длиной волны и фокусным расстоянием f, то есть Df/d. Аналогичные ограничения накладываются на минимально достижимую толщину линии при фокусировке в отрезок на плоскости, перпендикулярной оси распространения. Решение задачи фокусировки может отсутствовать не только по причине противоречия законам дифракции. В случае, когда область фокусировки не расположена в плоскости перпендикулярной оптической оси, а является, например, трехмерной пространственной кривой, вполне определенные ограничения накладываются из-за того, что в силу закона прямолинейного распространения света перенос энергии осуществляется вдоль оптической оси. Нельзя, в частности, требовать, чтобы при фокусировке в тонкий цилиндр, расположенный вдоль оптической оси, энергия целиком была сосредоточена в нем, а интенсивность вне тонкого цилиндра равнялась нулю. Ясно, что энергия к более удаленным от фокусатора точкам цилиндра переносится через периферийные области пространственных сечений, более близких к фокусатору.
Успехи в решении обратных задач привели к качественному обновлению элементной базы современных оптических систем. Так, имеются практические достижения в создании киноформных линз большой светосилы. Сообщается о создании "безаберрационных" объективов, содержащих несколько киноформных линз и обладающих прекрасными массогабаритными характеристиками. Наконец, есть несомненные достижения в области создания различных типов фокусаторов. В самом широком смысле термин "фокусатор" используется среди специалистов для обозначения элементов компьютерной оптики, обеспечивающих концентрацию световой энергии в пределах пространственной области с заранее заданной пространственной конфигурацией. Чаще всего речь идет о фокусировке излучения в некоторую фокальную кривую с заданным распространением интенсивности на ней. Зачем нужны фокусаторы? Прежде всего для лазерных технологических установок в промышленности и медицине. Лазер без фокусатора - это только генератор излучения, лазер с фокусатором - это уже компонент гибкой производственной системы с программируемым режимом технологических операций. Но производство - не единственная область применения фокусаторов излучения. Закон пространственного распределения энергии в фокальной области оптической системы определяет режим нагрева мишеней при лазерном управляемом термодинамическом синтезе, течение химических реакций, стимулированных лазерным излучением. В оптическом приборостроении часто требуется сложная форма фокальной кривой.
На сегодняшний день созданы фокусаторы излучения в видимом и инфракрасном диапазонах с регулировкой интенсивности вдоль фокальной линии. Эти результаты являются наглядной иллюстрацией достижений компьютерной оптики.
Огромные возможности открывает компьютерная оптика для получения оптических элементов, позволяющих корректировать амплитудно-фазовое распределение поля в световых пучках. Такого рода корректоры позволяют сформировать волновой фронт заданной формы. К числу корректоров принадлежат, в частности, компенсаторы- элементы, преобразующие плоский или сферический волновой фронт в асферический произвольного порядка. Основное назначение компенсаторов - контроль оптических поверхностей. При этом компенсатор формирует эталонный волновой фронт для интерферометрического исследования изготавливаемой оптической поверхности или же играет роль "нулевой линзы", сводя асферическую задачу к сферической.
Как следует из выражения (3.2.2), фазовая функция сферической линзы в параксиальном приближении имеет вид
![]() , (4.3.10)
, (4.3.10)
где F - фокусное расстояние; D - диаметр линзы; ![]() .
.
Приведение фазовой функции (4.3.10) к интервалу [0, 2p ) показано на рис. 4.3.2.
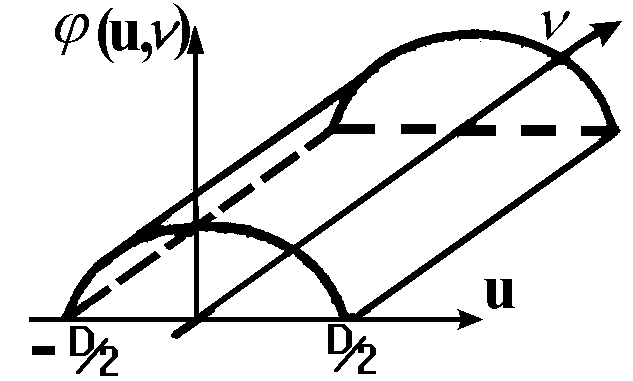
![]()
и имеет порядок длины волны. Высота микрорельефа определяется по формуле
![]() (4.3.11)
(4.3.11)
Радиусы зон Френеля можно найти из соотношения
![]() ,
,
откуда следует
![]() (4.3.12)
(4.3.12)
Число полных зон j0 на линзе определяется
из условия ![]() и удовлетворяет
соотношению
и удовлетворяет
соотношению
![]() , (4.3.13)
, (4.3.13)
где ![]() - означает целую
часть числа с округлением в меньшую сторону.
- означает целую
часть числа с округлением в меньшую сторону.
Рассмотрим цилиндрическую линзу (рис. 4.3.3), описываемую фазовой функцией
![]() . (4.3.14)
. (4.3.14)
Приведение фазовой функции к интервалу [0, 2p ) аналогично проведенному выше для сферической линзы. Границы зон в данном случае - прямые линии, а расстояния между ними определяются формулой (4.3.12) при замене rj на x j. На рис. 4.3.4 приведен фотошаблон плоской цилиндрической линзы.
Рассмотрим призму с углом a (рис. 4.3.5).
Призма обеспечивает фазовый сдвиг, линейно зависящий от координаты, и характеризуется фазовой функцией
![]() , (4.3.15)
, (4.3.15)
где ![]() .
.
Приводя фазовую функцию ![]() к интервалу [0, 2p ) (см. рис. 4.3.6)
получим 1-D дифракционную решетку "с блеском" (рис. 4.3.7).
к интервалу [0, 2p ) (см. рис. 4.3.6)
получим 1-D дифракционную решетку "с блеском" (рис. 4.3.7).
Максимальная высота рельефа:
![]()
и уравнение высоты микрорельефа имеет вид
![]() . (4.3.16).
. (4.3.16).
Различным углам отклонения b соответствуют различные периоды решетки
![]() , (4.3.17),
, (4.3.17),
где ![]() .
.
Бинарная 1-D амплитудная дифракционная решетка получается при
замене линейно-меняющейся фазовой функции в пределах одного периода на
двоичную функцию, принимающую значения ± p
/2 (рис. 4.3.8).
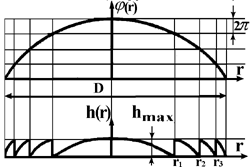 |
| Рис. 4.3.3 Цилиндрическая линза. |
 |
| Рис. 4.3.4 Фотошаблон плоской цилиндрической линзы. |
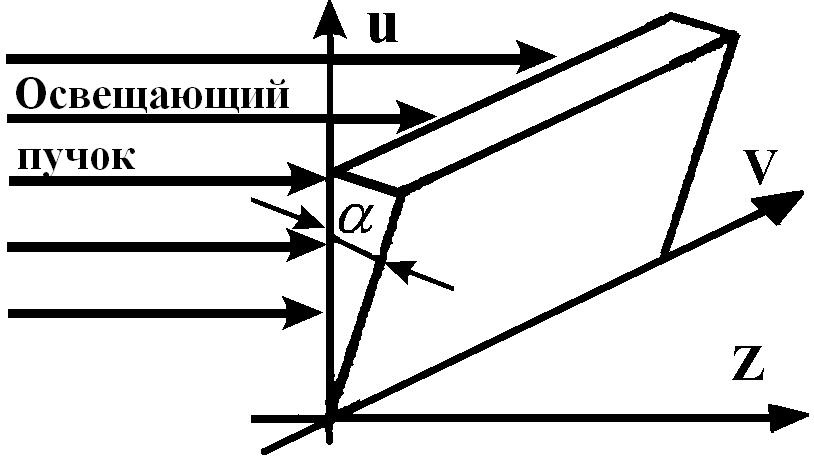 |
| Рис. 4.3.5 Призма. |
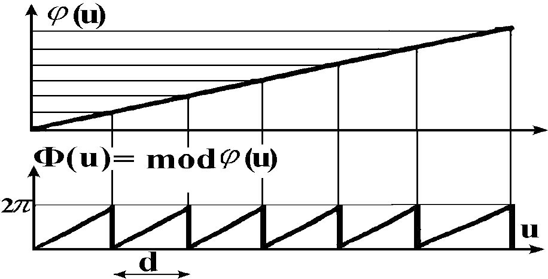 |
| Рис. 4.3.7 Фазовая функция дифракционной решетки "с блеском". |
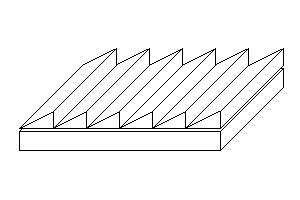 |
| Рис. 4.3.7 Дифракционная решетка "с блеском" |
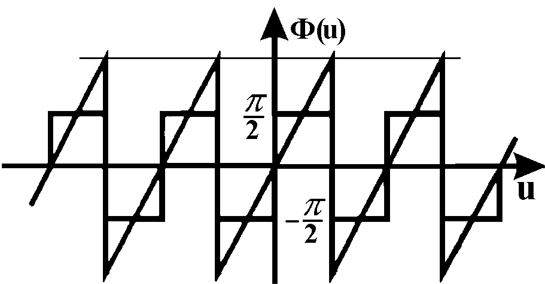 |
| Рис. 4.3.8 Сравнение бинарной дифракционной решетки и решетки "с блеском". |
Альтернативным техническим решением по отношению к плоским дифракционным элементам киноформного типа является использование гибких управляемых зеркал, поверхность которых может принимать ту или иную форму в зависимости от управляющих напряжений, приложенных к зеркалу. Гибкое зеркало, управляемое ЭВМ, позволяет по заданной программе изменять интенсивность в зоне фокусировки.
Задача расчета формы поверхности гибкого зеркала имеет особенности.
Функцию ![]() , описывающую профиль
зеркала, к которому приложены управляющие воздействия aj,
можно представить в виде:
, описывающую профиль
зеркала, к которому приложены управляющие воздействия aj,
можно представить в виде:
где ![]() - функции отклика
зеркала, зависящие от конструкции и технологии его изготовления. Функциия
отклика
- функции отклика
зеркала, зависящие от конструкции и технологии его изготовления. Функциия
отклика ![]() описывает форму
поверхности зеркала при единичном управляющем воздействии, приложенном
к j-му приводу. При этом, естественно, предполагается линейность
отклика. Расчет требуемого профиля поверхности зеркала сводится к определению
конечного числа управляющих воздействий {aj}.
описывает форму
поверхности зеркала при единичном управляющем воздействии, приложенном
к j-му приводу. При этом, естественно, предполагается линейность
отклика. Расчет требуемого профиля поверхности зеркала сводится к определению
конечного числа управляющих воздействий {aj}.
Общая схема гибкого зеркала мембранного типа приведена на рис. 4.3.9 (патент фирмы "Perkin-Elmer").
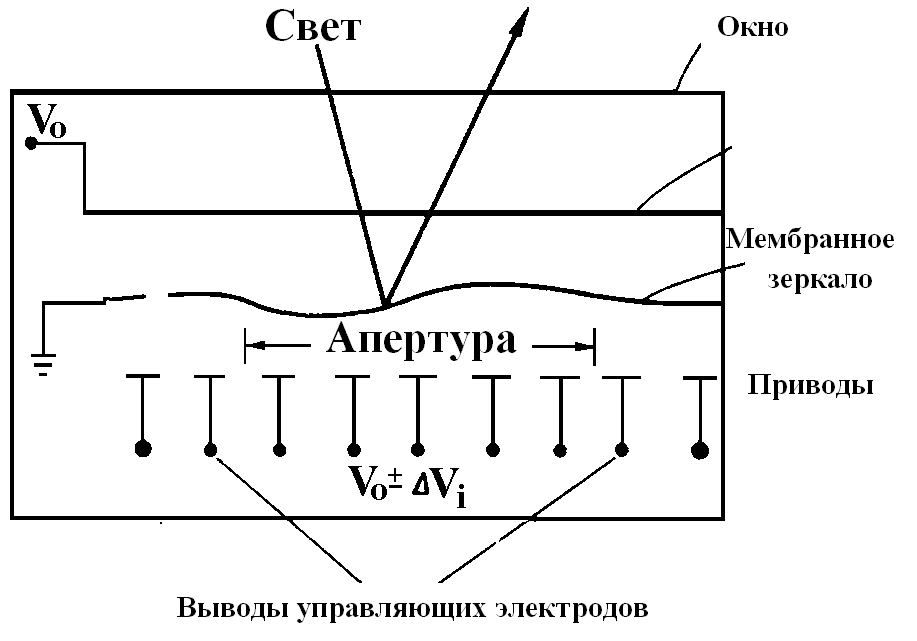 |
| Рис. 4.3.9 Схема управляемого зеркала мембранного типа |
 |
| Рис. 4.3.10 Общий вид зеркала мембранного типа. |
Перспективным представляется создание комбинированных формирующих оптических элементов, состоящих из киноформа и гибкого зеркала. Эти элементы удачно дополняют друг друга. Гибкое зеркало позволяет создать сравнительно плавную оптическую поверхность с нужной глубиной рельефа Задача киноформного элемента - обеспечить требуемое пространственное разрешение при сравнительно небольшой глубине рельефа. Число зон при этом становится небольшим, и эффективность киноформа повышается (меньше сказывается пространственная дискретизация фазовой функции). Кроме того, комбинированный оптический элемент позволяет в некоторой степени скорректировать небольшие отклонения параметров формирующей системы от расчетных (например, ввести коррекцию угла падения излучения на элемент, расстояния до плоскости фокусировки, ширины светового пучка на элементе и т.д.).
Очень часто излучение, идущее от фокусатора, достигает заданного объекта, пройдя через область пространства с нестационарной случайно-неоднородной средой. В этом случае эффективно реализовать фокусирующие свойства гибкого зеркала можно лишь перманентно меняя форму его отражающей поверхности с целью компенсации влияния неоднородностей. Как известно, оптические элементы, характеристики которых могут под воздействием управляющих сигналов изменяться во времени, составляют элементную базу адаптивной оптики. Таким образом, проблема создания фокусаторов, способных работать в условиях случайных помех, оказывается тесно связанной с необходимостью использования методов адаптивной оптики. Среди этих методов важную роль играет метод фазового сопряжения.
Метод фазового сопряжения следует из принципа оптической обратимости.
В приближении геометрической оптики его можно сформулировать так: если
волну ![]() , прошедшую участок
с неоднородным показателем преломления, послать обратно по тому же самому
пути, заменив фазу этой волны j на u=-j
, то на выходе из среды волна восстановит свой первоначальный неискаженный
фазовый профиль. Замена фазы j на -j
эквивалентна операции сопряжения комплексной амплитуды волны:
, прошедшую участок
с неоднородным показателем преломления, послать обратно по тому же самому
пути, заменив фазу этой волны j на u=-j
, то на выходе из среды волна восстановит свой первоначальный неискаженный
фазовый профиль. Замена фазы j на -j
эквивалентна операции сопряжения комплексной амплитуды волны: ![]() .
Этим объясняется название метода фазового сопряжения. Рис. 4.4.1
иллюстрирует сказанное.
.
Этим объясняется название метода фазового сопряжения. Рис. 4.4.1
иллюстрирует сказанное.
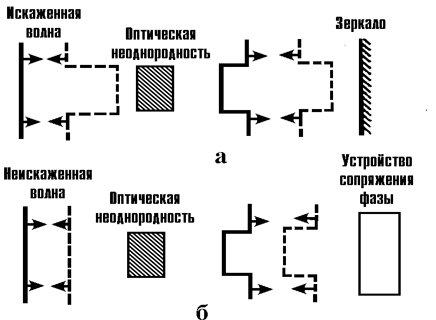 |
| Рис. 4.4.1 Компенсация возмущающего фактора оптической неоднородности. |
Пусть плоская волна проходит участок оптически неоднородной среды, например кусок стекла. В результате фаза волны искажается и на выходе из среды приобретает характерную впадину (сказалось относительное увеличение оптической длины пути и времени распространения волны через стекло). При отражении от обычного зеркала запаздывание на особом участке сохраняется и при повторном прохождении фазовая неоднородность удваивается (рис. 4.4.1, а). Для того чтобы скомпенсировать первоначальное отставание по фазе при обратном распространении, необходимо обратить фазу, т.е. сформировать волну с профилем фазы -j . Фаза этой волны на месте впадины имеет выступ, равный ей по значению (рис. 4.4.1, б). Этот особый участок теперь уже опережает по фазе остальные. После повторного прохождения волной неоднородности опережающий участок отстанет по фазе ровно настолько, чтобы скомпенсировать введенное возмущение. Волна в результате двукратного распространения останется плоской (рис. 4.4.1, б).
Рассмотрим реализацию идеи фазового сопряжения на примере фокусатора, использующего для коррекции фазы гибкое зеркало (рис. 4.4.2).
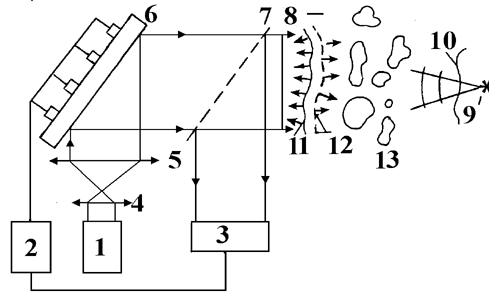 |
| Рис. 4.4.2 Оптическая фокусирущая система, реализующая принцип фазового сопряжения. 1- лазер; 2-ЭВМ; 3- датчик волновогво фронта; 4, 5 - линзы телескопа; 6- мембранное зеркало; 7 - ответвлитель; 8 - начальный фронт волны; 9 - мишень; 10 - фронт в области мищени; 11 - фронт отраженной волны; 12 -скоректированный фронт; 13 - фронт неоднородности |
Световой пучок от лазера 1, пройдя формирующий телескоп, образованный линзами 4 и 5, и отразившись от гибкого зеркала 6, выходит из системы, имея изначально плоский волновой фронт 8. Пройдя область со случайными неоднородностями (в частности, это может быть турбулентная атмосфера) вблизи мишени 9 волна будет иметь значительно возмущенный фронт 10. Часть энергии, отразившись от мишени в виде сферической волны, которая в данной оптической системе будет играть роль опорного пучка. К фокусатору этот пучок подойдет с сильно искривленным волновым фронтом 11. Степень отклонения этого фронта от фронта плоской волны определяется от датчика фазы 3, излучение на который подается при помощи светоделительной пластины 7. Датчик фазы, представляющий собой
Рассмотрим реализацию идеи фазового сопряжения на примере фокусатора, использующего для коррекции фазы гибкое зеркало (рис. 4.4.2).
Световой пучок от лазера 1, пройдя формирующий телескоп, образованный линзами 4 и 5, и отразившись от гибкого зеркала 6, выходит из системы, имея изначально плоский волновой фронт 8. Пройдя область со случайными неоднородностями (в частности, это может быть турбулентная атмосфера) вблизи мишени 9 волна будет иметь значительно возмущенный фронт 10. Часть энергии, отразившись от мишени в виде сферической волны, которая в данной оптической системе будет играть роль опорного пучка. К фокусатору этот пучок подойдет с сильно искривленным волновым фронтом 11. Степень отклонения этого фронта от фронта плоской волны определяется от датчика фазы 3, излучение на который подается при помощи светоделительной пластины 7. Датчик фазы, представляющий собой интерферометрическое или голографическое устройство, регистрирует фазовый профиль, пришедшей от мишени волны. Поступающая от датчика фазы информация перерабатывается ЭВМ 2 и в виде управляющих сигналов подается на гибкое зеркало. Это приводит к формированию на выходе фокусатора волны с обращенным (фазово-сопряженным) по отношению к опорному пучку фронтом 12. При распространении этой волны фазовые неоднородности будут компенсироваться. В результате излучение полностью сфокусируется на мишени.
Оптические элементы этого класса позволили решить целый ряд практически
интересных задач, связанных с задачами анализа и формирования поперечно-модового
состава лазерного излучения. Как известно, каждой моде соответствует известная
математическая функция двух переменных. Многомодовое излучение падает на
транспарант, пропускание которого определяется функцией ![]() .
Компьютер формирует в своей памяти двумерный массив чисел, соответствующих
моде с номером k, а фотопостроитель переводит числа в значения оптической
плотности на фотоматериале. В результате получаем набор плоских оптических
элементов, соответствующих различным модовым функциям. Используя их как
оптические элементы, можно построить прибор для анализа и формирования
поперечно-модового состава излучения. Рассмотрим принцип действия анализатора.
Многомодовое излучение падает на транспарант, пропускание которого определяется
функцией
.
Компьютер формирует в своей памяти двумерный массив чисел, соответствующих
моде с номером k, а фотопостроитель переводит числа в значения оптической
плотности на фотоматериале. В результате получаем набор плоских оптических
элементов, соответствующих различным модовым функциям. Используя их как
оптические элементы, можно построить прибор для анализа и формирования
поперечно-модового состава излучения. Рассмотрим принцип действия анализатора.
Многомодовое излучение падает на транспарант, пропускание которого определяется
функцией ![]() . Интенсивность
света в фокусе выходной линзы при этом равна интенсивности k-й моды. Меняя
транспаранты, можно измерить интенсивность различных мод и таким образом
решить задачу определения поперечного состава. На практике на одном оптическом
элементе с использованием голографического метода можно записать сразу
несколько модовых функций. При освещении такого транспаранта многомодовым
излучением одномоментно в различных точках фокальной плоскости линзы измеряется
интенсивность различных мод. Описанный оптический элемент подобен дифракционной
решетке, разделяющей по углам излучение различных длин волн. Однако в данном
случае решается гораздо более серьезная задача: по углам разделяются поперечно-модовые
составляющие излучения. Имея набор оптических элементов, согласованных
с модовыми функциями, можем решить также и задачу формирования требуемого
поперечно-модового состава лазерного излучения. Как практически использовать
выше означенные возможности? Поскольку при распространении излучения в
волоконном световоде (ВОЛС) поперечно-модовая структура его обладает устойчивостью,
имеется возможность уплотнить канал передачи информации. Для этого нужно
использовать в качестве переносчиков сообщения колебания, соответствующие
различным поперечным модам. Число одновременно возбуждаемых на входе ВОЛС
колебаний может составлять от нескольких единиц до нескольких десятков.
Каждое колебание-переносчик несет свое сообщение и распространяется по
волоконному световоду независимо от других переносчиков. На выходе ВОЛС
проводится анализ поперечно-модового состава излучения и индивидуальная
демодуляция сообщения в каждой из выделяемых мод. Пропускная способность
ВОЛС при модовом уплотнении резко возрастает. При этом усложнение аппаратуры
связи, особенно на приемном конце, не очень существенно.
. Интенсивность
света в фокусе выходной линзы при этом равна интенсивности k-й моды. Меняя
транспаранты, можно измерить интенсивность различных мод и таким образом
решить задачу определения поперечного состава. На практике на одном оптическом
элементе с использованием голографического метода можно записать сразу
несколько модовых функций. При освещении такого транспаранта многомодовым
излучением одномоментно в различных точках фокальной плоскости линзы измеряется
интенсивность различных мод. Описанный оптический элемент подобен дифракционной
решетке, разделяющей по углам излучение различных длин волн. Однако в данном
случае решается гораздо более серьезная задача: по углам разделяются поперечно-модовые
составляющие излучения. Имея набор оптических элементов, согласованных
с модовыми функциями, можем решить также и задачу формирования требуемого
поперечно-модового состава лазерного излучения. Как практически использовать
выше означенные возможности? Поскольку при распространении излучения в
волоконном световоде (ВОЛС) поперечно-модовая структура его обладает устойчивостью,
имеется возможность уплотнить канал передачи информации. Для этого нужно
использовать в качестве переносчиков сообщения колебания, соответствующие
различным поперечным модам. Число одновременно возбуждаемых на входе ВОЛС
колебаний может составлять от нескольких единиц до нескольких десятков.
Каждое колебание-переносчик несет свое сообщение и распространяется по
волоконному световоду независимо от других переносчиков. На выходе ВОЛС
проводится анализ поперечно-модового состава излучения и индивидуальная
демодуляция сообщения в каждой из выделяемых мод. Пропускная способность
ВОЛС при модовом уплотнении резко возрастает. При этом усложнение аппаратуры
связи, особенно на приемном конце, не очень существенно.
Теперь уместным будет обсудить физический смысл поперечно-модовых разложений излучения и ответить на вопрос: "Являются ли поперечные моды выдумкой математиков или же действительно излучение в неоднородной среде состоит из множества мод?"
Аналогичный вопрос ставился в дискуссии о природе белого света: "В самом деле в солнечном свете есть монохроматические волны различного цвета или мы только математически выражаем этот процесс суммой синусоид?" Современная точка зрения на последний вопрос состоит в том, что спектральное разложение приобретает конкретный физический смысл при взаимодействии излучения со спектральным прибором. В этом случае оно оказывается физически адекватным представлением, соответствующим сущности физической задачи. Точно так же и разложение излучения по модам становится физически адекватным и целесообразным при взаимодействии излучения с анализатором мод. Примечательно, что этот шаг удалось сделать только на основе применения компьютера.
В природе нам не известны генераторы эталонных поперечных мод, подобные генераторам монохроматического излучения. Отсутствуют также оптические элементы, подобные призмам и дифракционным решеткам, но предназначенные для проведения поперечно-модового анализа. Таким образом, компьютерная оптика восполняет существенный пробел путем создания искуcственных эталонов физических величин по их математическим моделям. Вполне возможно, что в дальнейшем будут открыты новые физические явления и созданы соответствующие приборы без применения компьютеров. Однако, это уже ни в коей мере не повлияет на оценку роли компьютерной оптики в задаче анализа и формирования поперечно-модового состава излучения.
Важнейшей задачей оптики всегда было повышение качества и информационной производительности оптических приборов. В настоящее время современная оптико-электронная техника, по существу, решила проблему формирования изображений высокого качества и большой информационной емкости для большинства практических задач. Важнейшей стала проблема эффективности использования заключенного в них огромного объема информации, т.е. проблема обработки изображений, голограмм и интерферограмм.
Фундаментальным методом решения этой проблемы является развитие на основе теории информации и теории сигналов информационных аспектов теории оптического изображения, оптических систем и привлечение современных методов обработки сигналов, из которых важнейшими в настоящее время являются средства компьютерной техники. Оптические приборы с вычислительными устройствами теперь усиливают не только оптические свойства зрения, но и его аналитические возможности. Это привело к тому, что в рамках общего научного направления обработки оптических полей сформировалась еще одна дисциплина, называемая иконикой. В настоящее время иконика объединяет теоретические и экспериментальные исследования, направленные на всестороннее изучение свойств изображений в "тесной увязке" их со зрительным восприятием.
Техническое обеспечение процедуры компьютерной обработки оптических полей помимо персональных и специализированых компьютеров включает сканеры, ПЗС-матрицы, телекамеры и т.п. На начальных этапах компьютерная оптика заимствовала эти устройства из других областей, таких как машинная графика и автоматизированное проектирование. Но в последнее время стали создаваться и получили широкое распространение специализированные технические средства компьютерной оптики, среди которых особое место занимают параллельные процессоры для обработки многомерных сигналов.
Cинтез изображений по сигналам, получаемым с датчиков физических полей. Это задача цифровой обработки сигналов датчиков, направленная на их преобразование в форму, пригодную для визуализации. Сюда, например, относится томографический синтез, цифровое восстановление акустических и радиоголограмм, формирование изображений в оптических и других системах с кодированной апертурой и т.д.
Коррекция искажений. Это задача компьютерной обработки искаженного изображающей системой или датчиком изображения или сигнала, направленная на получение изображения (сигнала), соответствующего выходу идеальной изображающей системы. Такова, например, обработка изображения для повышения его резкости и подавления случайных помех.
Препарирование изображений. Идеальная изображающая система не обязательно дает изображение, наилучшим образом отвечающее требованиям конкретной задачи визуального анализа и выделения информации, поскольку требования к идеальным характеристикам практически являются компромиссом между требованиями широкого класса задач. Для отдельных конкретных задач могут потребоваться дополнительные преобразования сигнала, облегчающие визуальный анализ путем подчеркивания одних особенностей и деталей изображения и устранения других, изменения пространственных соотношений, измерения и визуализации количественных характеристик и т.п. Такие преобразования, являющиеся инструментом визуального анализа изображений профессиональным пользователем-экспертом в конкретной области применения данной визуальной информации, и называются препарированием изображения. Существенная особенность препарирования изображения - диалоговый режим обработки под управлением и наблюдением пользователя, неформализованный опыт и знания которого как бы включаются при этом в систему обработки.
Характерной особенностью препарирования изображения является также то, что в работу пользователю-эксперту предлагается для сравнительного анализа не само исходное (скорректированное) изображение, а варианты в виде цветных, стереоскопических, подвижных (анимационные) изображений объекта исследования по результатам выявления существенных признаков.
Кодирование изображений. Это вид обработки, при котором осуществляется преобразование оптических сигналов и изображений в форму, удобную для передачи по каналам связи и архивного хранения. Важной составной частью кодирования является, в частности, сжатие данных, т.е. кодирование, снижающее требования к пропускной способности каналов связи и емкости запоминающих устройств.
Измерение изображений полей. Под этой задачей подразумевается обработка оптических сигналов, в результате которой получаются количественные данные, предназначенные для принятия решений и управления автоматическими исполнительными механизмами.
Последний тип обработки оптических полей является необходимым атрибутом различных автоматизированных измерительных систем. Ниже в качестве примера рассматривается одна из таких систем, программное обеспечение которой было разработано на кафедре оптики и спектроскопии физического факультета МГУ с целью обработки изображений лазерных пучков со сложной пространственной структурой.
Важнейшим элементом УВИ является камера с матричным фотоприемником. Фотоприемник представляет собой матрицу полупроводниковых элементов, работающих на принципе зарядовой связи (ПЗС-матрица). Снимаемое с каждого элемента напряжение линейно зависит от его освещенности, то есть от интенсивности соответствующего участка падающего излучения.
При "считывании" напряжения с каждого элемента матрицы на выходе приемника формируется последовательность электрических сигналов, в которой закодировано распределение интенсивности. Для оцифровки сигналов от камеры в данной системе применяется компьютерная плата "Видеопорт-2", позволяющая фиксировать процессы длительностью приближенно 20 мс. Время ввода оцифрованного сигнала в компьютер зависит только от быстродействия последнего. Программа ввода и первичной обработки изображений с применением платы "Видеопорт-2" работает под управлением операционной системы MS-DOS и позволяет вводить и сохранять на диске компьютера черно-белые изображения размером до 512* 512 точек с цветовым разрешением до 64 градаций яркости.
 |
| Рис. 4.6.1 Схема регистрации излучения ПЗС-матрицей. |
ПЗС-матрица выполнена на полупроводниковой подложке n-типа нанесением металлических электродов с изоляцией от полупроводника тонким слоем диэлектрика.
Принцип работы ПЗС-матрицы демонстрирует рис. 4.6.1. Если на электрод подается отрицательное напряжение, то на поверхности полупроводника формируется обедненный слой, в котором нет свободных зарядов, способных перемещаться. Фактически обедненный слой представляет собой потенциальную яму, в которой могут накапливаться неосновные носители заряда из числа носителей, возникающих под действием света.
Передача заряда осущестляется под действием приложенного к управляющим
контактам напряжения трехфазного сигнала. Сначала, как показано на рис.
4.6.1,а, накапливаются дырки в потенциальной яме, созданной высоким
отрицательным напряжением, приложенным к контакту 1.
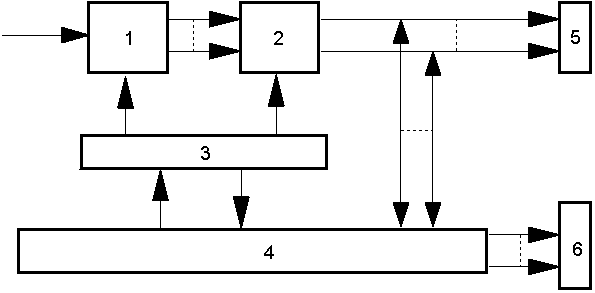 |
| Рис. 4.6.2 Блок-схема устройства для обработки видеосигнала. 1- АЦП; 2- буфер; 3- генератор; 4- схема управления и адресации; 5,6- шина данных и адресная шина компьютера. |
Если теперь приложить высокое отрицательное напряжение к контакту 2, то потенциальная яма углубится в сторону этого контакта, и туда же переместятся дырки (рис. 4.6.1,б). Сразу же конфигурацию потенциальных ям приводят к виду, показанному на рис. 4.6.1,в. Затем следует новый цикл. При повторении циклов заряд последовательно перемещается и воспринимается как изменяющийся во времени сигнал, несущий информацию об интенсивности и пространственном распределении излучения.
Помимо ПЗС-матрицы в УВИ входит еще несколько электронных узлов системы "Видеопорт-2", обеспечивающих в определенном режиме считывание и оцифровку видеосигналов и их ввод в память компьютера. Эти узлы и их функциональные связи в упрощенном виде изображены на рис. 4.6.2. Сигналы с камеры попадают в 6-разрядный аналогово-цифровой преобразователь (АЦП) 1, что позволяет получать до 64 градаций яркости. Оцифрованные данные накапливаются в буфере 2. В нем каждой точке изображения соответствует одна ячейка, а каждой строке изображения - строка матрицы. Такое построение упрощает схему управления, так как переключение осуществляется по строчным синхроимпульсам (ССИ). По кадровым синхроимпульсам (КСИ) происходит опознание начала кадра.
Генератор формирует сигналы оцифровки для АЦП, сигналы записи-чтения для блока памяти, импульсы переключения для устройства адресации.
Схема адресации и управления опознает начало кадра, начало строки и, соответственно, управляет работой генератора и буфера.
Устройство работает в двух режимах: режим записи сигнала в буфер и режим передачи содержимого в компьютер.
При помощи компьютера можно управлять такими параметрами изображения, как контрастность и яркость, изменяя опорное напряжение на АЦП и постоянную составляющую сигнала соответственно.
Полученная информация о видеосигнале хранится и обрабатывается в виде массива с размерностью, зависящей от выбранного формата ввода (количества точек по вертикали и по горизонтали), элементами которого являются целые числа от 0 до 255. Меньшие значения соответствуют темным, а большие- светлым областям изображения.
Автоматизированная измерительная система имеет развитое программное обеспечение (ПО). Пользователю предлагается обширное меню, включающее проведение целого ряда операций над структурой оптического изображения и вычислений его характеристик. Все управление работой УВИ и ходом операций осуществляется с клавиатуры ПК или манипулятором "мышь". Все предлагаемые процедуры обработки изображений можно разбить на две группы. К первой относятся операции изменения яркости и контрастности изображений, а также проведение бинаризации и просмотр отдельных структурных фрагментов. Чаще всего указанные операции осуществляются на предварительной стадии обработки оптических полей. Ко второй группе относятся операции, обеспечивающие определение характеристик оптических полей. С их помощью определяются следующие характеристики.
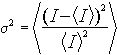 , (4.6.1)
, (4.6.1)
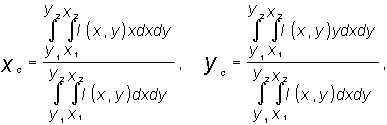 (4.6.2)
(4.6.2)
Двумерный коэффициент автокорреляции интенсивности:
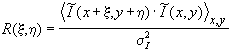 , (4.5.3)
, (4.5.3)
где ![]() , x,y;
, x,y; ![]() - координаты в поперечном сечении;
- координаты в поперечном сечении;
и тот же коэффициент в одномерном выражении:
![]() , (4.6.4)
, (4.6.4)
Физический смысл функции R(r) - степень зависимости значения в двух точках, разделенных расстоянием r. Значение функции нормировано, то есть, ее максимум равен единице. Максимум этот достигается в точке r=0 (по определению), а также на таких значениях r, на которых поле не изменяется. Когда значение R убывает до величины, близкой к нулю, это означает, что на таких расстояниях значения поля не коррелируют, то есть, успевают измениться достаточно сильно.
2. Сойфер В.А. Компьютерная оптика //Соросовский образовательный журнал, 1998
3. Франсон М. Голография.- М.: Мир, 1972, 248 с.
4. Горохов Ю.Г., Неплюев Л.Н. Голография в приборах и устройствах.- М.: Энергия,1974, 80 с.
5. Федоров Б.Ф., Цибулькин Л.М. Голография.- М.: Радио и связь, 1989, 140 с.
6. Кузнецова Т.И. О фазовой проблеме в оптике //УФН, 1988, т.154, в. 4, с. 677-690.
7. Воронцов М.А., Шмальгаузен В.И. Принципы адаптивной оптики.- М.: Наука, 1985, 336 с.
8. Воронцов М.А., Корябин А.В., Шмальгаузен В.И. Управляемые оптические системы. - М.: Наука, 1988, 270 с.
9. Гроссо Р., Еллин М. Мембранное зеркало как элемент адаптивной оптической системы //Сб. статей "Адаптивная оптика" под ред. Э.А. Витриченко - М.: Мир, 1980, с. 428-447.
10. Ярославский Л.П. Цифровая обработка полей в оптических системах. Цифровая оптика. //сб. "Новые физические принципы оптической обработки информации" под ред. С.А. Ахманова и М.А. Воронцова, - М.: Наука. Гл. ред. физ.-мат. лит., 1990, 400 с.
11. Мирошников М.М., Нестерук В.Ф. Развитие методологии иконики и ее структурной схемы //Труды Государственного оптического института им. С.И. Вавилова, 1982, т. 57, в. 185, с. 7- 13.
12. Сойфер В.А. Компьютерная обработка изображений. Часть 1. Математические модели //Соросовский образовательный журнал, 1996, №2, с.118-124.
13. Сойфер В.А. Компьютерная обработка изображений. Часть 2. Методы и алгоритмы //Соросовский образовательный журнал, 1996, №3, с.110-121.
| Дальше | К оглавлению |