2.4. Распространение когерентного излучения в среде со случайными неоднородностями [15-19]
Рассмотрим теперь распространение излучения в среде, показатель преломления которой изменяется случайным образом. При падении световой волны на такую случайную среду амплитуда и фаза волны претерпевают флуктуации, обусловленные флуктуациями показателя преломления среды.
2.4.1. Борновское приближение и приближение Рытова
В случайной среде относительная диэлектрическая проницаемость ![]() и показатель преломления n меняются от точки к точке и эти изменения нельзя предсказать; более того, даже если бы они и были известны, практически невозможно описать их значения во всех точках пространства. Поэтому среду необходимо описывать статистически и искать статистические закономерности поведения волны в такой среде. В соответствии с этим диэлектрическую проницаемость следует задавать как случайную функцию радиус-вектора r:
и показатель преломления n меняются от точки к точке и эти изменения нельзя предсказать; более того, даже если бы они и были известны, практически невозможно описать их значения во всех точках пространства. Поэтому среду необходимо описывать статистически и искать статистические закономерности поведения волны в такой среде. В соответствии с этим диэлектрическую проницаемость следует задавать как случайную функцию радиус-вектора r:
![]() (2.4.1)
(2.4.1)
Для неоднородного распределения показателя преломления приведенное волновое уравнение имеет вид
![]() . (2.4.2)
. (2.4.2)
Это уравнение непосредственно получается из уравнения (1.2.9) в предположении монохроматичности излучения. Показатель преломления n можно представить в виде суммы среднего значения <n> и флуктуаций n1. Как уже указывалось в комментарии к уравнению (1.2.9) (см. соотношения (1.2.21)-(1.2.23)), последним членом в (2.4.2) можно пренебречь, если длина волны ![]() много меньше расстояния, на котором заметным образом меняется показатель преломления. Для волн оптического диапазона это допущение чаще всего выполняется, что позволяет придать волновому уравнению более простую форму:
много меньше расстояния, на котором заметным образом меняется показатель преломления. Для волн оптического диапазона это допущение чаще всего выполняется, что позволяет придать волновому уравнению более простую форму:
![]() (2.4.3)
(2.4.3)
Используя среднее волновое число ![]() , где k0 - волновое число для вакуума, можно записать k1
, где k0 - волновое число для вакуума, можно записать k1
![]() (2.4.4)
(2.4.4)
Поставим задачу найти приближенное решение уравнения (2.4.4) для малых значений n1. Это можно сделать двумя cпособами. Один из них основан на разложении в ряд самого поля:
![]() (2.4.5)
(2.4.5)
Нулевой член ряда описывает падающую или невозмущенную волну, слагаемые первого порядка - однократно рассеянное поле, второго порядка - двукратно рассеянное и т.д. Модель однократного и многократного рассеяния иллюстрирует рис. 2.4.1. Другой способ использует разложение в ряд показателя экспоненты:
![]() (2.4.6)
(2.4.6)
Разложение (2.4.5) представляет собой так называемое борновское приближение, а разложение (2.4.6) называется разложением Рытова. Рассмотрим первые приближения этих разложений.
Начнем с борновского приближения. Запишем уравнение (2.4.4) в виде
![]() (2.4.7)
(2.4.7)
где
![]()
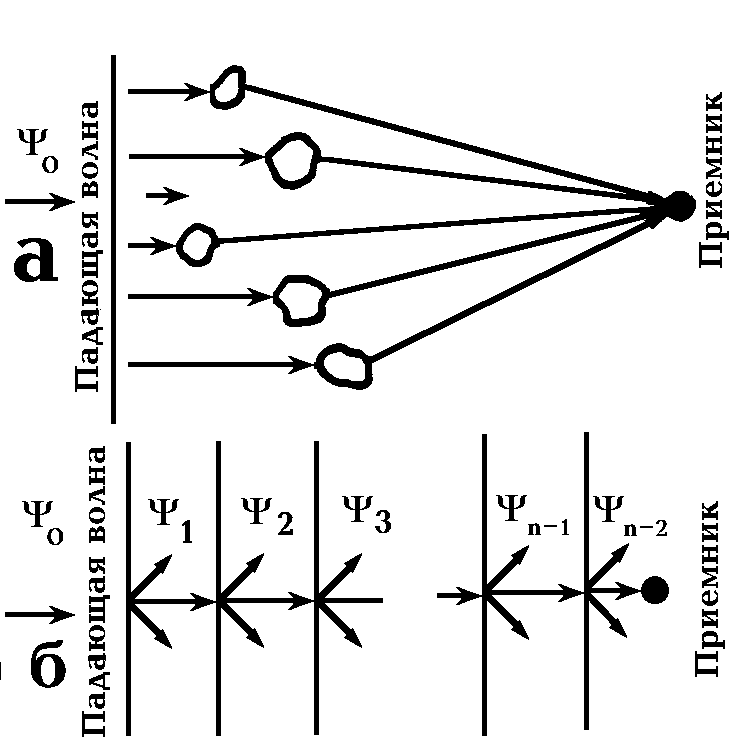
Рис. 2.4.1 Модели однократного (а) и многократного (б) рассеяния
Это уравнение можно свести к следующему интегральному уравнению для y :
(2.4.8)
где ![]() - поле в отсутствие флуктуаций
- поле в отсутствие флуктуаций ![]() , а
, а
![]() (2.4.9)
(2.4.9)
функция точечного источника.
Из уравнения (2.4.8) видно, что поле рассеянной волны, наблюдаемое в точке r, обусловлено сферической волной ![]() , исходящей из точки r'. Амплитуда сферической волны пропорциональна произведению амплитуды поля распространяющегося в среде излучения на флуктуирующую часть показателя преломления n1(r'), а фаза определяется общим числом длин волн, укладывающихся на пути от источника до рассеивателя и далее до приемника.
, исходящей из точки r'. Амплитуда сферической волны пропорциональна произведению амплитуды поля распространяющегося в среде излучения на флуктуирующую часть показателя преломления n1(r'), а фаза определяется общим числом длин волн, укладывающихся на пути от источника до рассеивателя и далее до приемника.
Если подставить в интеграл y 0, то получится первая итерация y 1 борновского приближения. Продолжая последовательность итераций, можно получить выражение для y в виде ряда.
Рассмотрим теперь приближение Рытова. Поле y (r) можно записать в виде
![]() (2.4.10)
(2.4.10)
и искать решение для ![]() в виде ряда. Этот подход, известный под названием метода Рытова, широко используется в задачах распространения волн в пределах прямой видимости. Имеется ряд теоретических и экспериментальных подтверждений того, что в задачах распространения в пределах прямой видимости первое приближение Рытова является более точным, чем борновское приближение.
в виде ряда. Этот подход, известный под названием метода Рытова, широко используется в задачах распространения волн в пределах прямой видимости. Имеется ряд теоретических и экспериментальных подтверждений того, что в задачах распространения в пределах прямой видимости первое приближение Рытова является более точным, чем борновское приближение.
Используя уравнение (2.4.7) и представление (2.4.10), а также полагая, что
![]() (2.4.11)
(2.4.11)
можно получить следующее интегральное уравнение для ![]() :
:
![]() (2.4.12)
(2.4.12)
Уравнения типа (2.4.12) обычно решаются методом итераций с представлением решения в виде ряда. Упростим уравнение (2.4.12), полагая, что
![]() , (2.4.12a)
, (2.4.12a)
или
![]() . (2.4.12b)
. (2.4.12b)
Это предположение означает, что изменения ![]() на расстояниях порядка длины волны должны быть малыми по сравнению с d
n и происходить достаточно плавно. Тем самым и метод, основанный на использовании допущения (2.4.12a,b), получил название метода плавных возмущений (МПВ). Таким образом, пренебрегая под знаком интеграла (2.4.12) произведением
на расстояниях порядка длины волны должны быть малыми по сравнению с d
n и происходить достаточно плавно. Тем самым и метод, основанный на использовании допущения (2.4.12a,b), получил название метода плавных возмущений (МПВ). Таким образом, пренебрегая под знаком интеграла (2.4.12) произведением ![]() , находим первую итерацию
, находим первую итерацию
![]() (2.4.13)
(2.4.13)
которая представляет собой первое приближение Рытова и широко используется в теории слабых флуктуаций.
Итак, приближение Рытова представимо в виде:
![]() (2.4.14)
(2.4.14)
Представление ![]() в виде итерационного ряда может быть найдено из следующего уравнения, получающегося из (2.4.12) и (2.4.13):
в виде итерационного ряда может быть найдено из следующего уравнения, получающегося из (2.4.12) и (2.4.13):
![]() (2.4.15)
(2.4.15)
Подставляя ![]() под знаком интеграла, приходим к следующей итерации. Продолжая эту процедуру, можно найти выражение для
под знаком интеграла, приходим к следующей итерации. Продолжая эту процедуру, можно найти выражение для ![]() в виде ряда.
в виде ряда.
2.4.2. Флуктуации уровня и фазы
Рассмотрим первое приближение Рытова для слабо неоднородной среды. В этом случае удобно использовать приближенное равенство
![]() (2.4.16)
(2.4.16)
и записать
![]() (2.4.17)
(2.4.17)
![]() (2.4.18)
(2.4.18)
где
![]() (2.4.19)
(2.4.19)
Соотношение (2.4.18) устанавливает связь поля ![]() с флуктуациями показателя преломления
с флуктуациями показателя преломления ![]() .
.
Найдем теперь выражения для амплитуды A и фазы S поля y (r). Полагая
![]() ,
, ![]() (2.4.20)
(2.4.20)
получаем![]()
![]()
![]() . (2.4.21)
. (2.4.21)
Вещественная часть ![]() , обозначенная через
, обозначенная через
| Дальше | К оглавлению |