Использованное в предыдущих разделах понятие моды является не совсем строгим, так как требование сохранения в процессе распространения формы амплитудно-фазового профиля не сочеталось с требованием неизменности поперечных размеров светового поля. Тем не менее, в некоторых оптических системах и средах возможно распространение волновых пучков, удовлетворяющих одновременно двум сформулированным выше требованиям. Такие волновые пучки представляют собой истинные моды с точки зрения их корректного определения. Если световое поле в оптической системе представимо в виде такого рода мод, то говорят о возможности волноводного распространения излучения.

Анализ волноводного распространения излучения начнем с пучков в квадратичных средах. Квадратичной средой называется среда, показатель преломления которой меняется в поперечном направлении по квадратичному закону

(2.3.1)

Квадратичная среда обладает волноводными свойствами, распространение в ней световых волн во многом сходно с распространением света в линзовом волноводе, состоящем из последовательности собирающих линз. Модель квадратичной среды широко используется как при анализе распространения излучения через лазерные активные элементы, так и при изучении распространения света в некоторых типах оптических волокон. Однако эта модель имеет один серьезный недостаток. Как видно из (2.3.1) при больших значениях поперечных координат x и y показатель преломления становится меньше единицы и даже достигает отрицательных значений. Модель квадратичной среды будет, тем самым, иметь смысл для пучков, основная часть энергии которых концентрируется вблизи оси и не выходит за пределы области, где n>1.

Для большинства реальных оптических сред, свойства которых близки к квадратичной модели (2.3.1), относительные изменения показателя преломления по длине световой волны малы и определяемый выражением (1.2.21) параметр R<<1. Поэтому для определения мод квадратичной среды можно воспользоваться приведенным уравнением в форме

(2.3.2)

где k0 выражается через длину волны l в свободном пространстве , а

(2.3.3)

Если считать исходным показатель преломления (2.3.1), то (2.3.3) является приближенным соотношением. Как и для свободного пространства, уравнение (2.3.2) решается с помощью пробной функции

(2.3.4)

Опуская промежуточные выкладки, запишем сразу общий вид получающегося решения

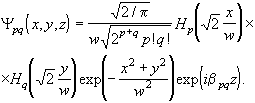(2.3.5)

Мы видим, что модовыми решениями для волн в квадратичной среде опять-таки являются функции Эрмита-Гаусса. Радиус пучка основной моды оказывается равным

(2.3.6)

и не зависит от продольной координаты z. Постоянная распространения b pq будет определяться выражением

(2.3.7)

Заметим, что в отличие от модового решения для свободного пространства, решение (2.3.5) является точным решением cкалярного волнового уравнения. При этом моды среды, квадратичной по показателю преломления, всегда имеют плоский волновой фронт.

Рассмотренные моды являются модами квадратичной среды, которая не вносит ни затухания ни усиления. Такое предположение, естественно, является идеализацией. Чтобы учесть затухание или усиление, в дополнение к вышеприведенному анализу рассмотрим квадратичные среды с комплексной диэлектрической проницаемостью. Если по квадратичному закону изменяется лишь действительная часть показателя преломления, мы имеем ситуацию, когда направленность волн определяется фокусирующими свойствами среды, обладающей на оси максимальным значением действительного показателя преломления. Применительно к средам с комплексной диэлектрической проницаемостью можно показать, что в тех случаях, когда усиление уменьшается с увеличением расстояния от оси, а потери, наоборот, возрастают при удалении от оси, в среде могут распространяться направленные моды, даже если действительная часть показателя преломления однородна или увеличивается при удалении от оси.

Рассматривая диэлектрическую среду с комплексным показателем преломления, нет необходимости вновь решать волновое уравнение. Выше приведенное решение справедливо также и для комплексных значений n₀ и n₁. Полиномы Эрмита являются аналитическими функциями даже при комплексных значениях своего аргумента.

Допустим, что n₀ имеет комплексное значение

(2.3.8)

Положительные и отрицательные значения n_0i относятся к средам соответственно с потерями и усилением. В реальных физических средах всегда

(2.3.9)

так что можно записать

(2.3.10)

Введем еще одну комплексную величину

(2.3.11)

Величина (2.3.6) является теперь комплексной. Ее смысл как квадрата радиуса пучка сохраняется для реальной части. Помня, что w является комплексной величиной, воспользуемся выражением (2.3.5) для описания моды в квадратичной среде с комплексной диэлектрической проницаемостью

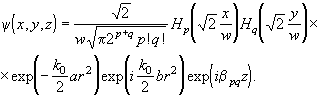(2.3.12)

Чтобы поле направленной моды спадало с ростом величины , необходимо потребовать, чтобы выполнялось условие

(2.3.13)

Из выражения (2.3.12), описывающего структуру моды, видно, что волновые фронты в среде с комплексным показателем преломления не являются плоскими. Их форма является более сложной, поскольку они определяются не только экспоненциальными функциями, но и комплексными значениями полиномов Эрмита. Для основной моды волновой фронт при положительных значениях b является вогнутым, если смотреть в положительном направлении оси z. Для того, чтобы установить связь величины b с показателем преломления, воспользуемся формулами (2.3.8) и (2.3.11) и запишем вещественную и мнимую части выражения (2.3.1)

(2.3.14)

(2.3.15)

Выражения (2.3.14) и (2.3.15) записаны в пренебрежении малыми членами с произведением на и ab.

Так как a - величина положительная, то положительное значение b означает, что с увеличением r в среде растут потери. Предположим, что величина отрицательная. Тогда среда уcиливает на оси при r=0. Для положительного b усиление падает при удалении от оси. Поскольку при этом у лучей, перпендикулярных волновому фронту, появляется радиальная составляющая, направленная к периферии пучка, энергия, возникающая вблизи оси, будет уходить от нее и поглощаться.

Если поведение мнимой части показателя преломления полностью зависит от знака b, так как всегда a>0, то поведение действительной части показателя преломления зависит от того, больше a2, чем b2 или меньше. Re n уменьшается с ростом r, если , и увеличивается, если . Направленная волноводная мода может существовать как в первом, так и во втором случаях.

Заметим, что теоретически нельзя исключать возможность существования моды в среде с b<0, однако, анализ решения волнового уравнения (2.3.12) на устойчивость показывает, что при b<0 мода среды является неустойчивой, даже малые возмущения в системе могут привести к разрушению модовой структуры.

В заключение рассмотрим процесс затухания или усиления мод для случая комплексного показателя преломления. Постоянную распространения (2.3.7) можно разложить на действительную и мнимую части:

, (2.3.16)

(2.3.17)

Затухание или усиление определяется мнимой частью b _pq. Моды усиливаются, если I_{mb pq}<0, и испытывают поглощение, если I_{mb pq}>0. Вопрос, усиливается или поглощается мода, зависит от трех факторов: знака , знака b и величины p+q+1.

Для передачи когерентного излучения в волноводном режиме между элементами различного рода оптических устройств или систем широко используются оптические волокна. Оптическое волокно рис. 2.3.1 представляет собой внутреннюю диэлектрическую среду (стекло, кварц и т.п.), в которой содержится основная часть световой энергии, передаваемой по волокну в волноводном режиме. Эта внутренняя среда называется сердцевиной. Сердцевина может быть окружена слоем с более низким показателем преломления, называемым оболочкой. Для защиты от внешних воздействий сердцевину с оболочкой часто покрывают защитным слоем пластмассы. Обычно оптические волокна имеют круглую форму. Существует два основных типа круглых волокон. К первому типу относится волокно со скачком показателя преломления (рис. 2.3.1, a). В нем показатель преломления сердцевины характеризуется постоянным значением, и волноводное распространение излучения обеспечивается эффектом полного внутреннего отражения между сердцевиной и оболочкой. Второй тип волокон имеет сердцевину, показатель преломления которой изменяется в зависимости от расстояния r от оптической оси по параболическому закону

(2.3.18)

(рис. 2.3.1, б) Волокна этого типа обычно называют волокнами с градиентом показателя преломления или градиентными волокнами.

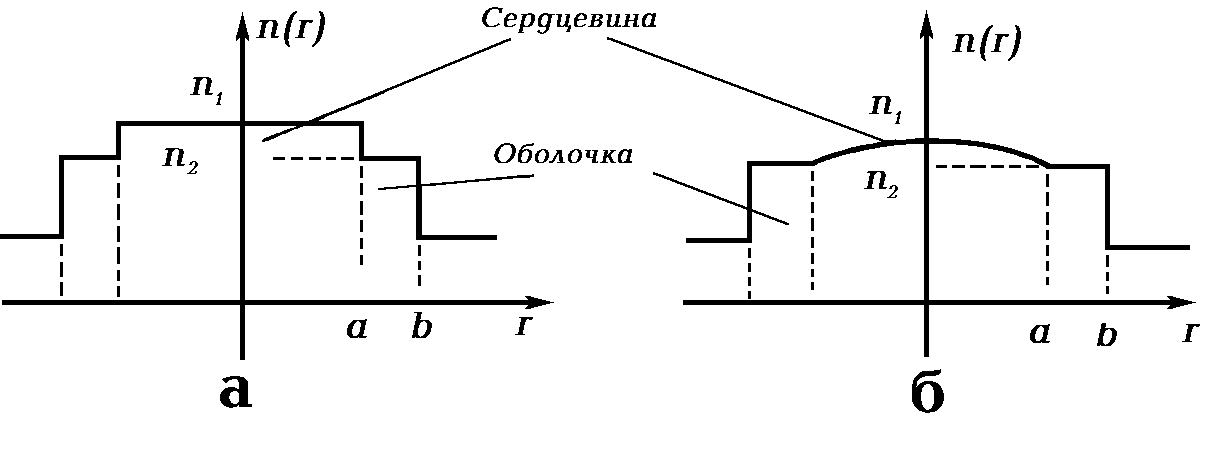
Каждому типу волокон может быть поставлена в соответствие система волноводных мод. Отдельные моды или их суперпозиции определяют структуру излучения, распространяющегося по волокну. На градиентные волокна полностью переносится теория волноводных мод, изложенная в разделе 2.3.1 для сред, квадратичных по показателю преломления.

Что касается характеристик мод волокон со скачком показателя преломления, то их определяют на основе поиска решений приведенного волнового уравнения с постоянным коэффициентом для сердцевины и оболочки с последующей процедурой их "сшивания". Среди мод такого волокна выделим в качестве наиболее часто встречающихся на практике поперечные поляризованные моды типа EH, структура которых определяется выражениями:

при r<a

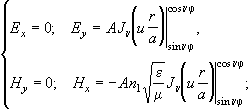(2.3.19)

при r>a

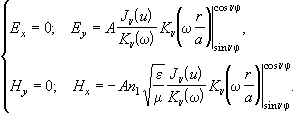(2.3.20)

Здесь A - постоянная величина; E_x, E_y и H _x, H_y - поперечные составляющие электрического и магнитного полей; Jn - функции Бесселя; Kn - модифицированные функции Бесселя;

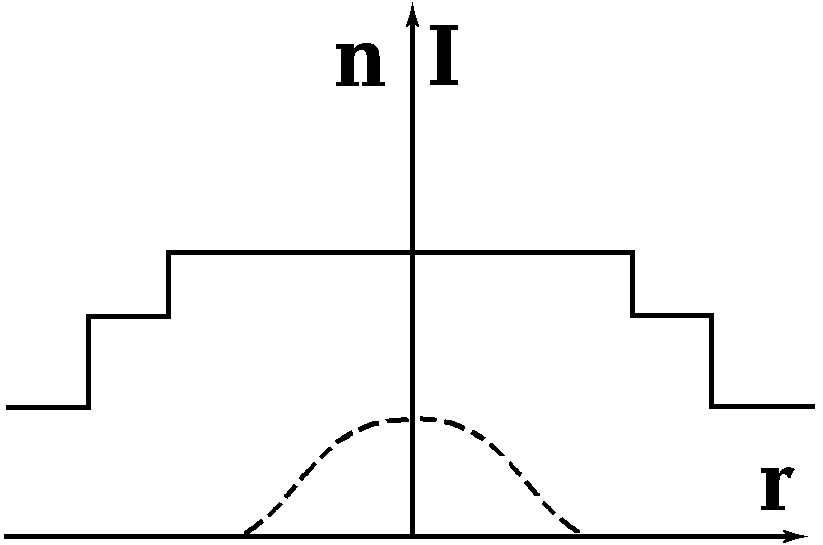
Низшая из приведенных мод хорошо описывается гауссовой кривой. Это, в частности, видно из рис. 2.3.2, где приведен профиль интенсивности для низшей моды. Подобное распределение интенсивности обеспечивает хорошее ее согласование посредством линзы с основной модой лазера, излучение которого направляется в волокно.

В лазерной физике и технике широко используются газовые и жидкостные лазеры, в которых активная среда находится внутри полого диэлектрического волновода. Такие лазеры способны генерировать одночастотное излучение, перестраиваемое в широком спектральном интервале. Это делает их весьма ценным инструментом при решении многих задач когерентной оптики. Полым диэлектрическим волноводам, в роли которых часто выступают обычные стеклянные, кварцевые или керамические трубки, можно поставить в соответствие целую систему волноводных мод. Не останавливаясь подробно на выводе выражений для мод полого волновода, исходя из уравнения Гельмгольца, ограничимся краткой характеристикой их свойств.

Можно выделить три основных типа мод:

1) поперечные электрические моды ТЕ_0m, в которых электрическое поле направлено по касательной к поверхности волновода;

2) поперечные магнитные моды ТЕ_0m, в которых электрическое поле перпендикулярно к волноводной поверхности;

3) смешанные моды ЕН_nm, в которых электрическое поле имеет радиальную и тангенциальную составляющие.

В практическом отношении наиболее интересны смешанные гибридные ЕН_nm моды (n¹ 0; m³ 1), так как именно эти моды возбуждаются в большинстве лазерных волноводов. Если показатель преломления стенок волновода n₀<2.02, то наименьшими потерями обладает волноводная мода ЕН₁₁, у которой распределение поля излучения описывается бесселевой функцией нулевого порядка (r - радиальная компонента, а - радиус круглого волновода). Эта мода линейно поляризована и наилучшим образом связана с основной модой свободного пространства ТЕМ₀₀.

Тангенциальная и радиальная составляющие электрического поля гибридных мод более высокого порядка даются выражениями

;

(2.3.21)

,

где - m-ый корень уравнения , q - азимутальная координата, - функция Бесселя n-го порядка. Считается, что все рассматриваемые моды удовлетворяют соотношению

, (2.3.22)

где l - длина волны излучения. Помимо моды ЕН₁₁ линейно поляризованными будут моды ЕН_1m, а также суперпозиции мод и .

Константа распространения гибридных мод круглого волновода имеет вид

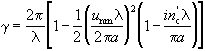. (2.3.23)

Набег фазы и коэффициент затухания даются действительной и мнимой частями последнего выражения:

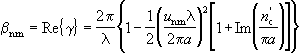; (2.3.24)

, (2.3.25)

где

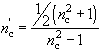. (2.3.26)

Теоретические оценки показывают, что моды полых диэлектрических волноводов имеют весьма малые потери. Так, мода ЕН11 с длиной l =1 мкм распространяется в стеклянном волноводе с показателем преломления =1.5 и внутренним радиусом a =1 мм испытывая потери, равные всего лишь 1.85 дБ/км. Однако потери в волноводе критичны по отношению к изгибам. Так, потери для моды ЕН₁₁ удваиваются, если радиус кривизны волновода составит 10 км.

Если отношение l /а пренебрежимо мало, то волновые фронты волноводных мод можно с большой степенью точности считать плоскими. В силу этого обстоятельства эффективная обратная связь в волноводном резонаторе может быть осуществлена с помощью плоских зеркал с высоким коэффициентом отражения, помещенных непосредственно на торцах волновода (одно из зеркал - выходное - обычно выполняется полупрозрачным). В такой системе при отражении от зеркала резонатора не происходит изменение модового состава излучения. Из условия резонанса, согласно которому вдоль волновода должно укладываться целое число полуволн, можно получить следующее выражение для собственных частот резонатора:

, (2.3.27)

где q=0, 1, 2...., L - длина резонатора, с и l ₀ - соответственно скорость и длина волны света в свободном пространстве, .

Распределение поля в сечении генерируемого таким лазером светового пучка будет определяться дифракцией волноводной моды на торце волновода. Профиль распределения интенсивности центрального дифракционного пятна очень близок к гауссовому, в результате чего 98% энергии волноводной моды переходит в моду свободного пространства ТЕМ₀₀. При этом минимальный радиус пучка гауссовой моды w₀ связан с радиусом круглого волновода а соотношением

(2.3.28)

(горловина ТЕМ₀₀ моды лежит в плоскости торца волновода).