В лазерных устройствах широко используются оптические резонаторы, состоящие чаще всего из двух плоскопараллельных или сферических зеркал. Оптические резонаторы обеспечивают необходимую для лазерной генерации положительную обратную связь и позволяют повысить плотность мощности светового поля до уровня, при котором происходит эффективный съем энергии с активной лазерной среды. Геометрия резонатора во многом определяет структуру лазерных пучков. В данном параграфе будут рассмотрены пространственные спектральные характеристики собственных типов колебаний (мод) оптических резонаторов, наиболее часто используемых в лазерной технике.

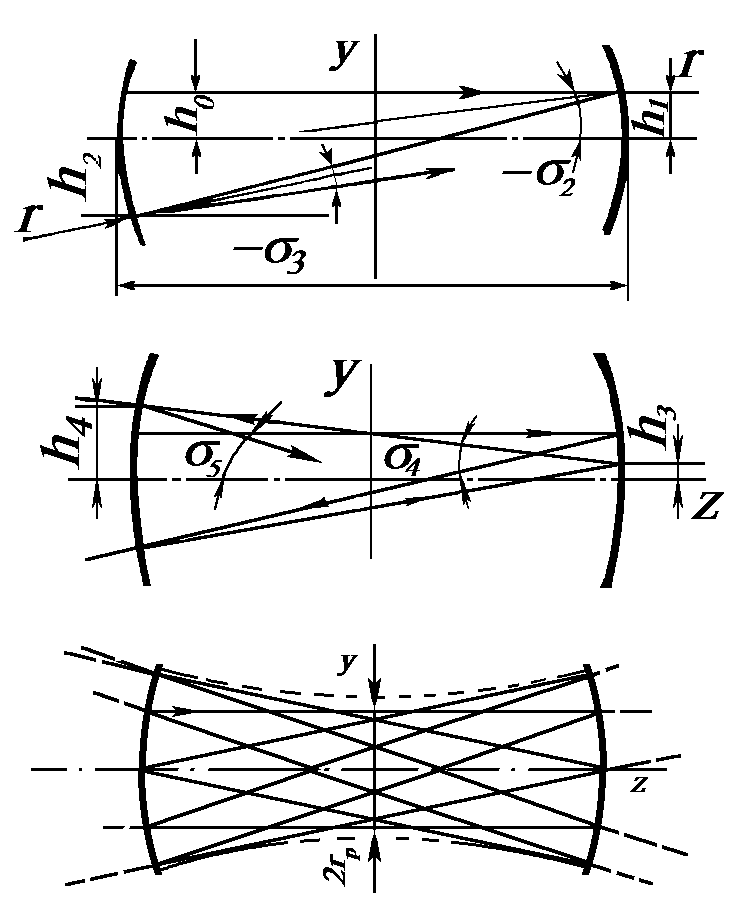
Как известно, традиционная схема лазера включает в себя двухзеркальный резонатор и располагающуюся в его внутренней полости активную среду. Рассмотрим симметричный лазерный резонатор со сферическими зеркалами (рис. 2.2.1). Луч, идущий вблизи оси резонатора, усиливается в активной среде и испытывает периодические отражения от зеркал. При каждом отражении луч частично проходит через зеркало и покидает резонатор. Отраженный луч усиливается и при следующем отражении снова частично выходит из резонатора и так далее. Таким образом, пучок света, выходящий из лазерного резонатора, можно представить в виде совокупности лучей (лучевого пакета), являющихся продолжениями первоначального луча после каждого его отражения от зеркал. Траекторию меридионального луча несложно определить, используя матричный метод, описанный в разделе 2.1.5. При использовании приведенных в указанном разделе соотношений надо воспользоваться тем, что с точки зрения воздействия на луч зеркало эквивалентно линзе с фокусным расстоянием f=R/2. Оценивая изменение координат луча путем последовательного применения матриц зеркала и свободного промежутка между зеркалами, можно показать, что поперечная координата hk луча при k-м отражении, начиная с k=0, определяется соотношением:

(2.2.1)

где h0 и s 0 - поперечные линейная и угловая координаты луча при первом отражении, соsw =g (0<g<1), где g - так называемый g-фактор резонатора, выражаемый через его длину d и радиус кривизны зеркала R посредством соотношения. Неравенство определяет условие устойчивости симметричного резонатора. Если оно нарушено, то луч после определенного числа отражений обязательно выйдет за границы апертуры зеркал. Такие резонаторы называются неустойчивыми.

В общем случае, когда w не кратно целому числу p , точки, в которых происходит отражение луча на зеркалах резонатора, не повторяются. Луч при этом, несмотря на дискретный характер отражения, стремится полностью зачертить некоторую область внутри резонатора. Граница этой области является огибающей лучевого пакета (каустикой), т.е. описывает форму лазерного пучка в геометрооптической трактовке.

Приведенный лучевой анализ структуры поля в устойчивом симметричном резонаторе может быть распространен и на случай несимметричного резонатора с разными радиусами кривизны зеркал. Опуская получающиеся при этом соотношения, отметим лишь, что условие устойчивости резонатора с радиусами кривизны зеркал R1 и R2 имеет вид:

0<g1g2<1, (2.2.2)

где g1=1-d/R1 и g2=1-d/R2 - g-факторы несимметричного резонатора. Лучевые модели описания внутрирезонаторных полей получили широкое распространение прежде всего в силу их простоты и наглядности. Однако не всегда при этом дается отчет в том, что указанные модели не удовлетворяют условиям выполнимости геометрооптического приближения. Некорректность лучевых моделей особенно отчетливо проявляется применительно к устойчивым резонаторам. В устойчивом резонаторе лазерный пучок формируется в прикаустической зоне и значительные изменения амплитуды поля происходят на масштабе, меньшем первой зоны Френеля. Отступление от классической трактовки геометрической оптики приводит к тому, что распространяющиеся в резонаторе лучи оказываются неперпендикулярными волновому фронту. В этой связи в когерентной оптике сложилось направление, рассматривающее внутрирезонаторные лучевые модели в виде неких модификаций геометрической оптики. Разработанная в рамках данного направления теория [8,9] позволяет по определенным правилам восстанавливать амплитудно-фазовый профиль пучка внутри резонатора на основе структуры лучевых пакетов.

В волновой трактовке свойства устойчивых резонаторов во многих случаях целесообразно рассматривать в приближении бесконечной апертуры зеркал. Такое приближение является оправданным, когда поле лазерного излучения концентрируется вблизи оси резонатора и его величина у краев зеркал пренебрежимо мала. Последнее обстоятельство освобождает от рассмотрения эффектов дифракции на внешней апертуре зеркал и позволяет свести моды устойчивых резонаторов к изученным уже в разделе 2.1 модам свободного пространства. В этом разделе было показано, что эрмито-гауссовые или лагерро-гауссовые моды свободного пространства имеют область наибольшего сужения (горловину) и расширяются от этой области в обоих направлениях. Типичный гауссов пучок показан на рис. 2.2.2,а. Сплошные линии характеризуют ширину пучка, а пунктирные линии, перпендикулярные оси, показывают фазовые фронты в различных точках вдоль пучка. Такой же пучок может существовать и внутри устойчивого резонатора, если зеркала поместить в тех местах, где радиусы кривизны фазового фронта пучка совпадают с радиусами кривизны (рис. 2.2.2, б).

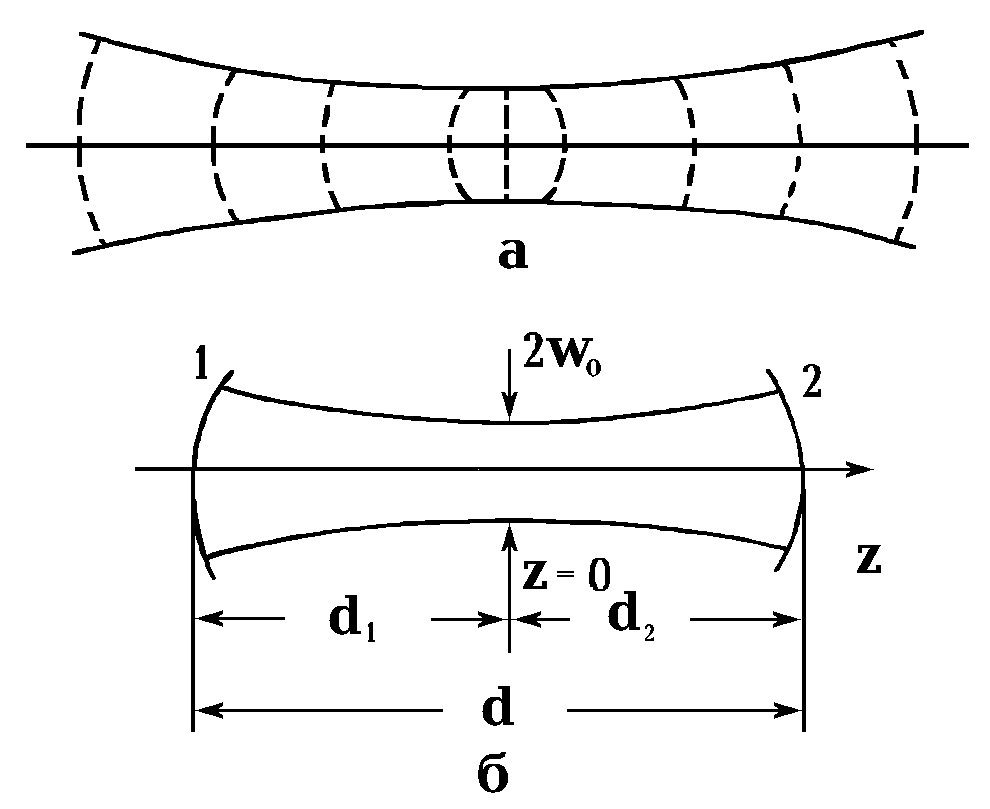
При каждом отражении от зеркал пучок будет переходить сам в себя, что и обеспечит формирование моды резонатора. Поскольку все принадлежащие к одному семейству моды Эрмита-Гаусса и Лагерра-Гаусса характеризуются одними и теми же значениями радиуса кривизны волнового фронта, можно утверждать, что устойчивому сферическому резонатору можно поставить в соответствие целый набор собственных мод ТЕМmn, различающихся поперечными индексами m и n. Их структура определяется выражениями (2.1.12, 2.1.13, 2.1.22, 2.1.26). Входящие в эти выражения минимальный радиус гауссова пучка и длина волны l могут быть найдены из условия резонанса, обеспечивающего интерференцию на усиление лучей, отраженных от зеркал резонатора. Условие резонанса будет выполняться, если фазовый сдвиг внутрирезонаторного пучка за двойной проход по резонатору будет равен целому числу, умноженному на 2p . Тем самым, при резонансе должно выполняться равенство

2D F = 2 N p , (2.2.3)

где D F - сдвиг фазы при прохождении волны от одного зеркала к другому, N - целое число. На оси резонатора (r=0) согласно (2.1.23)

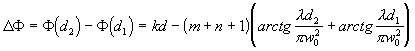. (2.2.4)

Считается, что зеркала расположены на расстояниях d1 и d2 от области сужения пучка и d=d1+ d2 (см. рис. 2.2.2,б). С учетом (2.2.4) условие резонанса (2.2.3) принимает вид

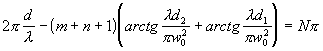. (2.2.5)

Длина волны l в приведенных соотношениях является не длиной волны моды гауссова пучка, а длиной волны, которую имела бы соответствующая плоская волна, если бы она распространялась в той же среде и с той же частотой, что и мода гауссова пучка. Длина волны гауссова пучка могла быть определена как расстояние вдоль оси, соответствующее фазовому сдвигу 2p . Ее величина, однако, не является постоянной и зависит, хотя и незначительно, от положения вдоль оси моды Эрмито-Гаусса.

Условие резонанса (2.2.5) можно выразить непосредственно через параметры резонатора. Выразим сначала расстояния d1 и d2, радиусы пучков w1 и w2 на зеркалах 1 и 2, минимальный радиус пучка w0 через радиусы кривизн зеркал R1 и R2 и расстояние d между ними. Используя зависимость (2.1.13), можно записать

, (2.2.6)

. (2.2.7)

Освобождаясь от величины w0 в этих уравнениях, получаем

. (2.2.8)

Присовокупив к (2.2.8) равенство

, (2.2.9)

можно определить неизвестные параметры d1 и d2

, (2.2.10)

. (2.2.11)

Подстановкой (2.2.10) и (2.2.11) в (2.2.6) или (2.2.7) находим последний неизвестный параметр - минимальный радиус пучка w0

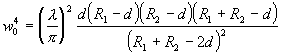. (2.2.12)

Используя выражения (2.2.10), (2.2.11) и (2.1.12), легко найти величину радиусов пучков на зеркалах резонатора

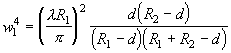, (2.2.13)

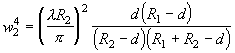. (2.2.14)

Вышеприведенные выражения позволяют условие резонанса (2.2.5) записать в форме, включающей в явном виде параметры резонатора. Воспользуемся известной тригонометрической формулой

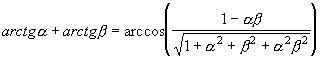, (2.2.15)

где

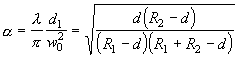, (2.2.16)

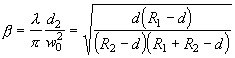. (2.2.17)

Путем алгебраических упрощений выражение (2.2.15) можно привести к виду

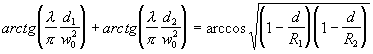. (2.2.18)

С учетом (2.2.18) условие резонанса (2.2.5) примет вид

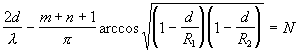. (2.2.19)

Выражение (2.2.19) позволяет определить резонансную частоту (собственную частоту резонатора)

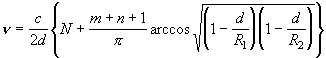. (2.2.20)

Заметим, что последнее выражение сочетается с условием устойчивости (2.2.1), поскольку член под знаком корня может быть только действительной величиной, а модуль корня должен быть меньше единицы. Число N определяет число полуволн, укладывающихся вдоль оси резонатора. Поэтому число N часто называют порядком продольных мод резонатора или продольным индексом. Индексы же m и n называют индексами резонаторных мод, поскольку они определяют число поперечных вариаций поля эрмито-гауссовых мод. При m=n=0 имеет место чисто гауссова мода. Таким образом, чтобы охарактеризовать пространственную структуру собственной моды резонатора помимо параметров d1, d2, w0, w1,2 нужно обязательно задать один продольный N и два поперечных индекса m и n.

Если зафиксировать поперечные индексы m и n, то из (2.2.20) легко установить, что частотный интервал между соседними "продольными² модами (продольный индекс которых отличается на единицу) равен с/2d.

Если структуру поля в резонаторе описывать с помощью лагерро-гауссовых мод, то их параметры по-прежнему будут определяться выражениями (2.2.10) - (2.2.14). Резонансные же частоты будут определяться выражением

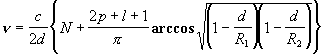. (2.2.21)

Для конфокального резонатора (d=R1=R2=b) параметры собственной моды принимают значения

, , , (2.2.22)

собственная же частота моды будет определяться выражением

. (2.2.23)

Параметр b называют конфокальным параметром. Самая важная особенность конфокального резонатора состоит в том, что в нем достигается высокая степень вырождения собственных мод: моды, имеющие различный набор индексов m, n, N могут иметь совпадающие частоты. Действительно, из (2.2.23) видно, что значение собственной частоты резонатора n не изменится, если сумму поперечных индексов m+n увеличить на целое число 2К (К=1, 2, 3...), а индекс N уменьшить на К. Как следует из (2.2.23), минимальный частотный интервал между четными и нечетными модами резонатора, сумма поперечных индексов которых m+n является соответственно четной и нечетной, равен с/4d.

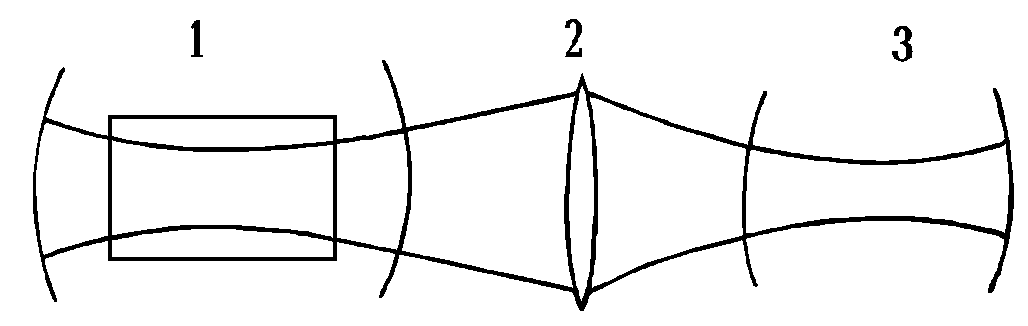
Установив зависимость между параметрами генерируемого в лазере светового пучка от параметров лазерного резонатора, рассмотрим важную в практическом отношении задачу согласования моды одного резонатора с модой другого посредством тонкой линзы. Такая задача часто возникает, когда выходной лазерный пучок подается в пассивный сферический резонатор, выполняющий роль интерферометра, или в регенеративный оптический квантовый усилитель (невозбужденный лазер). Если не обеспечить согласование параметров лазерного пучка с параметрами собственной моды внешней системы, то возникает преобразование моды.

Рассмотрим согласование резонаторов лазера и интерферометра, когда известны положения горловин их собственных мод и минимальные радиусы пучков (рис. 2.2.3 ). Предположим, что минимальный радиус пучка лазера равен w10, а расстояние от его горловины до линзы есть z1. Соответствующие величины для собственного пучка интерферометра пусть будут равны w20 и z2. В горловинах комплексные параметры пучков будут чисто мнимые и равны

, . (2.2.24)

На основании уравнений (2.1.11) и (2.1.28) получаем следующее соотношение

. (2.2.25)

где f - фокусное расстояние линзы. Так как параметры пучка q1 и q2 являются чисто мнимыми, уравнение (2.2.25) можно разделить на вещественную и мнимую части

, (2.2.26)

. (2.2.27)

Найдем теперь, например, величину z2 путем исключения z1. При этом получим следующее квадратное уравнение:

. (2.2.28)

Решение уравнения (2.2.28) будет действительным, если

, где . (2.2.29)

Уравнения (2.2.26) и (2.2.27) могут быть представлены в виде

, (2.2.29а)

. (2.2.30)

Обращает на себя внимание сходство уравнения (2.2.30) с известной в геометрической оптике формулой линзы Ньютона. Отличие состоит лишь в наличии члена f02.

С уменьшением размеров зеркал резонатора следует считаться с проявлениями эффектов дифракции. Последние приведут к потерям энергии на внешней апертуре зеркал. В этом случае мода резонатора представляет собой определенную конфигурацию медленно затухающего поля с относительным распределением амплитуды, не изменяющейся во времени. В случае лазерной генерации потери энергии компенсируются за счет активной среды, что обеспечивает существование стационарного поля.

Для расчета поля резонаторов с конечной апертурой зеркал может быть привлечен принцип Гюйгенса в формулировке Френеля-Кирхгофа (1.2.34). Если распределение поля на зеркале 1 (см. рис. 2.2.2) задать функцией u1, то поле на зеркале 2 будет определяться дифракционным интегралом

, cosg =1, (2.2.31)

где А - площадь каждого из зеркал. Отразившись от зеркала 2, световая волна начнет распространяться в обратном направлении. Таким образом, она будет распространяться в резонаторе вперед и назад, попеременно отражаясь от его зеркал. После q проходов связь поля у одного зеркала с полем у другого зеркала будет опять же определяться выражением (2.2.31), где поле u1 следует заменить на uq, а u2 на uq+1.

После большого числа проходов распределение поля у зеркал будет подвергаться незначительным изменениям от отражения к отражению и со временем станет стационарным. На этой стадии поля около зеркал становятся одинаковыми с точностью до комплексной постоянной, что позволяет записать соотношение

, (2.2.32)

где v - функция распределения, не изменяющаяся от отражения к отражению, и g - комплексная постоянная, которая не зависит от координат. Подставляя (2.2.32) в (2.2.31), получаем интегральное уравнение

, (2.2.33)

где ядро

.

Функцию распределения поля v можно рассматривать как моду резонатора. Дифракционные потери моды определяются выражением

, (2.2.34)

где q - энергия, теряемая при одном прохождении из-за дифракции на зеркалах. Фазовые набеги моды связаны с величиной g соотношением

b =угол g , (2.2.35)

где b - фазовый сдвиг, претерпеваемый волной при распространении от одного зеркала к другому, в дополнение к фазовому сдвигу плоской волны, определяемому как 2p d/l . Если суммарные потери в резонаторе малы, добротность резонатора может быть представлена в виде

, (2.2.36)

где q t - суммарные потери, включая дифракционные потери, потери на пропускание, поглощение и рассеяние. Резонансная частота будет определяться соотношением

. (2.2.37)

Интегральное уравнение (2.2.33) можно решить численным методом последовательных приближений, который во многом аналогичен описанному выше физическому процессу возбуждения начального распределения поля световой волны в резонаторе и распространению его взад и вперед между зеркалами. Сначала на зеркале 1 задается произвольное распределение поля, а затем с помощью преобразования (2.2.31) последовательно находятся поля на зеркалах после каждого нового прохода. Расчет показывает, что после 300 отражений световой волны, флуктуации, наблюдающиеся от прохода к проходу, составляют менее 0.03% от средней величины, тем самым распределение амплитуды и фазы после 300 проходов можно поставить в соответствие определенной моде резонатора.

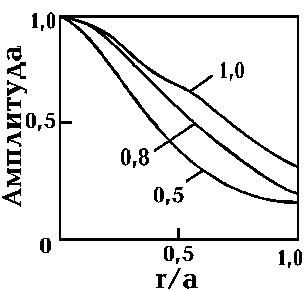
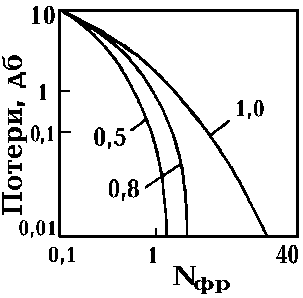
На рис. 2.2.4 приведено полученное в результате расчета относительное распределение поля моды ТЕМ00 симметричного резонатора с круглыми зеркалами радиуса а. На рис. 2.2.5 для такого же резонатора приведена зависимость дифракционных потерь моды ТЕМ₀₀ от числа Френеля Nфр=a2/l d (число Nфр равно числу зон Френеля, перекрываемых зеркалом резонатора при помещении точки наблюдения в центр противоположного зеркала). Цифрами у кривых обозначена величина g-фактора резонатора. Из рис. 2.2.4 и 2.2.5 видно, что конечный

размер зеркал приводит к заметной деформации формы моды по отношению к рассчитанной в рамках модели бесконечной апертуры. При этом имеет место быстрый рост дифракционных потерь моды с уменьшением числа Френеля. В области Nфр³ 10 потери имеют незначительную величину. При этом распределения полей собственных мод резонатора хорошо описываются эрмито-гауссовыми или лагерро-гауссовыми функциями.

Несмотря на широкую область применений устойчивых резонаторов, они обладают одним очень серьезным недостатком. Он состоит в весьма малых поперечных размерах основной моды, что связано с фокусирующим действием лазерных зеркал. Так, при длине резонатора порядка 1м и для длины волны, лежащей в видимом диапазоне спектра, радиус пучка основной моды имеет порядок 1мм. В неустойчивых резонаторах, g-факторы которых меняются в областях g1g2>1 и g1g2>0, поле не фокусируется вблизи оси и с хорошим приближением распределение его амплитуды можно считать однородным, а волновой фронт сферическим. Однако, в случае неустойчивых резонаторов, возникает другая проблема, которая связана с тем, что лучи стремятся покинуть резонатор, увеличивая потери энергии. Тем не менее этот факт можно использовать даже в качестве преимущества, если эти лучи, уходящие из резонатора, включить в полезное выходное излучение лазера.

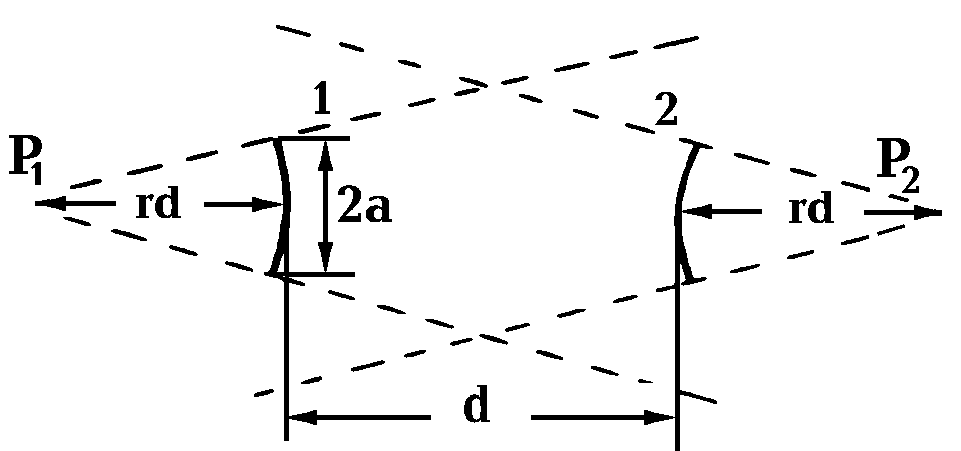
Для описания полей в неустойчивых резонаторах в силу более медленного, чем в устойчивых зонаторах, поперечного изменения амплитуды и фазы вполне подходит геометрооптическое приближение. Рассмотрим симметричный двуторцовый неустойчивый резонатор (рис. 2.2.6). Как и прежде, будем предполагать, что мода образована суперпозицией двух сферических волн постоянной интенсивности. Центры Р1 и Р2, из которых исходят эти волны, не совпадают с центрами кривизны зеркал 1 и 2, но их координаты нетрудно вычислить, используя следующий принцип самосогласования: сферическая волна, исходящая из точки Р1, после отражения от зеркала 2 должна давать сферическую волну, выходящую из точки Р2, и наоборот. Чисто геометрическое рассмотрение приводит к следующему выражению для показанной на рис. 2.2.6 величины r:

. (2.2.38)

Нетрудно видеть, что после того, как пучок пройдет от одного зеркала до другого, размер пятна от каждой сферической волны увеличивается в М раз, причем величина М определяется выражением

. (2.2.39)

Величину М называют однопроходным коэффициентом увеличения. Считая поперечное распределение освещенности однородным, потери за один проход можно записать в виде

, (2.2.40)

где S1 и S2 - площади поперечного сечения пучка, исходящего из точки Р1, соответственно на зеркалах 1 и 2.

Резонатор, показанный на рис. 2.2.6 , редко используется на практике. Гораздо шире применяются асимметричные конфокальные резонаторы. Одна из возможных конфигураций такого резонатора приведена на рис. 2.2.7.

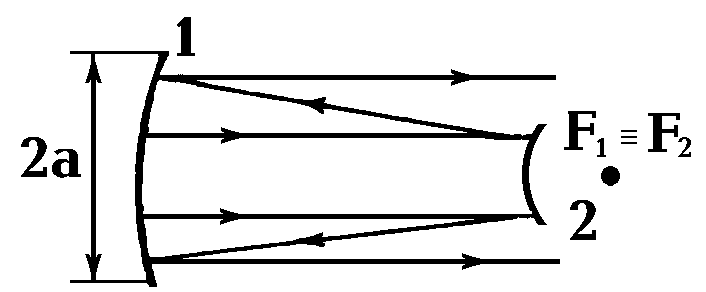
Мода неустойчивого конфокального резонатора представляет собой суперпозицию сферической волны, исходящей из общего фокуса и плоской волны. Лучи последней, покидая резонатор, формируют на выходе узконаправленное излучение. Таким образом, помимо хорошего заполнения активного вещества излучением неустойчивые резонаторы обеспечивают малую угловую расходимость выходного излучения, приближающуюся к дифракционному пределу.

Вышеприведенное рассмотрение свойств оптических резонаторов основывалось на предположении, что активная среда, находящаяся внутри резонатора, не вносит существенных искажений в структуру собственных мод. Накопленный в настоящее время обширный экспериментальный материал подтверждает справедливость этого предположения для широкого класса лазеров. Однако в ряде случаев, когда распределение показателя преломления и коэффициента усиления в сильной степени неоднородно, следует учитывать влияние активной среды. Поскольку неоднородности активной среды чаще всего носят квадратичный характер, для их учета следует владеть теорией распространения света в квадратичных средах. Основы этой теории приведены в разделе 2.3.1.

Как следует из разделов 2.2.2 и 2.2.3, в общем случае в лазерном резонаторе может возбуждаться большое число мод, отличающихся как продольными, так и поперечными индексами. Многомодовый характер генерации существенным образом усложняет пространственные характеристики и спектральные характеристики излучения. На практике обычно не составляет труда выделить одну поперечную моду. Так, основная мода ТЕМ00 легко выделяется помещением в резонатор диафрагмы, размеры которой обеспечивают подавление всех высших мод. Однако даже в случае генерации лазера на основной моде в контур рабочей линии усиления попадает, как правило, большое число частот. Для того, чтобы улучшить монохроматичность излучения, необходимо проводить селекцию продольных мод, что представляет задачу гораздо более сложную. В настоящее время разработан целый ряд способов селекции продольных мод. Целесообразность применения каждого из них определяется конкретными свойствами лазерной среды и требованиями, предъявляемыми к спектральному составу генерации. Все существующие методы основаны на создании таких условий, когда минимальными потерями будут обладать моды, частоты которых располагаются в узком спектральном интервале. Эти моды будут присутствовать в спектре генерации, остальные же будут подавляться из-за недостатка усиления. Мы ограничимся качественным описанием некоторых резонаторных устройств, позволяющих селектировать продольные моды.

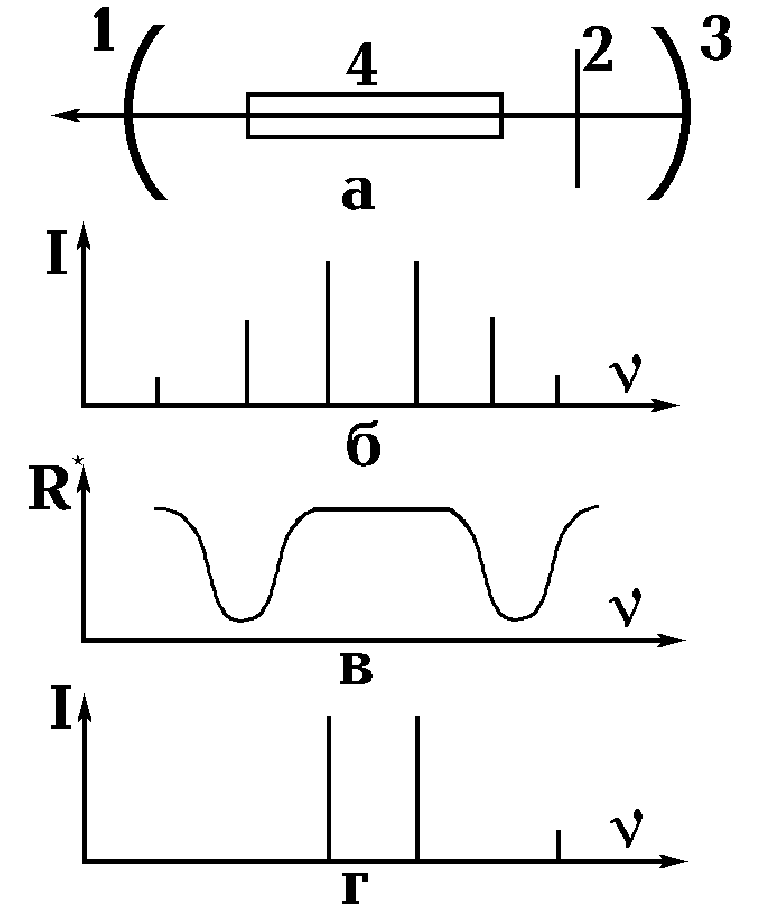
Связанные резонаторы. Уже на начальном этапе развития лазерной техники было обнаружено, что селектирующими свойствами обладает система из двух оптических связанных открытых резонаторов. Простейшей системой такого типа является трехзеркальная система, схема которой приведена на рис. 2.2.8, а. Зеркала 1 и 2 формируют основной резонатор с активным веществом 4, зеркала 2 и 3 - дополнительный. Выходное зеркало 1 и среднее зеркало 2 выполнены полупрозрачными. Возможность селекции частот в такой системе легко объяснима, если интерферометр, образованный зеркалами 2 и 3, рассматривать как единый отражатель, эффективный коэффициент

отражения которого R* зависит от частоты n . Эта зависимость, фактически характеризующая отражательную способность интерферометра Фабри-Перо, хорошо известна и качественно приведена на рис. 2.2.8, в. Расстояние между соседними минимумами связано с длиной дополнительного резонатора dg соотношением D n =с/2dg. Их же ширина увеличивается с ростом коэффициента пропускания зеркала 2. Генерация будет иметь место на частотах, соответствующих максимальным значениям R*. Если в отсутствии зеркала 3 спектр генерации имел вид, показанный на рис. 2.2.8, б, то в трехзеркальной схеме происходит его сужение (рис. 2.2.8, г). Поскольку спектральный интервал, где R* принимает высокие значения, довольно большой, селектирующая способность трехзеркальной системы невелика.

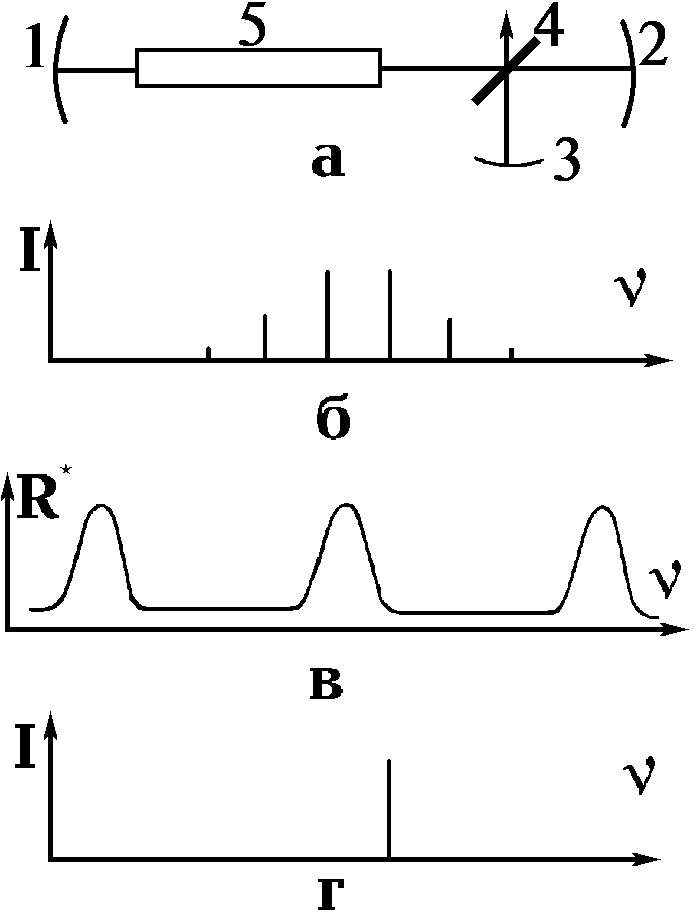
Существенно более хорошими селектирующими свойствами обладает так называемая система Смита, показанная на рис. 2.2.9, а.

Основной резонатор этой системы, образованный зеркалами 1, 2, содержит активное вещество 5. Дополнительный резонатор сформирован зеркалами 2, 3, а также полупрозрачной пластиной 4, располагающейся внутри основного резонатора. Как и в предыдущем случае, зеркала 2, 3 и пластину 4 можно рассматривать как единый отражатель с изменяющимися по частоте эффективным коэффициентом отражения R*. Принципиальное отличие системы Смита от трехзеркальной системы состоит в том, что поведение R* совпадает с максимумом внутрирезонаторной мощности. Зависимость R*(n ) приведена на рис. 2.2.9, в. Так как область максимальных значений R* сужается, то, как видно из рис. 2.2.9, б и г, селектирующая способность улучшается, и появляется возможность реализовать одночастотный режим генерации.

Резонаторы с поглощающей пленкой. Селективность резонаторов, содержащих помещаемую между зеркалами поглощающую пленку, обусловлена эффектом подавления тех продольных мод, пучности стоячих волн которых внутри резонатора совпадают с положением пленки. Этот эффект иллюстрирует рис. 2.2.10, где показана структура поля стоячих волн внутри резонатора. Пунктир соответствует подавляемой моде, непрерывные кривые характеризуют структуру стоячей селектируемой моды. Узел ее поля совпадает с пленкой, и в отличие от других продольных мод она будет испытывать минимальные потери.

Резонаторы с дисперсионными элементами. Весьма эффективный способ сужения спектра лазерной генерации основан на использовании в лазерном резонаторе элементов, коэффициенты пропускания которых характеризуются резко выраженными зависимостями от частоты световых колебаний. Чаще всего в роли таких элементов используются дифракционные решетки и наклонные интерферометры Фабри-Перо. На рис. 2.2.11. Изображен лазер, резонатор которого содержит такие элементы. Дифракционная решетка в нем одновременно выполняет функции резонаторного зеркала. Наличие в резонаторе наклонного интерферометра позволяет дополнительно сузить спектральный интервал, выделяемый дифракционной решеткой. Достоинством приведенной схемы является возможность простым вращением решетки перестраивать частоту генерации лазера.

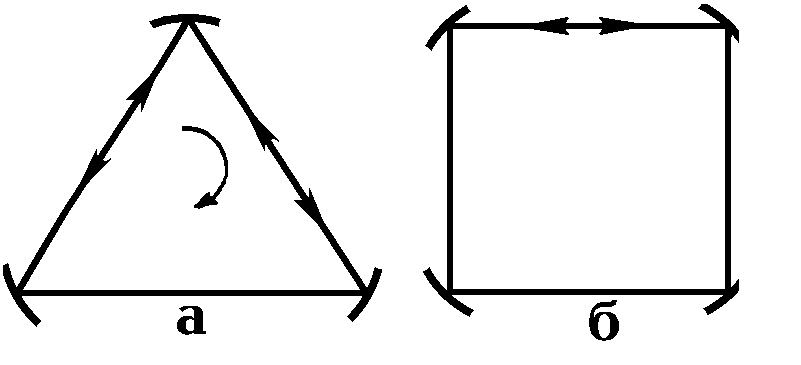
Все вышеперечисленные резонаторы объединены тем свойством, что в них формируются стоячие волны. Существуют, однако, такие резонаторы, энергия в которых накапливается в виде энергии бегущих волн. К ним, в первую очередь, следует отнести так называемые кольцевые резонаторы, подобные изображенным на рис. 2.2.12. Осевым контуром кольцевого резонатора принято называть луч, который, испытав отражения от резонаторных зеркал, замыкается сам на себя.

Траектория этого луча представляет собой ломаную линию, лежащую в некоторой плоскости, называемой плоскостью контура резонатора. Вдоль контура резонатора, навстречу друг другу, распространяются две бегущие волны. Рассматривая движение гауссова пучка по контуру и приравнивая его фазовый набег за один оборот целому числу p, можно аналогично тому, как было сделано в разделе 2.2.2 для линейного резонатора, найти параметры пучка с самосогласованными параметрами, являющегося собственной модой резонатора. Единственной особенностью является астигматизм, проявляющийся при отражении пучка от сферического зеркала. Наличие астигматизма приводит к тому, что радиусы пучков в плоскости контура резонатора и в перпендикулярной ей плоскости оказываются различными. Расчет, выполненный для симметричного трехзеркального кольцевого резонатора (см. рис. 2.2.12,а), показывает, что перетяжки собственной моды резонатора расположены на серединах сторон треугольника. При этом минимальный радиус пучка в плоскости контура резонатора

, (2.2.41)

а в перпендикулярной плоскости

, (2.2.42)

где а - сторона треугольника, R - радиус кривизны зеркал. Спектр собственных частот такого резонатора определяется формулой

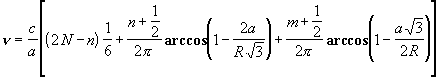. (2.2.43)

Здесь n - определяет число нулей поля в плоскости контура, а m - в перпендикулярной плоскости.

Кольцевые резонаторы нашли широкое применение в лазерных гироскопах. Принцип работы последних основан на различии путей волн, распространяющихся по и против часовой стрелки, в случае вращения резонатора вокруг оси, перпендикулярной плоскости контура (рис. 2.2.12, а). Это различие является непосредственным следствием известного из специальной теории относительности эффекта сокращения линейных размеров тел при движении. Разница в оптических путях приводит к относительным сдвигам частот встречных волн и возникновению между ними биений. По частоте же биений можно судить об угловой скорости вращения гироскопа.

Создание мощных лазеров требует использования больших объемов активного вещества. В то же время увеличение размеров активной зоны лазера, как правило, приводит к снижению качества излучения из-за расширения модового состава генерации и усугубляющегося негативного влияния неоднородностей лазерно-активной среды. Один из вариантов решения проблемы сочетания требований качества и мощности излучения состоит в использовании так называемой модульной лазерной системы. Активный модуль такой системы состоит из сборки малоапертурных активных элементов, количество которых может достигать нескольких десятков, а в некоторых случаях и нескольких сотен. На рис. 2.2.13 приведена упрощенная двумерная схема сборки активных элементов (обычно применяется трехмерная, объемная сборка с существенно большими количеством элементов). Сборка помещена в плоскопараллельный резонатор, образованный зеркалами М1 и М2. В силу небольшой апертуры активных элементов через них без существенных потерь будут распространяться световые пучки, сформированные лишь низшими модами с невысокой угловой расходимостью. Если сборка включает N активных элементов, то направляемая на мишень мощность, выходящая из резонатора модульной системы, оказывается в N раз больше плотности мощности, получаемой от отдельного элемента. Этот результат соответствует случаю, когда из-за несфазированности световых колебаний в отдельных элементах, выходящее из модульной системы излучение является некогерентным.

Иная ситуация имеет место, если генерация в отдельных модулях сфазирована и излучение когерентно. В этом случае максимальная плотность мощности на мишени оказывается в N2 раз больше, чем для отдельнного элемента. Для того, чтобы обеспечить последний, несомненно, более выгодный режим работы лазерной модульной системы, необходимо ввести оптическую связь между элементами сборки. Такую связь, в принципе, можно обеспечить, направляя с помощью системы дополнительных полупрозрачных зеркал часть излучения от каждого элемента в соседний. Однако, при большом числе элементов в сборке такой способ оказывается слишком громоздким и сложным в осуществлении.

Весьма эффективным оказался иной подход к осуществлению оптической связи, использующий эффект Талбота (см. п. 1.2.4). Этот эффект может быть использован, если расположение элементов в сборке будет носить строго регулярный, периодический характер. Такая сборка может рассматриваться в виде периодической решетки. Согласно эффекту Талбота, при когерентном излучении периодической решетки существует расстояние zq, на котором структура решетки будет воспроизводиться. Отсюда ясно, что, располагая одно из плоских зеркал резонатора на расстоянии zq/2 от сборки, можно обеспечить возвращение излучения, дифрагировавшего на торцах элементов, в каждый элемент. Необходимая оптическая связь между отдельными каналами модуля достигается при этом за счет дифракционного перераспределения световой энергии в возвращенном пучке. Поскольку режим генерации с самовоспроизводящимся по эффекту Талбота полем характеризуется большей добротностью резонатора, лазерная модульная система с резонатором, построенным по схеме рис. 2.2.13, будет генерировать когерентное излучение с высокой плотностью мощности в дальней зоне.