ГЛАВА 2. ФОРМИРОВАНИЕ И РАСПРОСТРАНЕНИЕ ВОЛНОВЫХ ПУЧКОВ
В настоящее время наиболее распространенным источником когерентного излучения является лазер. Как правило, лазер генерирует излучение в виде слабо расходящегося волнового пучка, размеры которого в поперечной плоскости велики по сравнению с длиной волны. Настоящая глава посвящена анализу процессов формирования и распространения узконаправленных пучков лазерного излучения. Центральным понятием излагаемой теории является понятие моды - такого волнового пучка, который сохраняет в процессе распространения форму распределения амплитуды и фазы световых колебаний в поперечном сечении.
2.1 Моды свободного пространства [1-5]
2.1.1 Параболическое приближение
Волновой лазерный пучок в силу своей высокой направленности имеет много общего с плоской волной. Отличие же его от плоской волны состоит в том, что распределение интенсивности в нем неоднородно (мощность пучка, в основном, сконцентрирована вблизи оси), а фазовый фронт несколько отличается от плоского. Поэтому решение приведенного волнового уравнения, описывающее распространение такого пучка, будем искать в виде
![]() , (2.1.1)
, (2.1.1)
где u(x,y,z) - медленно меняющаяся комплексная функция, которая и определяет свойства лазерного пучка, отличающие его от плоской волны. Быстрые осцилляции по z обусловлены присутствием в (2.1.1) экспоненциального множителя. Применяя оператор D к функции Y , имеем
![]()
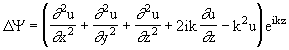 . (2.1.2)
. (2.1.2)
Если в выражении (2.1.2) пренебречь второй производной u по z по сравнению c первой, то на основании (1.2.20) получим уравнение
![]() . (2.1.3)
. (2.1.3)
Полученное уравнение относится к уравнениям параболического типа, а само приближение, в рамках которого оно было получено, называется параболическим приближением. Нетрудно показать, что уравнению (2.1.3) будет удовлетворять так называемый гауссов пучок, амплитуда которого меняется по поперечной координате по гауссовому закону.
2.1.2 Свойства основной моды
Для гауссова пучка можно записать выражение
![]() , (2.1.4)
, (2.1.4)
где ![]() . Параметр Р - комплексный фазовый сдвиг при распространении света вдоль оси z, а q - комплексный параметр пучка, определяющий гауссово распределение поля по координате r, где r - расстояние от оси. Кроме того, q определяет кривизну волнового фронта, который вблизи оси является сферическим. Подставив выражение (2.1.4) в (2.1.3), получим
. Параметр Р - комплексный фазовый сдвиг при распространении света вдоль оси z, а q - комплексный параметр пучка, определяющий гауссово распределение поля по координате r, где r - расстояние от оси. Кроме того, q определяет кривизну волнового фронта, который вблизи оси является сферическим. Подставив выражение (2.1.4) в (2.1.3), получим
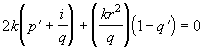 . (2.1.5)
. (2.1.5)
Штрих означает производную по z. Уравнение (2.1.5) эквивалентно двум уравнениям
![]() , (2.1.6)
, (2.1.6)
![]()
![]() . (2.1.7)
. (2.1.7)
Интегрируя (2.1.6), получаем
![]() . (2.1.8)
. (2.1.8)
Это уравнение устанавливает весьма простое соотношение между параметром пучка в разных сечениях, отстоящих друг от друга на расстоянии z.
Когерентный световой пучок с гауссовым распределением поля имеет фундаментальное значение в теории волновых пучков. Этот пучок называют основной модой в отличие от других мод более высокого порядка, которые будут рассматриваться ниже. Вследствие особой важности рассмотрим свойства гауссова пучка с длиной волны l более подробно. Для этого выразим комплексный параметр q через два действительных параметра пучка R и w
![]() . (2.1.9)
. (2.1.9)
Физический смысл этих параметров становится ясным при подстановке соотношения (2.1.9) в (2.1.4). Видно, что R есть радиус кривизны волнового фронта, а w характеризует изменение поля Е в поперечной плоскости. Распределение поля в этой плоскости, как видно из рис. 2.1.1, подчиняется закону Гаусса и w равно расстоянию, на котором амплитуда поля убывает в е раз по сравнению с полем на оси.
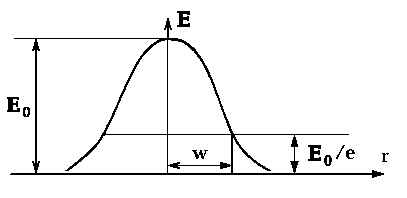
Важно отметить, что гауссов характер распределение поля будет иметь в любой плоскости, будет меняться лишь ширина этого распределения. Параметр w принято называть радиусом пучка, а 2w - диаметром пучка. В некоторой плоскости, называемой горловиной пучка, гауссов пучок стягивается к минимальному диаметру 2w0. В этой плоскости, от которой целесообразно отсчитывать расстояние z, фазовый фронт является плоским и комплексный параметр пучка становится чисто мнимым
![]() . (2.1.10)
. (2.1.10)
На расстоянии z от горловины
![]() . (2.1.11)
. (2.1.11)
Из сопоставления соотношений (2.1.9) и (2.1.11) легко получить следующие важные в практическом отношении выражения:
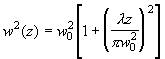 , (2.1.12)
, (2.1.12)
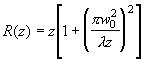 . (2.1.13)
. (2.1.13)
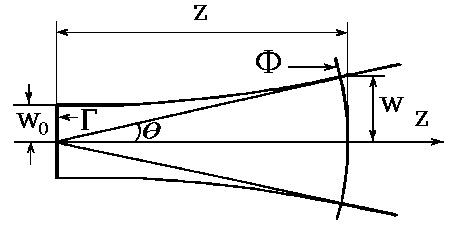
Изменение радиуса, задаваемое выражением (2.1.12), графически иллюстрируется рис. 2.1.2.
Образующая пучка w(z) представляет собой гиперболу, асимптота которой наклонена к оси под углом
![]() . (2.1.14)
. (2.1.14)
Этот угол равен углу дифракции основной моды в дальней зоне.
Для расчета комплексного фазового сдвига на расстоянии z от горловины пучка воспользуемся соотношениями (2.1.7) и (2.1.11); в результате получим
![]() . (2.1.15)
. (2.1.15)
Интегрирование уравнения (2.1.15) дает
![]() . (2.1.16)
. (2.1.16)
Действительная часть Р представляет собой разность фаз Ф между гауссовым пучком и идеальной плоской волной, а мнимая - амплитудный фактор ![]() , который характеризует уменьшение интенсивности на оси из-за расширения пучка. С учетом полученных соотношений выражение (2.1.1) принимает вид
, который характеризует уменьшение интенсивности на оси из-за расширения пучка. С учетом полученных соотношений выражение (2.1.1) принимает вид
![]() , (2.1.17)
, (2.1.17)
где
![]() . (2.1.18)
. (2.1.18)
Из формулы (2.1.18) видно, что Ф растет с увеличением z и уменьшением минимального радиуса пучка ![]() . Максимальное значение Ф равно p
/2. Наличие в показателе экспоненты выражения (2.1.17) члена
. Максимальное значение Ф равно p
/2. Наличие в показателе экспоненты выражения (2.1.17) члена ![]() обусловлено отставанием по фазе световых колебаний на периферии гауссова пучка из-за кривизны волнового фронта.
обусловлено отставанием по фазе световых колебаний на периферии гауссова пучка из-за кривизны волнового фронта.
2.1.3. Моды высших порядков
В предыдущем параграфе рассматривалось лишь одно решение уравнения (2.1.3), а именно гауссов пучок, являющийся основной модой свободного пространства. Существуют, однако, и другие решения уравнения (2.1.3), которым соответствуют пучки с сохраняющейся формой распределения амплитуды поля по поперечному сечению - высшие моды свободного пространства. Все решения (2.1.3) образуют полную ортогональную систему функций, поэтому любое произвольное распределение монохроматического поля может быть разложено по модам свободного пространства.
В прямоугольной системе координат x, y, z решение уравнения (2.1.3) может быть записано в виде
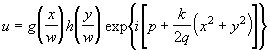 , (2.1.19)
, (2.1.19)
где g - функция x и z, а h - функция y и z. Для действительных g и h это решение описывает моды, поперечное распределение поля которых связано с радиусом гауссова пучка w(z). Подставляя (2.1.19) в (2.1.3), можно убедиться, что функция g и h удовлетворяют тому же самому дифференциальному уравнению, что и полиномы Эрмита Hn(t)
![]() , (2.1.20)
, (2.1.20)
где n - целое число, а ![]() для функции g и
для функции g и ![]() для функции h. Таким образом
для функции h. Таким образом
![]() , (2.1.21)
, (2.1.21)
где m, как и n - целое число.
Физический смысл индексов m и n, называемых поперечными индексами моды, заключается в том, что они показывают, сколько раз поле меняет знак соответственно в направлении x и y. Важно отметить, что моды всех порядков характеризуются одним и тем же масштабным параметром w(z). Полиномы Эрмита низших порядков равны
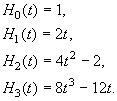
Для математического описания мод более высоких порядков можно использовать выражение (2.1.17), если в правую его часть вставить произведение ![]() . Распределение поля в модах свободного пространства будет определяться, таким образом, произведением функций Эрмита и Гаусса
. Распределение поля в модах свободного пространства будет определяться, таким образом, произведением функций Эрмита и Гаусса
![]() (2.1.22)
(2.1.22)
В частном случае m=0, n=0 мы имеем гауссов пучок - основную моду свободного пространства. Параметр R(z) в (2.1.22) для всех мод одинаков. Это означает, что кривизна волнового фронта одинакова для всех мод и закон его изменения один и тот же. Однако фазовый сдвиг Ф зависит от поперечного индекса. Можно найти, что
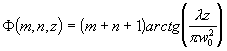 . (2.1.23)
. (2.1.23)
Из выражения (2.1.23) видно, что фазовая скорость с ростом индекса увеличивается.
Если решать уравнение (2.1.3) в цилиндрической системе координат r, j , z, подобное решение записывается в виде
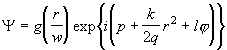 . (2.1.24)
. (2.1.24)
После некоторых преобразований можно получить
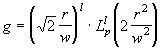 , (2.1.25)
, (2.1.25)
где ![]() - обобщенный полином Лагерра, а р и l - соответственно угловой и радиальный индексы, показывающие, сколько раз поле меняет знак в радиальном и азимутальном направлениях.
- обобщенный полином Лагерра, а р и l - соответственно угловой и радиальный индексы, показывающие, сколько раз поле меняет знак в радиальном и азимутальном направлениях.
Полиномы Лагерра низших порядков равны:
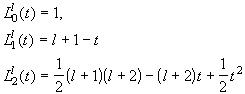
В цилиндрической системе координат, тем самым, моды будут описываться лагерро - гауссовыми функциями
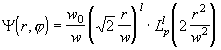
![]() . (2.1.26)
. (2.1.26)
Как и для случая прямоугольных координат, параметры w и R одинаковы для всех цилиндрических волн, а разность фаз, как и ранее, зависит от индексов моды и определяется уравнением
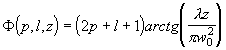 (2.1.27)
(2.1.27)
Графические распределения амплитуды поля для некоторых низших мод приведены на рис. 2.1.3. Для наглядности под каждым графиком приведена картина, наблюдаемая на экране при падении на него светового пучка, соответствующего определенной моде.
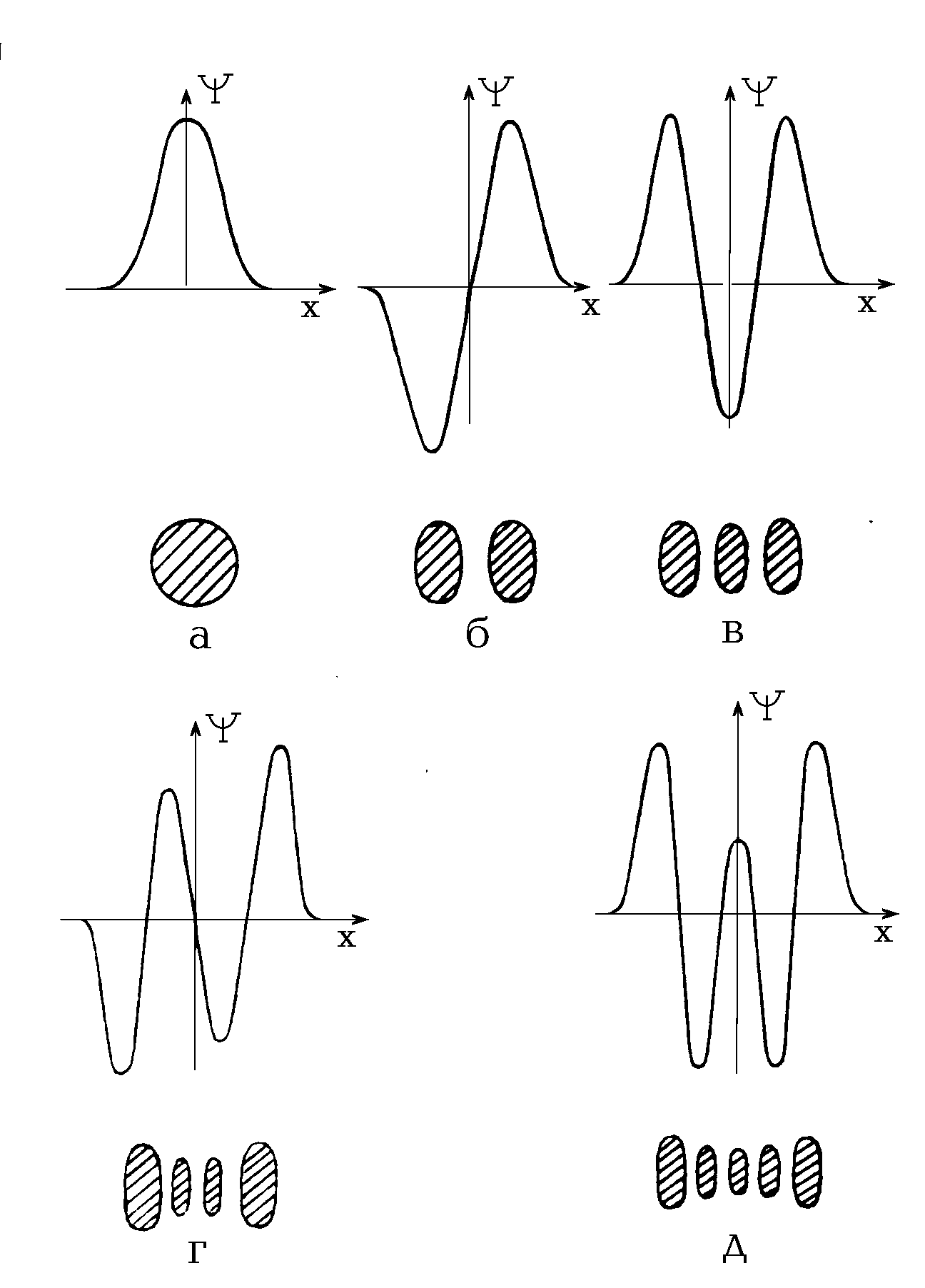
Как эрмито-гауссовые, так и лагерро-гауссовые моды, реализуемые на практике, характеризуются, как правило, большим значением радиуса кривизны волнового фронта. Поэтому их с хорошей степенью приближения можно отнести к поперечным электромагнитным волновым пучкам вида ТЕМ. С учетом поперечных индексов эти пучки часто обозначаются как пучки ТЕМmn или ТЕМpl.
Следует, однако, помнить, что световые поля, записанные в виде (2.1.22) и (2.1.26), являются лишь приближенными решениями волнового уравнения. Степень приближения ухудшается с увеличением чисел (m+n) или (2p+l) и решение перестает быть верным, если величина, содержащая в качестве сомножителя сумму m+n+1 (либо 2p+l+1) становится сравнимой со значением kz. Представление же произвольного поля в виде разложения по модам (2.1.22) и (2.1.26) является, следовательно, не строгим, а приближенным решением волнового уравнения. Если члены высокого порядка дают заметный вклад в разложение, то, чтобы ряд в целом был решением волнового уравнения, необходимо вводить дополнительные коэффициенты к членам ряда.
2.1.4. Преобразование волновых пучков с помощью линз
Как известно, линзы широко применяются либо для фокусировки лазерного пучка в пятна небольших размеров, либо для соответствующего преобразования диаметра и кривизны волнового фронта пучка с целью ввода в данную оптическую систему. Идеальная линза или система линз не изменяет поперечного распределения поля моды свободного пространства. Иначе говоря, входная основная гауссова мода после прохождения линзовой системы сохраняется, а моды высших порядков преобразуются на выходе в моды тех же порядков. Однако при этом параметры мод R(z) и w(z) претерпят изменения. Рассмотрим соотношение между входными параметрами, обозначаемыми индексом 1, и соответствующим выходными параметрами с индексом 2.
Идеальная тонкая линза с фокусным расстоянием f преобразует сферическую волну радиуса R1, слева от линзы в сферическую волну с радиусом R2 справа так, что
![]() . (2.1.28)
. (2.1.28)
Это преобразование поясняется рис.2.1.4. Радиус кривизны считается положительным, когда волновой фронт выпуклый, если смотреть из точки z® ¥ . Линзовая система преобразует волновой фронт моды так же, как и сферическую волну. Если линза тонкая и диаметр пучка слева и справа от нее одинаков, то соотношение между комплексными параметрами входного и выходного пучка запишется по аналогии с (2.1.28) в виде
![]() , (2.1.29)
, (2.1.29)
где q1,2 измерены непосредственно у линзы.
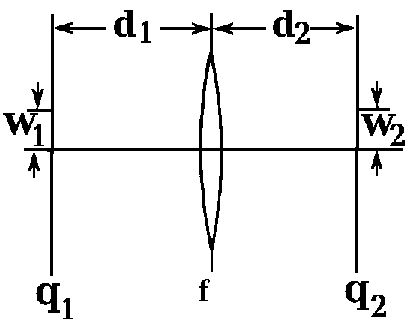
Если же q1 и q2 измерять на расстоянии d1 и d2 от линзы, как показано на рис. 2.1.5, то соотношение между ними принимает вид
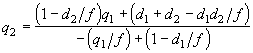 (2.1.30)
(2.1.30)
Эта формула получается непосредственно из выражений (2.1.8) и (2.1.9).
Более сложные оптические системы, такие, как комбинация линз, газовые линзы или толстые линзы, следует рассматривать как последовательность тонких линз, расположенных на различных расстояниях. Для расчета прохождения пучка лазера через сложные системы, таким образом, достаточно последовательного приложения к системе соотношений (2.1.28) и (2.1.29).
2.1.5. Геометрооптическое описание распространения и преобразования волновых пучков
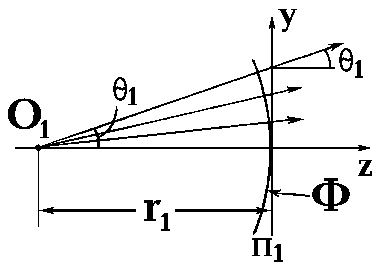
Решение многих важных в практическом отношении задач существенным образом упрощается, если воспользоваться связью, которая существует между оптикой гауссовых пучков и геометрической оптикой. Сферическому волновому фронту гауссова пучка в любом поперечном сечении можно поставить в соответствие пучок лучей, исходящих из одной и той же точки О1 (рис. 2.1.6).
Для каждого параксиального луча отношение координаты y1 точки его пересечения с плоскостью П1 к лучевому углу q 1 равно r1, т.е.
![]() . (2.1.31)
. (2.1.31)
Кривизну волнового фронта считают положительной, когда волна расходится. При этом для радиуса кривизны фронта принято использовать “приведенное значение” ![]() , где n - показатель преломления среды,
, где n - показатель преломления среды, ![]() . Использование приведенных значений удобно тем, что при пересечении пучком границы раздела двух сред значение R не изменяется.
. Использование приведенных значений удобно тем, что при пересечении пучком границы раздела двух сред значение R не изменяется.
Рассмотрим, как преобразуется радиус кривизны R при прохождении пучком некоторой оптической системы. Пусть входная плоскость этой системы совпадает с плоскостью П1; выходную же обозначим через П2. Параметры любого луча из рассматриваемого лучевого пучка будут преобразовываться системой в соответствии с соотношениями
![]() , (2.1.32)
, (2.1.32)
![]() . (2.1.33)
. (2.1.33)
Параметры y2 и v2 соответствуют плоскости П2. Величины A, B, C, D характеризуют конкретную оптическую систему. Уравнения (2.1.32) и (2.1.33) можно записать в матричной форме
![]() , (2.1.34)
, (2.1.34)
где матрица ABCD является матрицей передачи луча. Разделим уравнение (2.1.32) на уравнение (2.1.33)
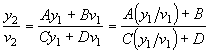 . (2.1.35)
. (2.1.35)
Заменяя значения y/v на R, получаем следующее важное соотношение, связывающее значения приведенного радиуса на выходе и входе системы
![]() . (2.1.36)
. (2.1.36)
Преобразование (2.1.36) называют правилом ABCD. Поскольку преобразование оптическими элементами параметра гауссова пучка q аналогично преобразованию радиуса кривизны волнового фронта R, правилу ABCD можно придать вид
![]() . (2.1.37)
. (2.1.37)
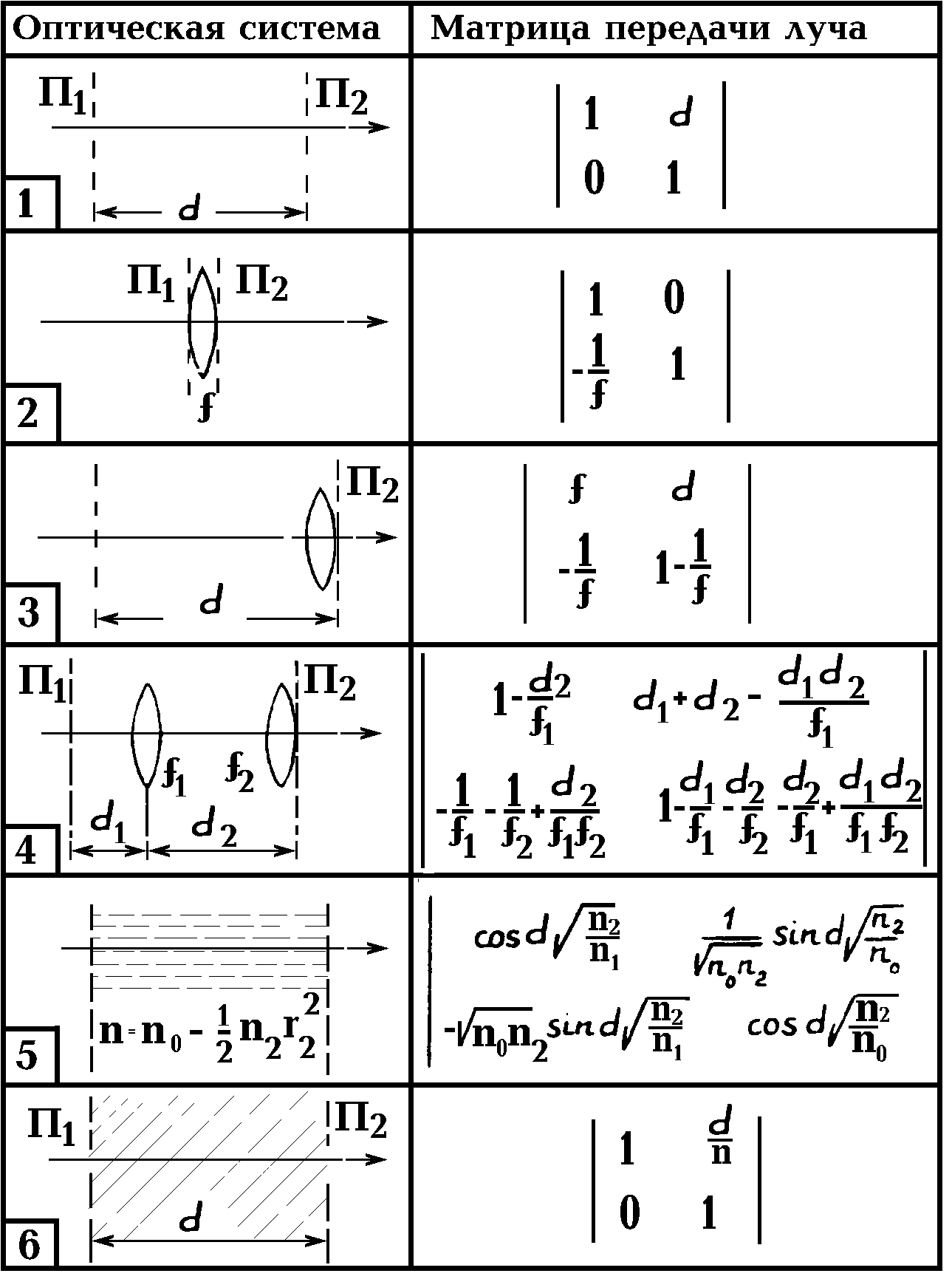
Тем самым, зная матрицу передачи луча, можно в соответствии с (2.1.37) определить трансформацию гауссова пучка той или иной оптической системой. Так как матрицы передачи луча рассчитаны в настоящее время для многих оптических систем, использование правила ABCD существенным образом упрощает описание происхождения гауссовых пучков через различные среды и устройства. Матрицы передачи светового луча для шести простейших оптических систем приведены в табл. 2.1.1. Плоскости П1 и П2 помечены пунктиром. Матрица № 1 описывает прохождение луча в свободном пространстве на расстоянии d, матрица № 2 - прохождение луча через тонкую линзу с фокусным расстоянием f. Матрица № 3 представляет собой комбинацию первых двух. Последовательное соединение двух систем типа № 3 описывается матрицей № 4, которая получается простым перемножением матриц. Под номером 5 представлена матрица передачи луча для линзоподобной квадратичной по показателю преломления n среды длиной d. Матрица № 6 соответствует диэлектрику с показателем преломления n и длиной d. Сравнивая матрицы № 1 и № 6, можно заметить, что оптически более плотная среда уменьшает эффективную длину пути параксиальных лучей, хотя, как известно, оптическая длина пути увеличивается.
Геометрооптические методы расчета характеристик эрмито-гауссовых или лагерро-гауссовых пучков, распространяющихся в оптических системах, широко используются в современной оптике. Обширная практика их применения, многократные сопоставления результатов расчетов с экспериментальными данными, не оставляют сомнений в их правильности и эффективности.
Однако приведенное выше физическое обоснование указанных методов, апеллирующее к сходству изменений комплексного параметра гауссова пучка q и радиуса кривизны волнового фронта R, нельзя считать достаточно строгим. Более последовательное и строгое доказательство применимости геометрического подхода можно осуществить, используя формализм расчета полей от источников, расположенных в комплексной плоскости. В рамках этой теории, с которой можно более подробно ознакомиться по монографии [5], гауссов пучок оказывается эквивалентным волне от точечного источника, расположенного в точке с координатами (0,0,-ib), где i - мнимая единица, b=p w02il . "Сферический характер" такой волны делает более наглядным сходство преобразования в отических системах сферических волн и гауссовых пучков.
2.1.6. Расчет поля дифрагированной волны методом разложения по модам свободного пространства
Скалярная теория дифракции, рассмотренная в первой главе, дает универсальный подход расчета поля дифракции волновых пучков на различного рода препятствиях. Однако составленные на основе дифракционных интегралов программы машинного расчета поля дифракции для ближней и дальней зон весьма сложны и имеют существенные отличия.
Свойство ортогональности мод свободного пространства дает возможность использовать для расчета поля дифракции иной подход, основанный на разложении поля пучка, претерпевающего дифракцию, по модам свободного пространства. Оно во многих случаях оказывается более простым и позволяет на основе одного алгоритма рассчитывать поля в ближней и дальней зонах дифракции. Этот метод особенно эффективен в случае слабого дифрагирования лазерных пучков. Плавный профиль изменения амплитуды лазерного пучка в плоскости апертурного разложения позволяет исключить в разложении моды со слишком высокими индексами, что сокращает время расчета и повышает его точность.
Пусть лазерная волна падает на отверстие произвольной формы в непрозрачном экране. Будем считать, что поперечное распределение амплитуды поля пучка в полярных координатах определяется функцией u(r,j ). Представим поле дифрагировавшей волны в виде суперпозиции лагерро-гауссовых ТЕМpl-мод свободного пространства (p,l - радиальный и угловой индексы соответственно), поперечное распределение поля которых характеризуется нормированными ортогональными функциями y pl. Тогда амплитуду светового поля uD(r,j ,z) на расстянии z от отверстия можно представить в виде ряда
![]() (2.1.38)
(2.1.38)
ось z совпадает с направлением распространения TEMpl-волн (в плоскости отверстия z=0). Коэффициенты разложения можно найти из соотношения
![]() (2.1.39)
(2.1.39)
где интегрирование ведется по площади отверстия S. Минимальный радиус пучка мод TEMpl в практических расчетах выбирается из соображений быстрой сходимости ряда (2.1.38). Таким образом, алгоритм расчета поля дифракции как в ближней, так и в дальней зонах сводится к двум операциям: нахождению коэффициентов разложения и суммированию амплитуд TEMpl-волн в плоскости наблюдения.
Рассмотрим частный случай нормального падения основной волны лазера ТЕМ00 на на круглую центрированную диафрагму радиуса r0. Световое поле на отверстии описываетс функцией
![]()
![]() (2.1.40)
(2.1.40)
где ![]() - радиус пучка в плоскости отверстия. В силу аксиальной симметрии задачи отличными от нуля будут только те коэффициенты разложения Cp0=Cp, азимутальный индекс которых равен нулю. Переходя к безразмерным параметрам
- радиус пучка в плоскости отверстия. В силу аксиальной симметрии задачи отличными от нуля будут только те коэффициенты разложения Cp0=Cp, азимутальный индекс которых равен нулю. Переходя к безразмерным параметрам ![]() и
и ![]() и используя выражения для y
pl, поперечное распределение интенсивности волны на расстоянии z от диафрагмы можно представить в виде (радиус пучка в плоскости диафрагмы считается минимальным,
и используя выражения для y
pl, поперечное распределение интенсивности волны на расстоянии z от диафрагмы можно представить в виде (радиус пучка в плоскости диафрагмы считается минимальным, ![]() =
=![]() 0)
0)
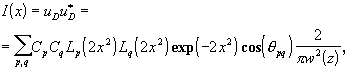 (2.1.41)
(2.1.41)
где
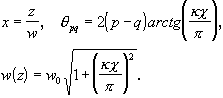
Для улучшения сходимости ряда (2.1.41) целесообразно проводить разложение по модам TEMp0 с минимальным радиусом пучка, равным ![]() , если a
<1, и
, если a
<1, и ![]() =w0, если
=w0, если ![]() ,где
,где ![]() - параметр ограничения пучка.
- параметр ограничения пучка.
Расчеты по формуле (2.1.41)показывают, что приемлемую точность в расчетах можно достичь, не привлекая в разложении моды с индексами p и l,значения которых превышают 10.
| Дальше | К оглавлению |