Возможны две точки зрения на место геометрической оптики в системе современных оптических представлений. Согласно первой из них геометрическая оптика рассматривается как самостоятельный раздел оптики, основанный на определенной системе постулатов. К наиболее важным из них относятся законы прямолинейного распространения света, законы его отражения и преломления. В такой постановке геометрическая оптика является основой вычислительной оптики [11], на базе которой осуществляются расчеты разнообразных оптических элементов и систем. Согласно второй точки зрения основные выражения и соотношения аппарата геометрической оптики являются по своей сути приближенными решениями волновых уравнений, во многих случаях облегчающих их анализ. Исходя из целевой установки данной книги мы будем придерживаться второй точки зрения. При этом сосредоточимся на вопросах распространения света в неоднородной среде, показатель преломления которой плавно меняется в пространстве. Световое поле представляется в форме локально плоской волны. В приближении геометрической оптики амплитуда этой волны не зависит от частоты, а частота, которая считается большой величиной, входит только в фазовый множитель.

В однородной (n=const) среде простейшее решение волнового уравнения - плоская волна

(1.3.1)

Фаза ее постоянна на плоскостях z=cоnst, т.е. фазовые фронты плоские. Нормали к фронтам параллельны.

Пусть показатель преломления среды есть функция координат

n=n(r),

тогда амплитуда А становится функцией координат, а волновые фронты перестают быть плоскими. Нормали к ним не параллельны, но близки к параллельным. Будем считать, что все характерные масштабы изменения и амплитуды поля, и показателя преломления среды велики по сравнению с длиной волны l (l =2p /k). Если l - наименьший из этих масштабов, то предполагается, что выполнено неравенство

(1.3.2)

Это неравенство - не самое сильное условие применимости лучевой или геометрической оптики, законы которой мы ниже сформулируем. Представим поле световой волны в неоднородной среде в виде почти плоской волны

(1.3.3)

Здесь А(k,r) - амплитуда волны; kS(r) - фаза; величина S(r) называется эйконалом. Термин "почти плоская волна" оправдан тем, что в области порядка 2p /kn поле имеет вид.(1.3.1).

Амплитуду А и эйконал S будем искать из требования, чтобы решение, записанное в форме (1.3.3), удовлетворяло волновому уравнению, и при этом используем условие, что k велико. Это можно сделать несколькими способами. Простейший из них состоит в том, чтобы искать А в виде лучевого разложения по обратным степеням k:

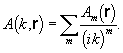(1.3.4).

Фактически это разложение проводится по возрастающим степеням безразмерного малого параметра m (1.3.2).

Подставляя (1.3.3), (1.3.4) в волновое уравнение

(1.3.5)

и приравнивая нулю коэффициенты при одинаковых степенях k, получим в нулевом приближении уравнение эйконала

(1.3.6)

а в следующих приближениях- систему рекуррентных уравнений для амплитуд

(1.3.7)

(1.3.8)

которые называются уравнениями переноса.

Приближение, при котором в (1.3.4) сохраняется только нулевой член, называется геометрооптческим приближением. Поля в этом приближении, т.е. поля геометрической оптики

(1.3.9)

содержат частоту только множителем в фазе. В отличие от (1.3.3), в (1.3.9) А₀ уже не есть функция частоты.

Решение задачи по определению поля в неоднородной среде следует начинать с нахождения эйконала S. Зная эту функцию, можно построить волновые фронты: они задаются уравнением S=const, а затем и лучи - линии, перпендикулярные волновому фронту.

Следует заметить, что вообще эйконал в большей степени определяет световое поле, чем амплитуда А₀ (r). Это объясняется тем, что перед S(k,r) стоит большой множитель k. Поэтому все изменения u при малом изменении координат определяются главным образом изменением S, а не А₀.

Уравнение (1.3.6) решается в наиболее общем виде с помощью метода характеристик. Этот метод сводит уравнение в частных производных к системе обыкновенных дифференциальных уравнений. Обозначим введем параметр t вдоль направления p, связанный с длиной дуги s на луче условием dt =ds /n. Вектор r определяет точку на луче, а вектор dr/dt - касательный лучу. Уравнение (1.3.6) выглядит в новых обозначениях как |p|=n. Можно показать, что оно эквивалентно следующей системе уравнений:

(1.3.10)

(1.3.11)

Уравнения (1.3.10) определяют геометрию лучей

(1.3.12)

т.е. координаты r и направления p луча в точке с параметром t (этот параметр пропорционален времени прохождения волны вдоль луча). Очевидно, что касательный к лучу вектор (1.3.10,а) параллелен Ñ S, т.е. перпендикулярен к волновой поверхности. Таким образом, луч есть нормаль к поверхности равной фазы.

Вектор p, определяющий направление луча, изменяется вдоль луча, согласно (1.3.11,б) в направлении градиента показателя преломления. Иными словами, преломление или рефракция криволинейного луча в неоднородной среде происходит в область возрастания n.

В частном случае однородной среды , так что p=const, и лучи являются прямыми линиями.

Для эйконала из (1.3.11) получаем

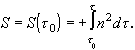(1.3.13)

Здесь - значение эйконала при ; интегрирование ведется вдоль геометрооптического луча. Заметим, что в геометрической оптике физическое значение имеет лишь разность эйконалов , а не величина S.

Для однородной среды

Выбрав направление оси z вдоль луча, умножив затем эйконал - его часто называют "оптический путь" - на частоту k, получим привычное выражение для фазы плоской волны kn(z-z₀), так как, очевидно, в данном случае nt =z.

Для построения лучей и фронтов удобно пользоваться системой лучевых координат (рис. 1.3.1).

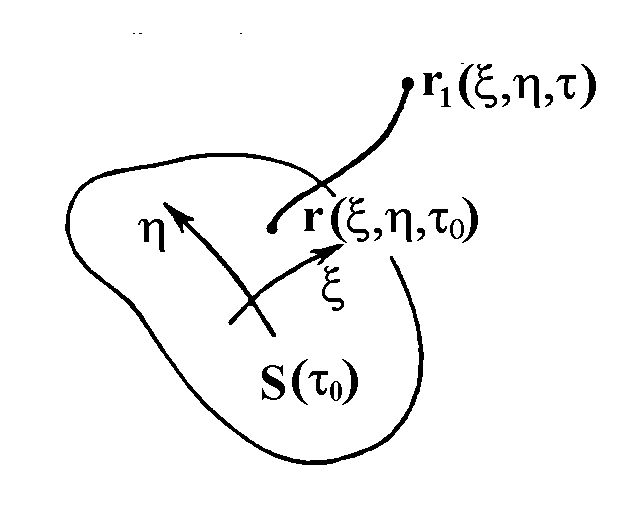
Такими координатами являются две координаты x , h на поверхности любого, принятого за начальный, волнового фронта , характеризующие данный луч и постоянные вдоль луча, и длина дуги s , отсчитываемая вдоль луча, либо вместо s - введенный выше параметр t (время).

Из уравнения эйконала вытекает важное физическое положение, известное, как принцип Ферма, согласно которому оптический луч всегда выбирает траекторию с минимальной длиной оптического пути. Только в очень редких случаях условие минимума заменяется условием максимума. Таким образом, лучевые траектории являются экстремалями функционала Ферма

(1.3.14)

Принцип Ферма определяет лучевую структуру поля не только в плавно неоднородной среде. Луч, соединяющий две точки r₀ и r₁, выделяется из всех кривых, проходящих через эти точки, тем, что эйконал (1.3.13) экстремален. Из принципа экстремальности может быть выведен закон зеркального отражения

(1.3.15)

и закон преломления

(1.3.16)

на резкой границе между двумя плавно-неоднородными средами.

Здесь n₁ - показатель преломления среды, из которой на границу падает луч. Он преобразуется в два луча - преломленный и отраженный в среду n₂. Углы j ₁, j ₂, j ₃ - соответственно углы с нормалью падающего, преломленного и отраженного лучей. Все три луча и нормаль к поверхности расположены в плоскости падения. Хотя эти законы получены для случая падения плоской волны на плоскую границу раздела однородных сред, они выполняются и для неплоской границы между плавно неоднородными средами, если поле сохраняет лучевую структуру (1.3.9).

Перейдем от лучевой структуры поля, т.е. системы волновых фронтов S=const и лучей Ñ S, к определению амплитуд. В лучевых координатах x , h , t уравнения переноса (1.3.7), (1.3.8) сводятся к системе обыкновенных дифференциальных уравнений, и можно выписать в общем виде их решения.

Решение уравнений переноса для двух первых членов ряда (1.3.4) имеет вид:

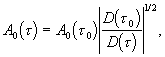(1.3.17)

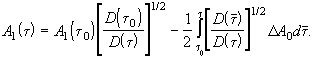(1.3.18)

Здесь

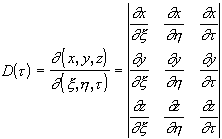(1.3.19)

- якобиан перехода от декартовых координат к лучевым; параметр , вообще говоря, произволен. Якобиан (1.3.19) легко вычисляется, если известны уравнения семейства лучей.

Например, цилиндрическая волна есть геометрооптическое поле, если исключить область порядка l вблизи начала координат. Лучи совпадают с радиусами: под лучевыми координатами x , h , t следует понимать j , z, r/n. D (t )=nr; и 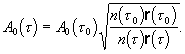Разумеется, цилиндрическая волна может распространятся только в аксиально-симметричной среде (в частности, в среде с постоянным n). В сферически симметричной среде распространяется сферическая волна, здесь координата r отсчитывается от центра волны, так что радиус кривизны волнового фронта R=r . В общем случае поверхности с двумя главными радиусами кривизны .

Определим теперь понятие лучевой трубки. На начальном волновом фронте t = возьмем исходную поверхность s() бесконечно малого размера (рис. 1.3.2).

Лучи, выходящие с контура поверхности, образуют стенки лучевой трубки. Величина пропорциональна отношению площадей элементарной лучевой трубки:

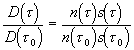, (1.3.20)

и может быть названа расходимостью лучей. Отсюда для нулевого, т.е. геометрооптического, приближения из (1.3.17), (1.3.20) получаем

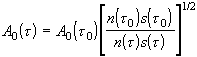. (1.3.21)

Таким образом, в геометрической оптике амплитуда на луче определяется только амплитудой на том же луче в любой точке, откуда этот луч пришел, геометрической расходимостью лучевой трубки и изменением n вдоль луча. Формула (1.3.17), таким образом, означает, что в лучевой трубке сохраняется поток энергии

(1.3.22)

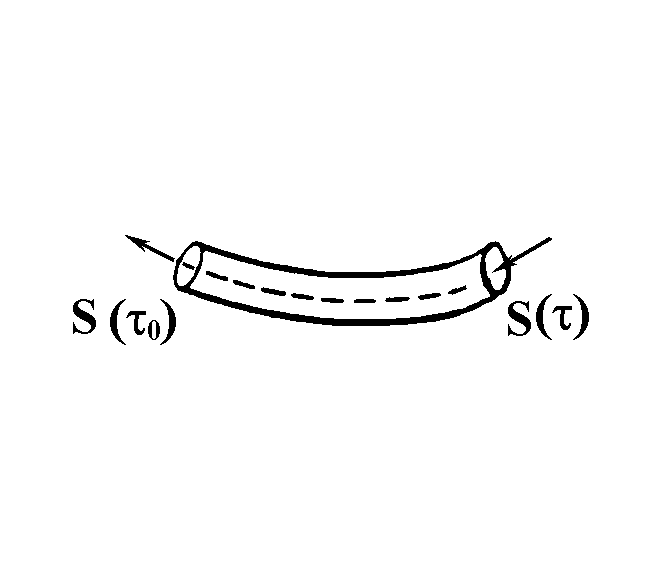
Все лучевое поле можно себе представить состоящим из тонких трубок, причем в каждой трубке распространяется та энергия, которая была в ее начале. Распространение энергии в трубке происходит независимо от соседних. Геометрическая оптика, которая ограничивает ряд (1.3.4) первым членом, допускает, что на протяжении произвольно длинной границы между лучевыми трубками с разной интенсивностью и, в частности, на границе между освещенной областью и теневой - не будет никакого обмена энергией.

Предположение о том, что взаимодействие между лучевыми трубками пренебрежимо мало, может оказаться неверным при продвижении вдоль трубки на достаточно большое расстояние. Действительно, уже для первого коэффициента лучевого разложения А₁ (1.3.18) кроме слагаемого, учитывающего геометрическую расходимость лучей, есть еще интегральное слагаемое, которое содержит производные амплитуды предыдущего приближения А₀. Если бы А₁ и А₀ были величинами одного порядка, то влияние А₁ на суммарное поле, как это следует из лучевого разложения (1.3.4), было бы в k раз меньше, чем влияние А₀. Но эффект взаимодействия между лучевыми трубками из-за интегрального, накапливающегося характера А₁ на достаточно длинном пути может существенно превзойти изменение А₀, связанное с изменением сечения трубки или показателя преломления n вдоль луча.

Итак, геометрическая оптика не дает правильного решения не только в случае, если член лучевого разложения А₁/k становится сравнимым с геометрооптическим членом А₀. Геометрическая оптика не может так же ничего сказать о поле в области тени, куда не проникают лучи. Наконец упомянем третий случай отказа геометрической оптики.

Он относится к ситуации, когда выделенная на заданном волновом фронте лучевая трубка при подходе к некоторой точке схлопывается, т.е. площадь трубки s(t ) становится равной нулю. При этом нулевой член лучевого разложения (1.3.21) становится бесконечно большим. Это означает, что структура поля локально не близка к плоской волне и основные геометрооптические представления теряют свой смысл.

Пусть вдоль луча r₀, r₀ (см. рис. 1.3.3) распространяется световая волна, имеющая геометрооптическую структуру (1.3.9).

Основной вклад в поле дает окрестность точки так называемой стационарной фазы r=. Фаза вблизи стационарной точки квадратично зависит от расстояния до этой точки:

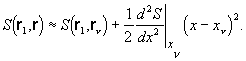(1.3.27)

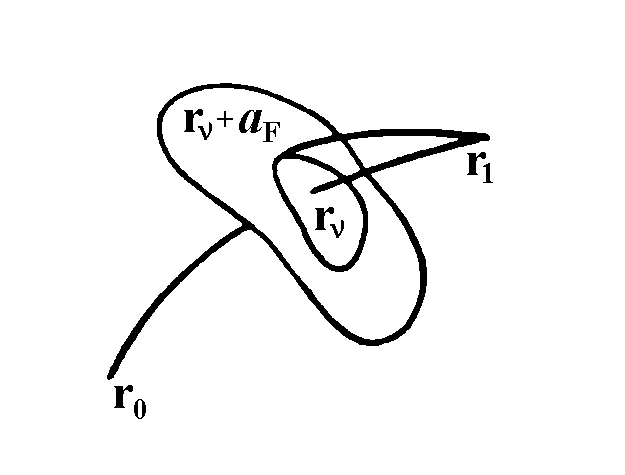
Окрестность точки стационарной фазы представляет собой ту область влияния, которая формирует поле в точке наблюдения. Область влияния, светящееся пятнышко, которое можно наблюдать, если глаз поместить в точку r₁, можно назвать первой зоной Френеля. Уточним это понятие.

Предположим, что вблизи точки стационарной фазы падающее поле имеет форму сферической волны с радиусом кривизны R. Найдем разность эйконалов вдоль луча из rn в r₁ и вдоль луча, испускаемого в ту же точку r₁ точечным источником, мысленно помещенным на волновую поверхность на краю зоны Френеля в точке . По определению, будем считать aF размером первой зоны Френеля, если эта разность эйконалов, умноженная на k, равна по модулю p :

(1.3.29)

Особенно просто определить область влияния в однородной среде. В параксиальном приближении

(1.3.30)

оставляя в (1.3.29) только квадратичные по a_F члены, получим явную формулу для радиуса первой зоны Френеля

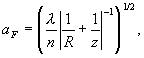(1.3.31)

где z- расстояние вдоль луча от точки стационарной фазы до точки наблюдения. Радиус кривизны волнового фронта считаем положительным (R>0) для расходящейся волны, отрицательным (R<0) для сходящейся.

Область влияния изменяется при изменении расстояния от выбранной точки наблюдения r₁ (рис. 1.3.4).

Если z® 0, то светящееся пятнышко стягивается в точку, т.е. практически передача световой энергии идет по законам геометрической оптики, которые не учитывают никаких нелокальных воздействий. Величина a_F при данном R>0 максимальна при отнесении z на бесконечность и равна при этом

(1.3.32)

Если R=¥ , т.е. фронт в районе точки стационарной фазы плоский, то размер области влияния

(1.3.33)

Если R<0, волна сходящаяся, то

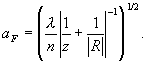(1.3.34)

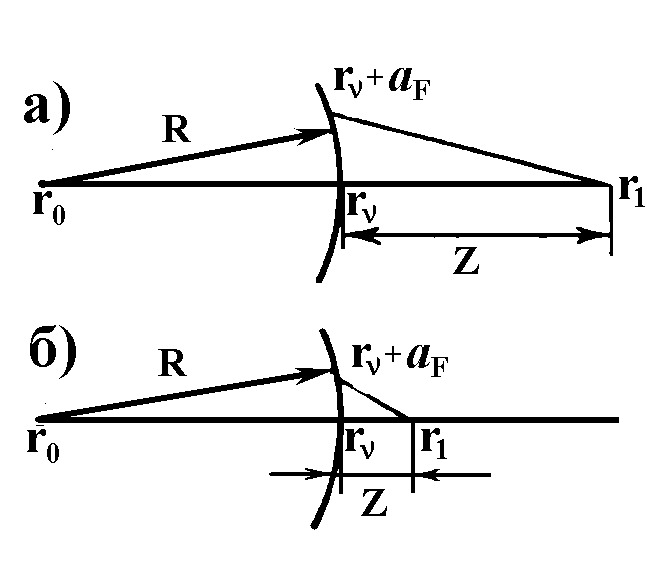
Очевидно, что на расстоянии z=|R| размер светящегося пятна растет и заполняет всю поверхность. Таким образом, на поле в фокусе влияет вся светящаяся поверхность. При размер пятна стремится к тому же пределу (1.3.32): , как и для расходящейся волны. Заметим, что лишь для плоской волны такого предела не существует- пятно растет неограниченно с увеличением z (1.3.33).

В более общем случае неоднородной среды и двух радиусов кривизны волнового фронта в выбранной на луче точке rn также существует область вокруг луча, влияющая на формирование поля в точке r₁ . Форма этой области, которая находится двумерным методом стационарной фазы, может быть довольно сложной.

Неравенство (1.3.2), при выполнении которого волну можно считать почти плоской, а среду почти однородной, является необходимым, но недостаточным условием применимости геометрической оптики. Достаточные же условия применимости должны тем или иным способом учитывать накапливающиеся погрешности, обусловленные тем, что поле нулевого приближения (1.3.3) не является точным решением волнового уравнения. Корректный учет такого рода погрешностей в общем виде представляет собой весьма трудную задачу, еще ждущую своего решения. Однако обобщая результаты многих работ, выполненных в указанном направлении, можно сформулировать некий эвристический критерий выполнимости геометрической оптики. Этот критерий требует, чтобы вблизи луча на расстоянии, много большем линейного размера первой зоны Френеля, не было резких изменений ни свойств среды, ни свойств поля. Если обозначить поперечный масштаб изменения этих свойств (точнее, наименьший из масштабов) через l^ , то условие применимости геометрической оптики запишется в виде неравенства

(1.3.35)

Это условие намного более жесткое, чем условие (1.3.2) превышения масштабов среды и поля над длиной волны. Так, если волна почти плоская, то , а этот размер в больше длины волны, и при становится как угодно большим. Растет до бесконечности область влияния и при приближении к фокусу: . Поэтому в реальной ситуации, когда нельзя обеспечить неизменные свойства среды на бесконечной поверхности, излучение плоского поля при достаточно больших z теряет лучевую структуру. В окрестности фокуса (а не только в фокальной плоскости) поле также принципиально не может быть геометрооптическим.

Область влияния для сходящихся или расходящихся лучей при приближается к конечному пределу (1.3.32), поэтому, в отличие от плоской волны, они могут быть описаны в представлениях геометрической оптики, если только выполнено условие (1.3.35).

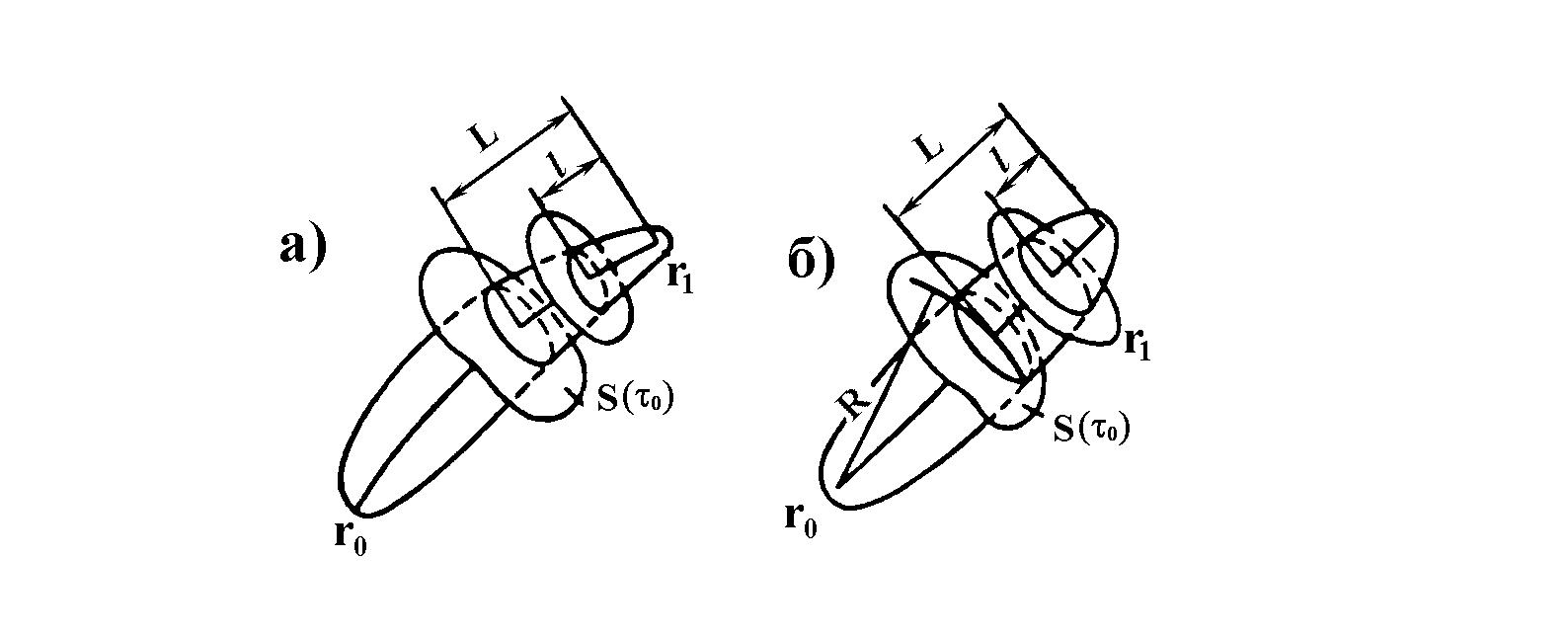
При фиксированной точке наблюдения, расположенной на луче, можно провести огибающую первых зон Френеля, выделив так называемый френелевский объем. Если, например, точка наблюдения расположена на расстоянии L от выделенной поверхности волнового фронта с радиусом кривизны R, то радиус вытянутой поверхности, ограничивающей френелевский объем,

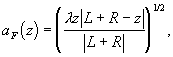(1.3.36)

где z отсчитывается от точки наблюдения вдоль луча (рис. 1.3.5). Эта формула получена из (1.3.31) очевидной заменой в ней R, т. е. радиуса кривизны на расстоянии z от точки наблюдения, на .

При анализе лучевой картины светового поля принято выделять важный структурный элемент, называемый каустикой. Каустика - это поверхность (или линия), огибающая систему лучей (рис. 1.3.6). Для плоской волны каустики нет. Каустика цилиндрической волны вырождается в фокальную линию (ось системы координат). Каустика сферической волны вырождается в точку – фокус. Каустика может сформироваться как в неоднородной среде, так и в однородной. Пример каустики в однородной среде приведен на рис. 1.3.7, где лучи – нормали к волновому фронту, который несколько отличен от сферического.

На каустике пересекаются бесконечно близкие лучи, поперечный размер лучевой трубки уменьшается до нуля, и лучевые разложения (1.3.4) поэтому не могут быть использованы, так как все коэффициенты А_i на каустике обращаются в бесконечность.

Каустика разделяет часть пространства, заполненную лучами, от каустической тени. В освещенной части через каждую точку проходит два луча – один из них уже коснулся каустики, другой еще нет. При подходе к каустике со стороны освещенной стороны наблюдается рост амплитуды поля, локальный максимум; при переходе через каустику и удалении от нее в область тени поле спадает. В направлении нормали к каустике поле в освещенной части имеет, из-за интерференции двух лучевых полей, характер стоячей волны. Вдоль каустики поле имеет характер бегущей волны.

Представление о структуре поля вблизи каустики можно получить, рассчитав распределение интенсивности в так называемом линейном слое. Пусть слева, со стороны пространства n=1, падает на плоскую границу раздела z=0 плоская волна (рис. 1.3.8). В области z>0 среда имеет линейно убывающую с ростом z диэлектрическую постоянную :

(1.3.37)

где - характеристика среды, та плоскость, на которой n=0. Предположим сначала, что плоская волна падает перпендикулярно к линейному слою. Тогда волновое уравнение для амплитуды поля

(1.3.38)

после замены переменных

(1.3.39)

принимает вид

(1.3.40)

Решение уравнения (1.3.40) пропорционально функции Эйри v(t), которая определяется интегралом

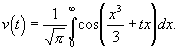(1.3.41)

Искомое поле

(1.3.42,a)

причем коэффициент пропорциональности определяется из требования непрерывности поля и его производной при t=t₀, где t₀– значение t (1.3.39) при z=0:

(1.3.42,b)

Предполагается, что амплитуда падающего поля равна единице.

Вид функции Эйри приведен на рис. 1.3.9. Значение функции вблизи нуля порядка единицы, v(0)=0.63, максимум несколько сдвинут в сторону освещенной области и достигается при t» -1: v(–1.02)=0.95.

Слева от точки z=z₀ (т.е. при t<0) эта функция при больших значениях аргумента (|t|>>1) описывает распределение поля, схожее со стоячей волной.

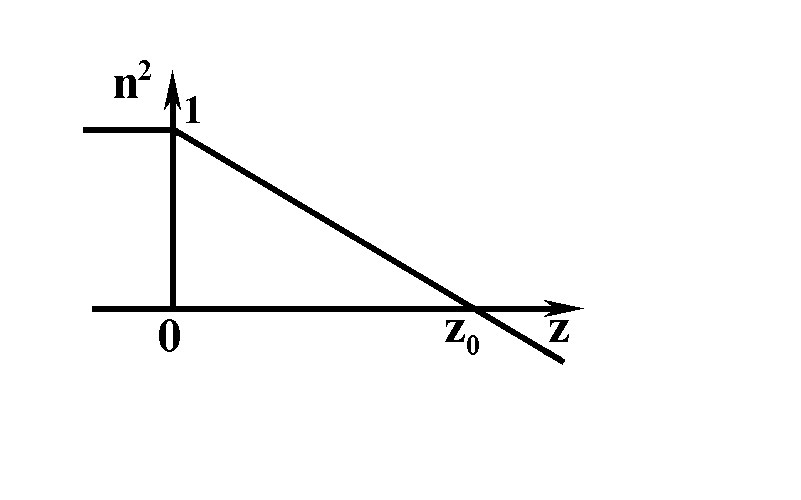
Вблизи каустики и на каустике поле не может быть описано с помощью геометрооптических лучей. На каустике – потому, что сечение лучевой трубки обращается в нуль, коэффициент расходимости (1.3.20) равен нулю, и все амплитудные коэффициенты в лучевом разложении неограниченно растут. В окрестности каустики лучевое разложение неприменимо потому, что лучи становятся неразличимыми, так как разность эйконалов двух пересекающихся лучей, один из которых коснулся каустики, а другой еще нет, меньше l /2.

Несмотря на то, что геометрооптические представления не применимы для прикаустической области, к их достоинствам следует все же отнести возможность нахождения расположения каустической области, а в некоторых случаях - и ее ширины.

Как уже указывалось, поведение лучей в световом потоке может быть определено путем использования вариационного принципа, предполагающего нахождение экстремалей функционала (1.3.14). Решение вариационной задачи оказывается более легким, если перейти к новой переменной интегрирования. Используем определение элемента длины

(1.3.43)

где

(1.3.44)

чтобы выразить (1.3.14) в виде

(1.3.45)

Здесь Р₁ и Р₂начальная и конечная точки луча.

Функция L задается соотношением

(1.3.46)

Уравнение (1.3.45) имеет точно ту же форму, что и принцип наименьшего действия Гамильтона, достаточно подробно рассматриваемого в курсах теоретической механики. Единственное отличие принципа Ферма от принципа Гамильтона заключается в том, что в принципе Ферма вместо переменной координаты t используется пространственная координата z. В классической механике функция L называется лагранжианом. Координата z обычно выбирается совпадающей с предпочтительным направлением оптической системы, известным как оптическая ось. Большинство оптических систем имеет ось симметрии, которая является также осью вращения.

Решение задачи (1.3.45) хорошо известно в вариационном исчислении и нет необходимости приводить его здесь. Оно дается уравнениями Эйлера для вариационной задачи

(1.3.47)

(1.3.48)

Подстановка выражения (1.3.46) приводит к соотношениям

(1.3.49)

(1.3.50)

Используя известную из классической механики связь между уравнениями Эйлера (1.3.47), (1.3.48) и уравнениями Гамильтона, а также соотношения (1.3.49), (1.3.50) можно формально уравнениям лучей придать вид гамильтоновых уравнений:

, (1.3.51)

, (1.3.52)

, (1.3.53)

(1.3.54)

Здесь x, y, z - cоответственно поперечные и продольная координаты точки на луче, а "импульсы" p_x и p_y задаются формулами

(1.3.55)

(1.3.56)

Из последних соотношений видно, что в параксиальном приближении значения импульсов определяют значения углов наклона лучей. Сам же гамильтониан выражается через импульсы с помощью соотношения

(1.3.57)

Представление геометрической оптики в гамильтоновой форме не просто расширяет ее аппарат, Такое представление позволяет перенести на многие геометрооптические задачи элементы анализа, применяемого к поведению динамических систем. В частности, как мы увидим в следующей главе, динамическая теория перехода детерминированных систем к хаосу позволяет вскрыть один весьма необычный механизм стохастизации излучения в регулярно- неоднородных средах.