About particularities of intensities distribution in cross-section of powerful laser beams
V.A.Gurashvilia, P.V.Korolenkob, A.P.Napartovicha, S.P.Pavlova, A.V.Rodina, N.E.Sarkarova, A.M.Zotovb
aTroitsk Institute For Innovation and Fusion Researches, Troitsk, Moscow Region, 142092, Russia
b
Moscow State University, Moscow, 119899, RussiaABSTRACT
The physical nature and manifestation of several types of instabilities and fluctuation processes in the cavity of the fast-flow CO2 –laser are considered. It was established by experiment that optimal design of optical and gas-dynamic laser sections depresses totally the high frequency fluctuations and reduces low-frequency fluctuations to the level 6-10%. It was shown that inhomogeneities in the laser cavity are apt to complicate appreciably the space-temporary structure of output laser radiation. To interpret the experimental results influence of phase aberrations on the process of formation of caustics and wavefront dislocations in laser beam is considered.
Keywords: unstable cavity, laser beam, diffraction, wavefront dislocation, caustic, power instabilities.
1. INTRODUCTION
The actual now-a-days actual problem of the improvement of the characteristics of high power technological lasers is closely connected with the investigation of the physical nature of optical inhomogeneities and instabilities in laser cavities as well as with their influence on radiation structure. High peak intensity values inherent in high power fast-flow lasers reinforce the optical inhomogeneity of the active medium, cause termodeformation of the cavity mirror and generate nonlinear self-action effects and multimode lasing in active media1,2. The important role in development of generation instability in fast-flow lasers is played self-modulation processes. They are typical for the devices with cross flow of active medium using a cavity with an unstable configuration under the condition of separate pumping and generation. The auto-oscillations of the power having the period close to time of medium crossing the cavity offer the depth of power modulation up to 100 % 3,4. Speed inhomogeneities of an active medium flow can result in stabilisation of a generation mode5. However speed inhomogeneities strengthen the phase inhomogeneities of the medium6. Aforesaid testifies that there are a lot of factors, which influence negatively on stability and quality of laser radiation. The result of this influence is usually estimated by analysis of the far-field radiation structure. At the same time much less attention is paid to the study of the light field characteristics in the near diffraction zone, the length of which for wide-aperture beams is rather significant. In this paper the spatial-temporary structure of CO2-laser beam of the near field diffraction zone is considered.
2. CHARACTERISTICS OF LASER AND EXPERIMENTAL RESULTS
As a source of radiation the technological electro
charge ÑÎ2 - laser of continuous action with flowing active medium and wavelength l =10,6m was used. The design of the laser investigated was similar to that described earlier7. Active medium in the resonator cavity was formed by replenish of ÑÎ2 gas components to a binary mix N2+He, previously exited in a discharge chamber. The flow speed of active medium varied in the range of 100-150 m/s. It was possible to change the pumping mode as well as the gas formula and optical cavity characteristics. The depth of energy-input modulation in the discharge did not exceed 5 %. The instability of gas-dynamic parameters was not more than 3 %. To pick up the energy from active medium of the laser several constructions of unstable resonators with magnification number Ì=1,12-2,2 were used. Depending on the scheme of the resonator the scope of active medium of the laser was carried out by single or double passage of radiation through the active volume. In the optical scheme of the double passage unstable resonator the angle reflectors consisting of two or three flat mirrors were used. The application of such reflectors not only allows to fill effectively the active medium with radiation, but also to level the intensity distribution in cross section of a beam by the rotation of a field in the cavity. It was possible to form radiation at the resonator output as a rectangular, square or circular with the central part shadowed by the output mirror.Measuring of power fluctuation value and the intensity distributions in the cross section of the output radiation was carried out in the previously weakened laser beam. To attenuate the high power radiation the grooved gratings made on the mirrors base, diffraction couplers on the basis of mirrors with regular sieve structure were used, as well as couplers in the form of narrow fringes of spherical mirrors ensuring the scanning of a laser beam over a small aperture of the photoreceiver. In case of insufficient value of radiation attenuation the edges of optical plates made of KCl or ZnCe were applied. Depending on the power of weakened laser beam the registration of radiation was carried out directly or by using the integrating sphere. The time of the beam aperture scanning was about 10-2 - 10-3 s. On occasion to measure the intensity distribution in the beam cross-section the small spherical mirrors with the diameter of about 5 – 10 mm were placed instead of mirror fringes. It allowed to scan the output beam aperture thus give the opportunity to register the intensity distribution with the resolution of about 3 – 7 mm in any given beam scan.
It was established that
the average value of power fluctuations does not exceed 6-10 % under the magnifying factor equal to Ì = 1,5. The varying of the magnification number in the limits Ì=1,4-2,2 did not result in appreciable changes of the character of temporal power behaviour. Under such conditions the power picked off the laser active medium decreased with increasing of Ì because of insufficient power density in the cavity. The reduction of the magnification number of the unstable resonator from Ì=1,4 up to Ì=1,12 resulted in increasing of power fluctuations. The same effect was observed when the reduction of the cavity aperture along the flow took place. However the power modulation depth in this case did not exceed 20 %. It is important, that in all experiments the generation power modulation was conducted in the low-frequency band (up to 10 Hz) and did not contain spectral components corresponding to the time of medium crossing the cavity. One can explain this effect by the fact that at the high power levels an increasing of the effective mode volume and averaging over generation area all effects, which decrease of the power stability.Contrary to the temporal behaviour of the total power the intensity in the beam cross-section was extremely unstable. Besides its transverse distribution was very complicated. The spatial modulation of intensity distribution in the beam cross-section in the near zone varied with the distance from the plane of measurement in relation to the output aperture of the resonator.
The registration of intensity distribution in cross section has shown, that in this distribution the "hot spots" with intensity much higher than its average value may randomly occur. In some cases intensity in such spots differed from average value by 5-10 times. The
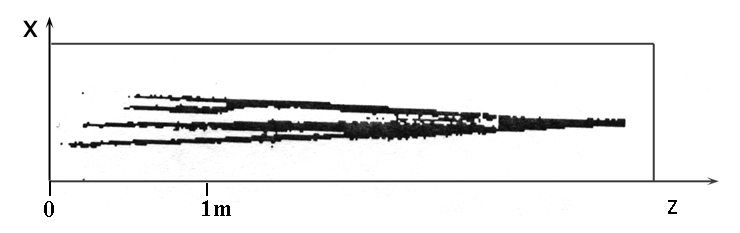
quantity of such spots in cross section of a beam varied. From one up to six such spots was registered. At registration of distribution of intensity on distance 19ì from a output aperture of laser cross size of spots varied in a range 10-20mm. They occurred by a random way in a various areas of the aperture of a beam.To improve the registration of channels with high meanings of intensity the special aerosol chamber was designed. It allowed to visualise the spatial fragments of the beam which intensity surpasses the certain level. As working medium in the aerosol chamber the fine particles of corundum weighed in air were used. To increase density of power and to achieve a threshold level of a luminescence corundum, the radiation was directed through the aerosol chamber, being previously focused with the help of a long-focal-length a mirror. Such technique allowed by character of a luminescence corundum to investigate transformations of spatial distribution of intensity in a laser beam. In fig. 1 the typical photo-picture of a luminescence of corundum particles in a converging laser beam is given. In it the channels with high meanings of intensity are precisely visible. The amount and position of such channels in process of generation are varied.
Simultaneously with registration of spatial distribution of intensity of radiation the research of features of phase distribution using the help shift interferometer was carried out. The analysis of interferograms has shown, that alongside with essential phase aberration on the wave front screw dislocations are formed. Their identification was carried out on points of branching of interference fringes. In fig. 2 interferogram of wave front with the screw dislocation is given. The registration of screw dislocation is in the consent with the earlier discovery8,9 of topological distortions of wave front in laser radiation of a rather wide class of lasers.

Fig.1. Sructure of the convergent laser beam.

Fig. 2. Transverse shift interferogfam of the laser beam. Block—screw dislocation.
Thus, investigated type of the laser at a stable level of total output power has the complex and unstable form of distribution of amplitude and phase in cross section of radiation. The mechanisms of stochastisation of a amplitude-phase structure of a beam and formation of channels with high meanings of intensity radiation can be different. One of them is connected to excitation of a superposition of transverse modes2 in a laser cavity. Another mechanism of formation of complex distribution of amplitude and phase in the near zone can be caused by the presence smooth distortion of wave front of the laser beam near output mirror.
3. DIFFRACTIONAL MECHANISM OF FORMATION OF CAUSTICS AND PHASE DISLOCATIONS IN LASER BEAMS
Let's consider in more detail the process of formation of caustics and dislocations in the field of a laser beam. The general representation about character of considered process can be received on an example about propagation of a gaussian beam, the phase of which varies in an initial plane on the harmonic law. The amplitude of a field of such wave under longitudinal coordinate z=0 is
![]() , (1)
, (1)
where m - is a parameter describing the depth of phase modulation, x,y - are cross coordinates, a -is period of modulation. At the distance z from the initial plane the field can be presented as a superposition of gaussian beams10:
![]() (2)
(2)
where Jq - is the bessel function about q order, Gq(x’,y,z’)-is a function, which describes a field of a gaussian beam11,
x’
=z sin(qa )+x cos(qa ),z’=z cos(qa )-x sin(qa ),
a =a/l .
Using for calculations of the characteristics of a field expression (2), and also the ray method used in work12, it is possible to establish the basic features of transformation of initial amplitude - phase distribution. The calculations show, that even at small depth of a phase modulation in an initial section the diffraction effects result in significant spatial redistribution of intensity. So, at meaning m = 0.1 the contrast K (K = Imax/Imin) of the picture of intensity distribution is equal to K=1.28, and at m=0.5 K=2.82. At excess of the certain critical level of modulation there are qualitative changes in wave structure. At m>1 in a field of a wave occur the beak-shaped caustics12 occur, and at m>p /2 near of caustic generatrix edge dislocations (ED), in which wave phase jump is equal to
p , begin to form.ED is located symmetrically relatively to the axes of beak-shaped caustic. Their arrangement in relation to the caustic generatrix corresponds to phase structure of a field given in work13. In this work the field is calculated on base of Persy integral. With increase of initial modulation depth of a phase the number of ED grows. The appropriate dependence is given by fig. 3. Longitudinal structure of intensity distribution is given by fig. 4 for m=1.2 and w0/a=5. From it one can see, that the phase modulation results in formation of the longitudinal channels. These channels are extended along a propagation direction of the beam and have power density much greater than its average meaning. The axes of these areas coincide with the axes of symmetry of beak-shaped caustic.
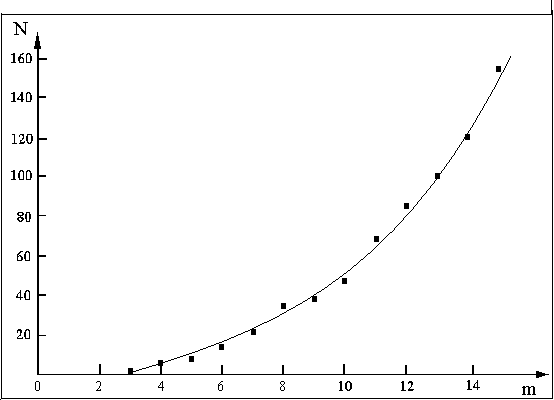
Fig.3. Dependence of edge dislocations number on the phase modulation depth. The length of the counting range – is a2/2l , width – is a.
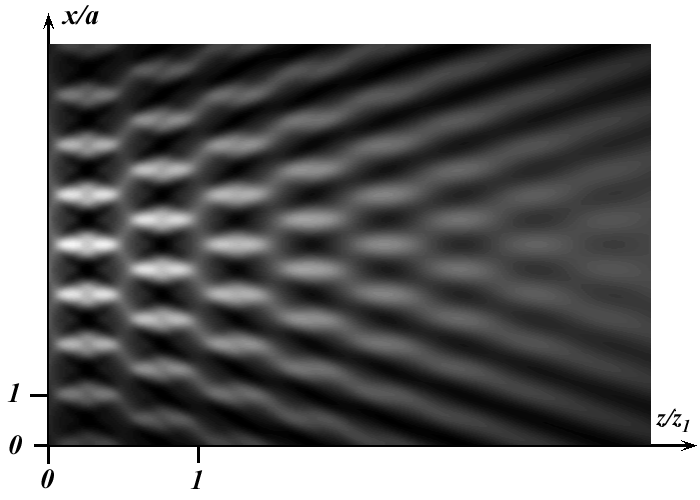
Fig. 4. Longitudinal structure of intensity of modulated gaussian beam. z1=2a2/l .
If the phase modulation in an initial plane is taking place not on one, but in two cross coordinates there is an opportunity of formation of screw dislocation2 (SD) of wave front. SD differ from ED fundamentally by topological structure (at path-tracing around SD a phase varies by 2p ). In fig.5,a the equiphase lines structure of wave front in an initial plane is given, if the distribution is as follows:
![]() (3)
(3)
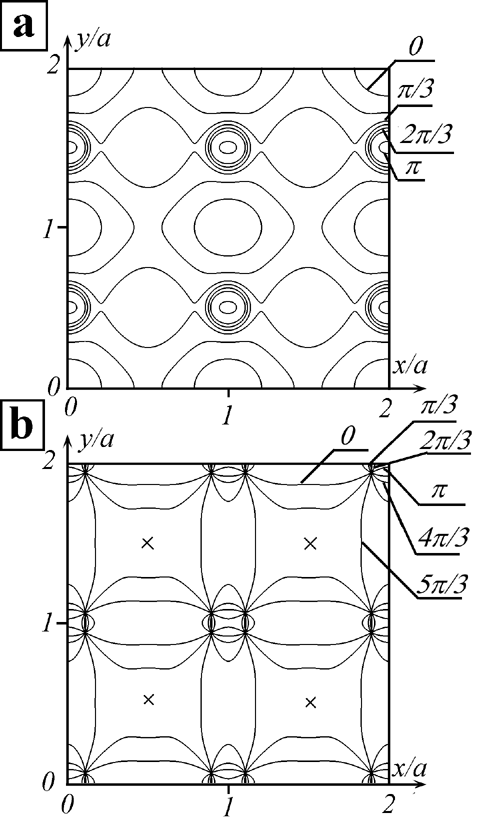
Fig.5. Structure of equiphase lines in initial (a) and z=a2/2l (b) planes, xx-caustics.
The function Ψ(
y,x) coincides with function Ψ (x,y) at replacement of cross coordinate x on cross coordinate y, C, c are constants. The structure of equiphase lines in fig.5,a is constructed for C=0.2, c =1, w0/a=5 and m=2. The position of lines testifies the presence of smooth regular distortions of wave front. In fig. 5,b the equiphase lines structure at the distances z= à2/2l are represented. SD are located in points of equiphase lines crossing.They form the original quadrupoles, each of which consists of four SD. Two of them have positive signs (are "right" ones), the other two - negative signs (are "left" ones). Quadrupoles surround the axes of caustics. As well as ED, screw dislocations arise only as the depth of initial wave front modulation exceeds certain critical meaning. If to designate through D Ô a difference between the maximal and minimal meaning of a phase in an initial plane (when modulation by one coordinate D Ô coincides with m), SD arise, when D Ô > p /2. Contrary to ED, each of which, in the strict sense, is formed in the certain plane z = Const., SD are characterised by certain longitudinal length. Fig. 6 represents the dependence of SD length changes and their longitudinal positions on parameter m in the region with width a and length a2/2l . It is clear that some dislocations have a large length compared with value a2/l , length of the other are very small.
Process of formation of wave front dislocations was investigated also by using the stochastic theoretical model. The wave with uniform amplitude and stochastic phase in one transverse coordinate in initial plane was considered. Fig 7 shows the dependence of average amount of ED n in phase correlation interval Rcor on the root mean square s of phase in initial plane. Value n was estimated in plane z=A2/2l , where A – period of largest harmonic of wave front disturbances. It is seen that n tends to unity under s tends to five. However individual dislocations are formed in laser beam even if s is equal to unity.
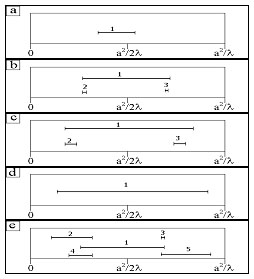
Fig. 6. Longitudinal dimensions of screw dislocations a-D f =2.0, b-D f =2.5, c-D f =3.0, d-D f =3.5, e-D f =4.0. 1,2,3,4,5-labels of dislocation.
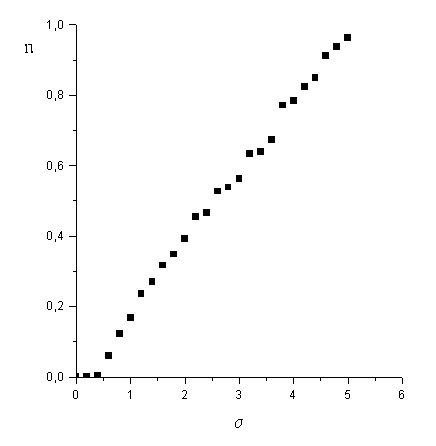
Fig. 7. The dependence of average amount of ED n in phase correlation interval Rcor on root mean square of phase s .
4. CONCLUSIONS
The results of computations specify the important role, which the smooth small-scale disturbances of wave front play in transformation of an amplitude-phase structure of radiation and formation of caustics and dislocations. The occurrence of caustics and dislocations of wave front is of threshold character and is directly connected with the depth of initial phase modulation. For practice it is important that the occurrence of the specified formations in a laser beam is connected to formation of narrow channels, in which the intensity of radiation considerably exeeds its average meaning. These results have shown agreement with experimental data concerning fast-flow CO2 laser. Thus, the problem of improvement of wave front quality in output laser beam as well as stabilisation of total power is very vital.
5. ACKNOWLEDGEMENTS
The present work was supported by the Russian Fund for Support of Leading Scientific Schools (grant N 00-15-96679) and Russian Ministry of Science (project 1.61 of the program “Physics of quantum and wave processes”).
REFERENCES
1. V.S.Golubev, F.V.Lebedev, “On stability of the radiation from fast-flow gas-discharge technological CO2-lasers. (Review article)”, Rus. J. Kvantovaya Electronica, 12(4), 663-671, (1985).
2. V. V. Valuev, A. I. Kutsenko, A. P. Naportovich, V. G. Naumov, S. P. Pavlov, N. E. "Investigation of multimode stimulated emission from powerful CO2 lasers", Rus. J. Kvantovaya Electronica, 25(3), 221-224 (1998).
3. U. A. Drejzin, A. M. Dikhne. “Self-oscillation instability of generation of fast-flow lasers based on unstable cavity”, Rus. J . Pisma JETF, 19, 818-821, (1974).
4. A. V. Artamonov, V. G. Naumov. “On Stability of the Stimulated Emission from the Fast-Flow Transverse-Priming CO2 Laser”, Rus. J. Kvantovaya Electronica, 4 (1), 178-180, (1977).
5. V. V. Lichansky, A. P. Napartovich. “On dynamic of radiation of fast-flow CO2 lasers with unstable cavity”, Rus. J . Izv. AN SSSR, Phys. Ser. 45, 399-408 (1981).
6. A. V. Artamonov, A. P. Napartovich. “Dynamic Characteristics of a Fast-Flow Electric-Discharge CO2 Laser”, Rus. J. Kvantovaya Electronica, 6(7), 1554-1556 (1979).
7. G. A. Abilsiitov, E. P. Velikhov,V. S. Golubev, F. V. Lebedev. "Perspective schemes and methods of pumping powerful CO2 technologic lasers. (Review article)”, Rus. J. Kvantovaya Electronica, 8(12), 2517-2539 (1981).
8. P. V. Korolenko, V. N. Tikhomirov. “On the structure of wave front of coupled mode systems”, Rus. J. Kvantovaya Electronica, 18(9), 1139-1141, (1991).
9. B. D. Bobrov, E. I. Dmitriev, G. Yu. Snezhkov. “Topology of phase defects of radiation of technologic CO2-lasers with stable and unstable resonators”, Rus. J. Kvantovaya Electronica, 20(7), 680-688, (1993).
10. J. W. Goodman. Introduction to Fourier Optics. Department of Electrical Engineering Standford University. Mcgraw-Hill Book Company San Francisco, New York, St. Louis, Toronto, London, Sydney 1968.
11.D. Marcuse. Light Transmission Optics. Van Nostrand Reinhold Company. New York, Cincinnaty, Toronto, London 1977.
12. U. A. Kravtsov, U. N. Orlov. Geometrical Optics of Heterogeneous Media. Moscow, Nauka, 1980.
13. L. M. Brekhovskih. Waves in Stratified Media. Moscow, AN SSSR, 1957.