Новые методы анализа экспериментальных изображений
Павел Иванов
Важной характеристикой оптического изображения является видность. При вычислении видности необходимо учитывать специфику оборудования, на котором осуществлялась съемка экспериментальных данных. Так видео камера может вносить дополнительную засветку, в большей или меньшей степени в зависимости от настройки. Так же некоторую погрешность внесет и устройство ввода отснятого фрагмента в компьютер.
Программа Tempproc ориентирована на работу с видео последовательностями, поэтому вычисление видности можно осуществлять как для отдельного кадра последовательности, так и для всех кадров последовательности целиком. Причем при вычислении видности для последовательности
возможно вычисление с усреднением по нескольким кадрам. Так же существует возможность выбора рабочей зоны вычисления видности. То есть в случае если пучок занимает малую часть экрана, то не разумно будет считать видность для всей картинки целиком, так как, скорее всего результат получиться близкий к 1, даже если картинка и не очень четкая.Как известно, видность картины выражается формулой: ![]()
Если вычисление производится традиционными методами, тогда человеку легко оценить в каком участке изображения интенсивность минимальна, а в каком наоборот максимальна. После чего интенсивность можно измерить и вычислить видность. В случае вычисления видности с помощью компьютера приходиться сравнивать интенсивности всех точек изображения и выявляя, таким образом, максимум и минимум. Но при использовании данного метода видность многих изображений получается равной единице. Это происходит вследствие того, что при вводе видео последовательности в компьютер неизбежны погрешности. Это приводит к тому, что интенсивность какой-нибудь точки в изображении будет равна нулю, что и повлечет за собой единичную видность. Для устранения подобного эффекта при вычислении видности приходиться использовать алгоритм квадратичного сглаживания. Сглаживание производиться по девяти точкам. Весовые коэффициенты получаются методом квадратичного сглаживания.
Таблица 1. Весовые коэффициенты квадратичного сглаживания
|
-1/9 |
1/9 |
-1/9 |
|
1/9 |
5/9 |
1/9 |
|
-1/9 |
1/9 |
-1/9 |
Для устранения проблем связанных с паразитной фоновой засветкой приходиться вводить константу яркости. Константа яркости - это интенсивность, полученная при съемке пустого экрана, то есть в идеале это, конечно 0. Константу яркости можно задать как вручную, так и вычислить автоматически. При вычислении константы яркости так же приходится применять алгоритм квадратичного сглаживания, дабы избежать перманентного нулевого значения.
Рис 1. Вычисление видности.
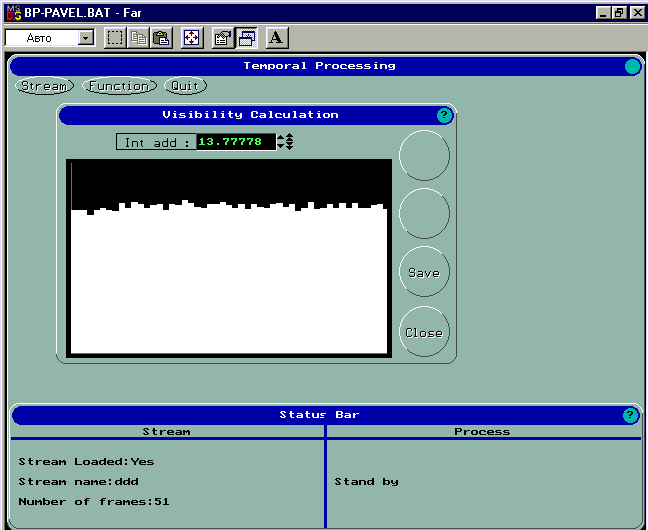
Соответственно белые столбцы (ось X) соответствуют видности (от 0 до 1), а по оси Y откладывается номер кадра в последовательности (всего 51 кадр).
В левом верхнем угле отображается константа яркости, при которой была рассчитана видность всех кадров последовательности.
Термин “вейвлет” появился сравнительно недавно – его ввели Грассман и Марле в середине 80-х годов. В настоящее время вейвлеты имеют довольно широкое применение: в системах распознавания образов, синтезаторах речи, медицине, метеорологии, а так же для архивации больших объемов данных.
Вейвлет-преобразование одномерного сигнала состоит в его разложении по базису, сконструированному из обладающей определенными свойствами солитоноподобной функции (вейвлета) посредствам масштабных изменений и переносов. Каждая из функций этого базиса характеризует как определенную пространственную (временную) частоту, так и ее локализацию в физическом пространстве (времени).
Интегральное преобразование Фурье и ряды Фурье являются основой гармонического анализа. Получаемые в результате преобразования коэффициенты Фурье поддаются достаточно простой физической интерпретации, причем простота ни в коем случае не умаляет важности последующих выводов о характере исследуемого сигнала.
Вейвлет-преобразование не так хорошо и хорошо известно, поскольку применяется сравнительно недавно, и математический аппарат находится в стадии активной разработки.
Легче всего подойти к понятиям вейвлет анализа путем аналогий с преобразованием Фурье.
Пусть
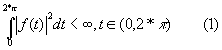
![]() Пространство квадратично интегрируемых функций с конечной энергией:
Пространство квадратично интегрируемых функций с конечной энергией:
![]()