ВЛИЯНИЕ РЕГУЛЯРНЫХ ВОЗМУЩЕНИЙ ВОЛНОВОГО ФРОНТА НА ПРЕОБРАЗОВАНИЕ СТРУКТУРЫ ЛАЗЕРНЫХ ПУЧКОВ
В.А.Гурашвили, А.М.Зотов, П.В.Короленко, Н.Э.Саркаров
Исследуется влияние регулярной модуляции фазы на динамику изменения пространственных характеристик лазерного излучения. Рассмотрены процессы и условия трансформации фазовых аберраций в топологические возмущения волнового фронта, связанные с образованием краевых и винтовых дислокаций. Обсуждается вопрос о соотношении и взаимосвязи каустических и дислокационных элементов в излучении лазера. Показано, что фазовая модуляция приводит к формированию в лазерных пучках узких каналов с повышенным значением плотности мощности.
Ключевые слова: лазерное излучение, дислокация волнового фронта, каустика.
Часто выходные пучки лазеров имеют мелкомасштабную модуляцию волнового фронта (ВФ). В газовых лазерах с движущейся активной средой такую модуляцию могут вызывать неоднородности, возникающие под действием периодической сопловой решетки [1], под влиянием страт и доменов в газовом разряде [2], в результате наложения ударных волн [3,4], а также под воздействием ряда других физических факторов. Модуляция ВФ выходных лазерных пучков чаще всего рассматривается в литературе как фактор, влияющий прежде всего на расходимость излучения. Гораздо меньшее внимание уделяется анализу метаморфоз структуры ВФ, условиям и взаимосвязи появления каустических и фазовых дислокационных образований в лазерных пучках. Такого рода образования регистрируются в излучении лазеров с самыми разными оптическими резонаторами [5, 6]. В данной работе рассмотрены процессы качественных изменений в амплитудно-фазовой структуре лазерных пучков, первоначально обладающих плавной регулярной модуляцией ВФ.
Общее представление о характере рассматриваемых процессов можно получить на примере известной задачи [7] о распространении безграничной волны, фаза которой меняется в начальной плоскости по гармоническому закону. Амплитуда такой волны имеет вид:
![]()
(1)
где m - параметр, характеризующий глубину фазовой модуляции, x - поперечная координата, а - период модуляции. На расстоянии z от начальной плоскости поле можно представить в виде суперпозиции плоских волн [7]:
![]()
(2)
где Jq - функция Бесселя порядка q, a =l /a, k- волновое число.
Это поле является частным случаем самовоспроизводящихся полей, свойства которых нашли применение в лазерной технике [8,9].
Используя для расчета характеристик поля его разложение по плоским волнам (2), а также лучевой метод, использованный в работе [10], можно установить основные особенности трансформации первоначального распределения амплитуды и фазы. Расчеты показывают, что даже при малой глубине модуляции фазы и равномерном распределении интенсивности в начальной плоскости дифракционные эффекты приводят к значительному пространственному перераспределению интенсивности. Перераспределение наиболее заметно вблизи плоскостей z=(2n+1)a2/l . Так, при значении m = 0.1 контраст К (К = Imax/Imin) картины распределения интенсивности составляет величину К=1.28, а при m=0.5 К=2.82. При превышении определенного критического уровня модуляции в структуре волны происходят качественные изменения. При m> 1 в поле волны появляются клювообразные каустики [8], а при m> p /2 вблизи образующих каустик начинают формироваться краевые дислокации (КД) волнового фронта.
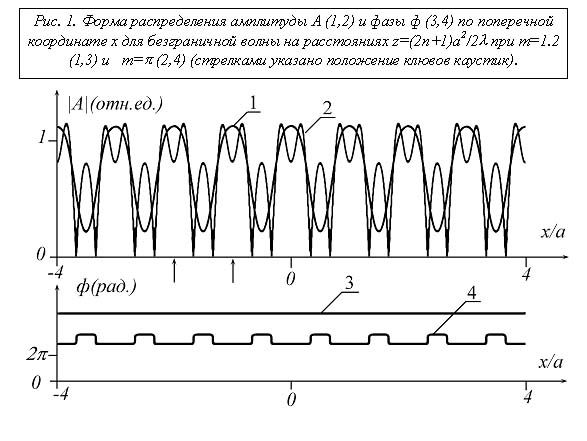
На рис. 1 приведены распределения амплитуды A и фазы Ф на расстояниях z=(2n+1)а2/2l при разных уровнях первоначальной модуляции фазы. Из хода кривых видно, что при превышении критического уровня появляются линии с нулевыми значениями амплитуды. В распределении фазы им соответствуют КД, обусловленные скачкообразным изменением фазы на величину p . КД располагаются симметрично относительно осей клювообразных каустик. Клювы каустик, располагающиеся сначала вблизи плоскостей z=(2n+1)а2/2l (n=0,1,2…) при дальнейшем увеличении глубины фазовой модуляции приближаются к плоскостям воспроизведения первоначальной структуры. При этом растет и число КД. Их расположение по отношению к образующим каустик соответствует рассчитанной на основе интеграла Перси фазовой структуре поля, приведенной в работе [11]. Продольная структура распределения интенсивности излучения приведена на рис. 2 для m=1.2. Из него видно, что фазовая модуляция приводит к формированию вытянутых вдоль направления распространения каналов, в которых плотность мощности излучения существенно превосходит ее среднее значение. Оси этих областей совпадают с осями симметрии клювообразных каустик.

Если фазовая модуляция в начальной плоскости осуществляется не по одной, а по двум поперечным координатам появляется возможность формирования винтовых дислокаций (ВД) волнового фронта. ВД отличаются от КД принципиально иной топологической структурой (при обходе вокруг ВД фаза меняется на 2p ). На рис. 3,а приведена структура эквифазных линий ВФ в начальной плоскости, если распределение поля задается формулой
![]()
(3)
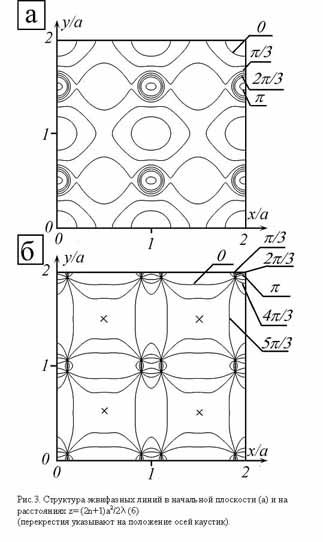
Функция Y (y,0) совпадает с функцией Y (x,0) при замене поперечной координаты x на поперечную координату y, С -константа. Структура эквифазных линий в начальной плоскости построена с помощью формулы (3) для С=0.2 и m=2. Ход линий свидетельствует о наличии плавных регулярных возмущений волнового фронта. На рис. 3,б изображена структура эквифазных линий на расстояниях z= (2n+1)а2/2l . ВД располагаются в точках пересечения эквифазных линий. Они образуют своеобразные квадруполи, каждый из которых состоит из четырех ВД. Две из них имеют положительный знак (являются “правыми”), две - отрицательный знак (являются “левыми”). Квадруполи окружают оси каустик. В отличие от КД, каждая из которых, строго говоря, формируется в определенной плоскости z = Const., ВД характеризуются определенной продольной длиной. Как и КД, дислокации винтового типа возникают лишь при превышении глубины первоначальной модуляции волнового фронта некоторого критического значения. Если обозначить через D Ф разность между максимальным и минимальным значением фазы в начальной плоскости (при модуляции по одной координате D Ф совпадает с m), то ВД будут возникать, когда D Ф > p /2.
Все вышеперечисленные эффекты были проанализированы применительно к пространственно ограниченным пучкам с гауссовым профилем распределения интенсивности. В основу расчета была положена формула (2), в которой суперпозиция плоских волн была заменена на систему распространяющихся под углом друг к другу гауссовых мод свободного пространства [12]. Горловины мод располагались в начальной плоскости.
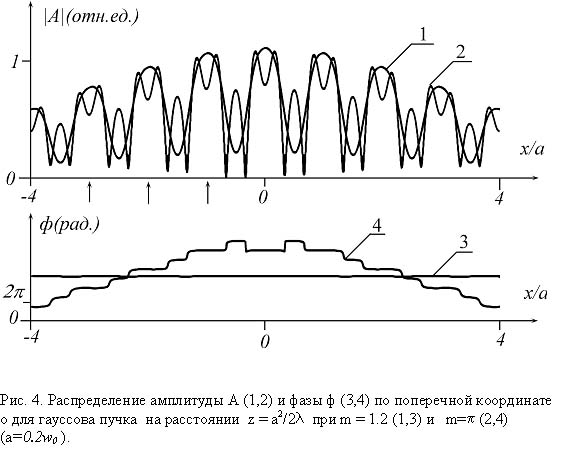
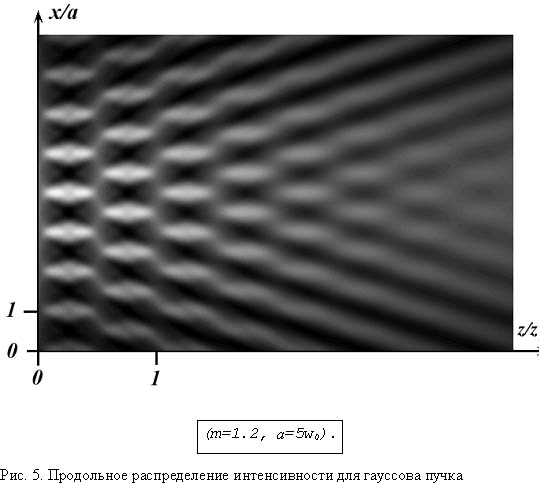
Расчеты показали, что переход к более точной модели гауссова пучка с периодической модуляцией ВФ не вносит существенных качественных изменений в данные о преобразовании амплитудно-фазового распределения по крайней мере на расстояниях, сопоставимых с характерной длиной а2/l . Как и в случае безграничной волны, дислокации ВФ начинают формироваться в ближней зоне, когда глубина модуляции фазы превосходит p /2. Сказанное иллюстрирует рис. 4, который является аналогом рис. 1 для гауссова пучка. Отношение радиуса пучка в горловине w0 к периоду модуляции а составляет w0/а=5. Из сравнения рис. 1 и 4 видно, что имеющиеся в них отличия проявляются в дифракционном “замытии” части дислокаций. Различия усиливаются с ростом координаты z по мере того, как ухудшается периодическая воспроизводимость первоначальной структуры поля. Это видно, в частности, из рис. 5, на котором изображено продольное распределение интенсивности для параметров m=1.2 и w0/а=5. Распределения, приведенные на рис. 2 и 5, близки лишь в ближней зоне. Для этой зоны характерны узкие зоны, в которой концентрируется энергия светового потока. В дальней зоне дифракции перекрытие гауссовых угловых компонент излучения ослабевает и структура излучения кардинальным образом отличается от поля безграничной волны. Излучение представляет собой “веер” пучков, интенсивность которых убывает с увеличением угла наклона.
Фазовая модуляция гауссова пучка по двум поперечным координатам, если ее глубина превосходит указанный выше критический уровень, приводит к появлению на волновом фронте ВД. Как и в безграничной волне они обладают определенной продольной длиной, увеличивающейся с ростом глубины модуляции. Это свойство ВД значительно облегчает их экспериментальное обнаружение. В дальней зоне дифракции изменения фазы в начальной плоскости по двум координатам будут вызывать формирование двух вееров пучков, располагающихся во взаимно перпендикулярных плоскостях.
Заметим в заключение, что результаты выполненного анализа могут быть частично перенесены и на случай нерегулярной плавной модуляции ВФ, если длина рассматриваемой пространственной области сопоставима с величиной ан2/l , где ан - характерный размер нерегулярных возмущений ВФ. В частности, это относится к факту образования в световом поле каналов с повышенным значением плотности мощности и появлению дислокаций волнового фронта при превышении фазовыми возмущениями определенной величины.
Таким образом, результаты расчетов указывают на важную роль, которую играют плавные возмущения ВФ в трансформации амплитудно-фазового профиля излучения и формировании каустических и дислокационных образований. Появление каустик и дислокаций волнового фронта носит пороговый характер и непосредственно связанно с глубиной первоначальной модуляции фазы. Для практики важным является то, что появление указанных образований в лазерном пучке сопряжено с формированием узких каналов, в которых интенсивность излучения значительно превосходит ее среднее значение.
Работа выполнена при финансовой поддержке государственной научно-технической программы “Физика квантовых и волновых процессов” (проект 1.61) и физического учебно-научного центра “Фундаментальная оптика и спектроскопия”
ЛИТЕРАТУРА