УДК 621.373.826
А.Ю.Лоскутов, А.В.Мушенков, А.И.Одинцов, А.И.Федосеев.
НЕСТАЦИОНАРНЫЕ И ХАОТИЧЕСКИЕ РЕЖИМЫ ГЕНЕРАЦИИ В ЛАЗЕРНЫХ СИСТЕМАХ С ПОПЕРЕЧНОЙ ПРОКАЧКОЙ
Аннотация:
На основе модельных расчетов исследована динамика генерации быстропроточного газового лазера со стационарной неоднородной накачкой внутри неустойчивого резонатора. В зависимости от профиля накачки и параметров системы наблюдались различные динамические режимы генерации. Детально исследованы свойства хаотической генерации и сценарий ее развития. Обсуждается возможность управления временными характеристиками лазера путем изменения профиля накачки.
НИИ Ядерной Физики МГУ, 1999
A.Yu.Loskutov, A.V. Mushenkov, A.I.Odintsov, A.I.Fedoseev.
E-mail mushenkov@yandex.ru
Preprint of NPI MSU
NON-STATIONARY AND CHAOTIC OPERATION OF THE FAST CROSS-FLOW LASER SYSTEMS.
Abstract
The dynamics of the lasing of the fast crossflow gas laser with the inhomogeneous steady state pumping in the unstable resonator by means of numerical modeling is investigated. Depending on the system parameters the various dynamical regimes of operation are observed. The detailed investigations of the chaotic lasing features as well as the chaos onset are performed. The possibilities of the control of the laser output characteristics are discussed
Введение
Светодинамические явления в лазерах, такие как оптическая неустойчивость, автопульсации излучения, хаотическая генерация представляют большой интерес с точки зрения общей проблемы нелинейной динамики распределенных систем [1-3]. Практическое использование этих явлений связано с разработкой на их основе принципиально новых методов управления временными характеристиками лазеров [4,5]. В лазерах с движущейся активной средой, к числу которых принадлежит большинство типов современных технологических лазеров, существуют специфические механизмы неустойчивости стационарной генерации, обусловленные нелокальным характером взаимодействия поля со средой и возникновением обратной связи между различными пространственными зонами системы [6,7]. При этом динамика генерации в сильной степени определяется пространственными градиентами параметров системы в направлении потока среды [7,8]. В работе [8] было показано, что в быстропроточном лазере (БПЛ) с неоднородной накачкой внутри неустойчивого резонатора (НР) при соответствующем выборе профиля накачки и других управляющих параметров системы, могут наблюдаться различные динамические режимы генерации, включая разные виды периодической автомодулированной генерации и хаотическую генерацию. В настоящем сообщении приводятся результаты расчетов временных и энергетических характеристик такого лазера. Значительное внимание уделено свойствам хаотической генерации и сценарию ее развития, которые ранее в подобных системах не исследовались.
Расчетная модель
Расчёты проводились в рамках модели, описанной ранее в [8]. Рассматривался неустойчивый резонатор с одинаковыми зеркалами цилиндрической геометрии. Поле в резонаторе описывалось в приближении геометрической оптики. Принималось, что потери на зеркалах и в среде отсутствуют, а потери q = lnM/2L, связанные с расширением пучка, равномерно распределены по длине резонатора L (М - коэффициент увеличения на двойной проход). Как известно, если величина М не велика (М Ј 2), то можно пренебречь изменением поля по длине резонатора и ограничиться решением одномерной задачи. Кроме того, в БПЛ время затухания поля в резонаторе t r=(cq )-1 обычно намного меньше характерных времен релаксации населенностей уровней и времени пролета газа через оптический канал t f = h/u ( h - апертура резонатора, u - скорость потока). Поэтому для расчёта интенсивности излучения допустимо использовать уравнение квазистационарной генерации
![]() , (1)
, (1)
где
I(x,t)-интенсивность поля, a (x ,t) - коэффициент усиления среды и координата x отсчитывается от оси резонатора навстречу потоку.Активная среда описывалась простейшим модельным уравнением для коэффициента усиления с одной релаксационной константой
![]() , (2)
, (2)
где
s - сечение оптического перехода, t - время релаксации инверсии, S - скорость накачки.В большинстве расчётов профиль накачки задавался в виде
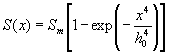 , (3)
, (3)
где
h0 - ширина зоны неоднородности накачки вблизи оси НР (h0<< h), Sm - максимальная скорость накачки вдали от оси (x>>h0). При данном выборе S(x) обеспечивается быстрый спад скорости накачки до нуля при приближении к оси резонатора. Величина Sm определяет максимальный коэффициент усиления a m= s Smt , который достигается в неподвижной среде в отсутствие генерации. Система полностью описывается заданием независимых параметров t /t f, h/h0 , q /a m и параметра a in/a m , характеризующего значение коэффициента усиления a in на входе в резонатор. Расчеты были выполнены для трех значений h/h0=0,05, 0,1 и 0,2. При этом, как правило, принималось a in=a m. Другие два параметра варьировались в широких пределах. При описании динамического поведения системы в качестве основного управляющего параметра использовалось отношение t /t f.
Регулярные режимы генерации
Численные расчеты нестационарных профилей интенсивности I(x,t) и коэффициента усиления a (x,t) в зависимости от параметров системы позволяют установить области существования различных динамических режимов генерации. На рис.1 эти области показаны в координатах (t /t f., q /a m) для значений h/h0=0,1, a in/a m=1. Сплошная кривая показывает границу устойчивости стационарной генерации (область I). В областях II и IV наблюдаются режимы автомодулированной импульсно-периодической генерации, в области III - хаотическая генерация. Штрих-пунктирная кривая дает пороговую величину потерь резонатора, выше которой генерация невозможна.
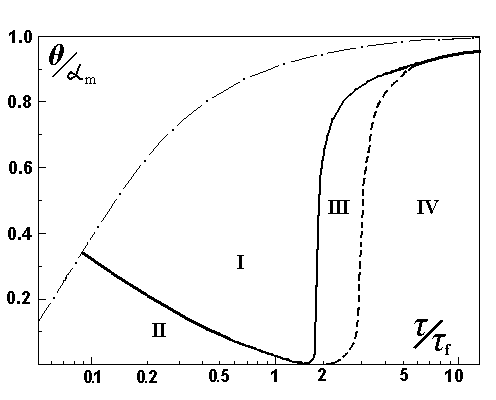
Рис. 1. Области существования различных динамических режимов генерации
Типичные временные зависимости выходной мощности автомодулированной генерации приведены на рис.2. Данные этого и последующих рисунков соответствуют относительной величине потерь резонатора
q /a m=0,26. В области II (t /t f<1) наблюдаются импульсы с относительно высокой частотой повторения с периодом T<<t f (рис. 2a). Как показали дополнительные расчеты, их ширина и форма зависят от детального вида профиля накачки. В области IV период следования импульсов оказывается близок к времени пролета T» t f. Вблизи границы хаотической генерации импульсы имеют сложную форму (рис.2b). В Фурье-спектре интенсивности G(n ), приведенном для этого случая на рис 2d, структура импульсов отражается в модуляции огибающей спектральных компонент. При дальнейшем увеличении параметра t /t f импульсы приобретают простую форму (рис.2c). Отметим, что в области t /t f>>1 ширина и форма импульсов не могут быть корректно рассчитаны в рамках использованной нами модели. Численные расчеты обнаруживают эффект неограниченного обострения импульсов, сопровождающегося ростом их пиковой интенсивности. В реальных системах достижимое сужение импульсов ограничивается как инерционностью резонатора, так и отсутствием резкого спада интенсивности на краю апертуры зеркал резонатора вследствие дифракции излучения (на рис. 2с ширина импульсов обусловлена шириной специально вводимого в расчет сглаженного края зеркала).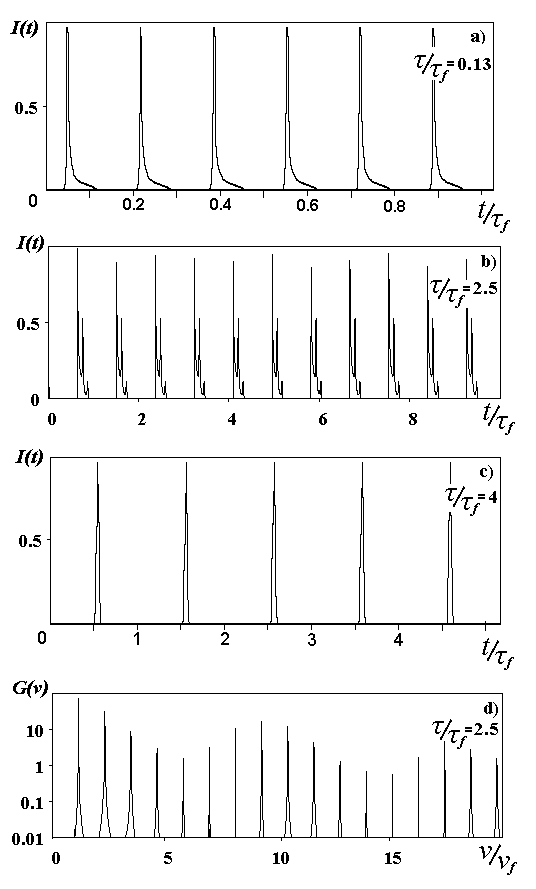
Рис. 2. Временные зависимости мощности автомодулированной генерации для различных значений параметра
t /t f (а-с) и Фурье-спектр для t /t f =2,5 (d)Наличие двух областей автомодулированной генерации с различными частотами повторения импульсов указывает на существование двух механизмов автомодуляции. Первый из них имеет место при
t >>t f (область IV на рис.1), когда восстановление инверсии обусловлено сменой газа в резонаторе. Масштаб пространственной неоднородности поля и коэффициента усиления в этом случае определяется апертурой резонатора h, период следования импульсов T близок к t f. Второй механизм автомодуляции, действующий в области II при t <<t f, связан с восстановлением инверсии под действием внутренней накачки и переносом и переносом возбужденных молекул к оси резонатора. Период следования импульсов при этом определяется как временем релаксации t , так и временем пролета молекул через зону неоднородности накачки t 0= h0/u , тогда как условия на входе в резонатор и полное время пролета t f не оказывают влияния на динамику генерации.
Хаотическая генерация
При исследовании хаотической генерации наряду с временными зависимостями интенсивности и Фурье-спектрами использовались также построение отображений Пуанкаре и определение размерностей хаотических аттракторов. Впервые для такого типа систем подробно исследовался сценарий рождения хаоса и его эволюции при изменении управляющего параметра.
При построении отображений Пуанкаре, как правило, фиксировалось значение выходной мощности Iout=x0=const, а в качестве динамических переменных x1 и x2 выбирались значения интенсивности на оси резонатора и величина коэффициента усиления в средней точке апертуры резонатора. На рис.3 показана эволюция отображений Пуанкаре при развитии хаоса из стационарной генерации с увеличением управляющего параметра. Потеря устойчивости стационарной генерации наступает при увеличении параметра до значения t /t f =1,690. При этом наблюдается слабая модуляция (с глубиной ~ 0,3 %) интенсивности генерации периодическим сигналом с частотой n m=7.28n f, где n f=1/t f - пролетная частота. Картина в сечении Пуанкаре соответствует простому предельному циклу с наложением шумовых искажений.
При дальнейшем увеличении параметра до значения t /t f =1,693 происходит следующая бифуркация, которая соответствует рождению из предельного цикла двумерного тора с плотной обмоткой (рис.3а). Это отвечает возникновению квазипериодической динамики с двумя несоизмеримыми частотами n 1 и n 2. Разность частот близка к пролетной частоте W = n 2 -n 1 @ n f. Картина генерации имеет вид биения двух частот с глубокой модуляцией интенсивности.
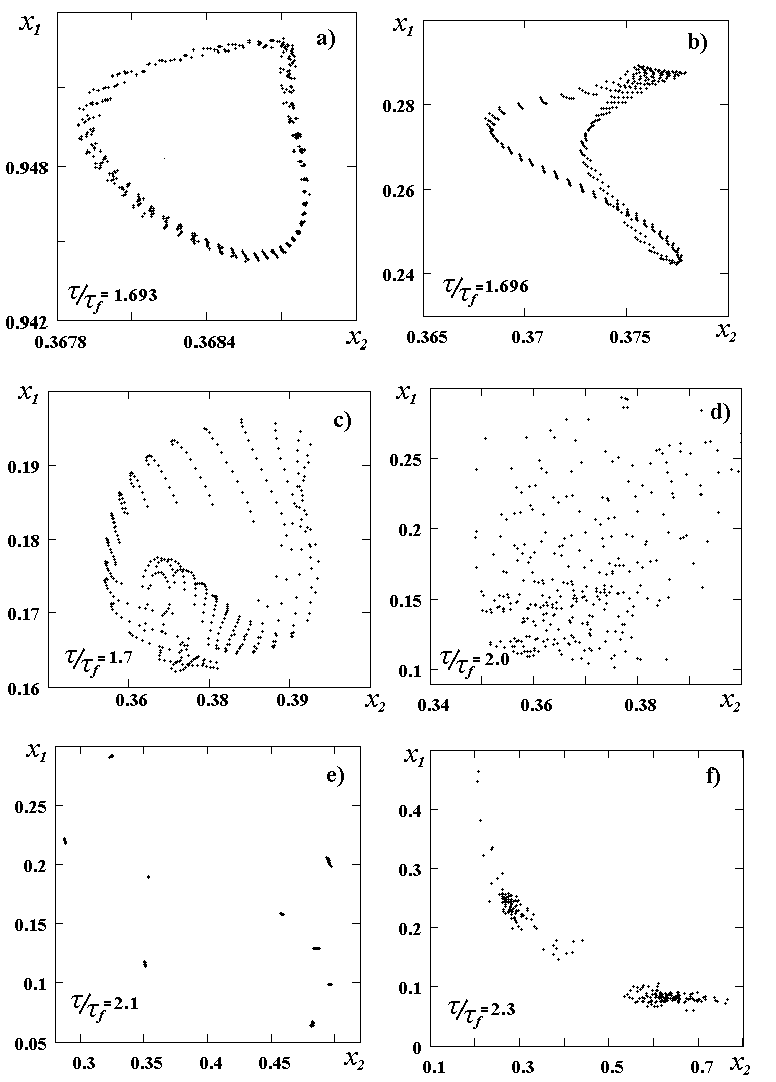
Рис. 3. Вид отображений Пуанкаре для различных значений управляющего параметра
Начиная со значения
t /t f =1,696 картина отображения Пуанкаре принимает характерный вид, показывающий, что поверхность тора приобретает сложную форму и становится негладкой (рис. 3 b,с). В соответствии со сценарием Гаврилова-Шильникова на этой стадии тор начинает гофрироваться [9]. Это иллюстрирует рис.4, на котором изображена проекция аттрактора на плоскость x0=const. В спектре этот процесс проявляется уширением основных гармоник и появлением более высоких гармоник и составных частот. При этом вид генерации эволюционирует от простых биений к достаточно сложному динамическому режиму.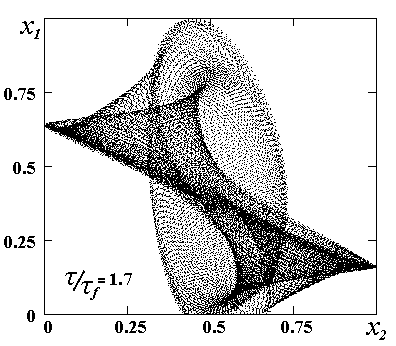
Рис. 4. Проекция аттрактора на плоскость x
0=constРазрушение тора и переход от квазипериодической динамики к хаотическим колебаниям занимает некоторый диапазон значений
t /t f и завершается при t /t f =1,71. При дальнейшем увеличении значения управляющего параметра временная структура генерации становится все более нерегулярной, наблюдается дальнейшее усложнение спектра и уширение спектральных компонент. В сечениях Пуанкаре появляется множество неупорядоченно расположенных точек. Таким образом, в пределах области своего существования хаос обладает различной степенью "глубины". В качестве примера "глубокого" хаоса на рис.3d и 5а приведены характеристики генерации при t /t f =2. В то же время на краях своей области существования структура хаотических колебаний значительно упрощается. Для значения t /t f =2,3, при наличии достаточно сложного вида спектра и временной структуры излучения (рис.5c), в сечении Пуанкаре точки группируются как бы в отдельные пятна (рис.3f). В дальнейшем при значении t /t f =2,4 хаотическая генерация вырождается в квазипериодический режим, а при t /t f =2,5 в строго периодический режим. Интересно отметить, что упрощение отображения Пуанкаре, которое может свидетельствовать о переходе системы к регулярной динамике, наблюдается также вблизи середины диапазона хаотической генерации в области значений t /t f ~ 2,1-2,2 (рис.3e). Временная картина генерации выглядит периодической с периодом Т» 3,3t f, хотя и характеризуется чрезвычайно сложной структурой импульсов. Анализ Фурье-спектра (рис.5b) показывает, что в этом случае частоты n 1 и n 2 в пределах ошибки определения оказываются соизмеримыми (7n 1=4n 2) и, по-видимому, происходит захват частот гармоник.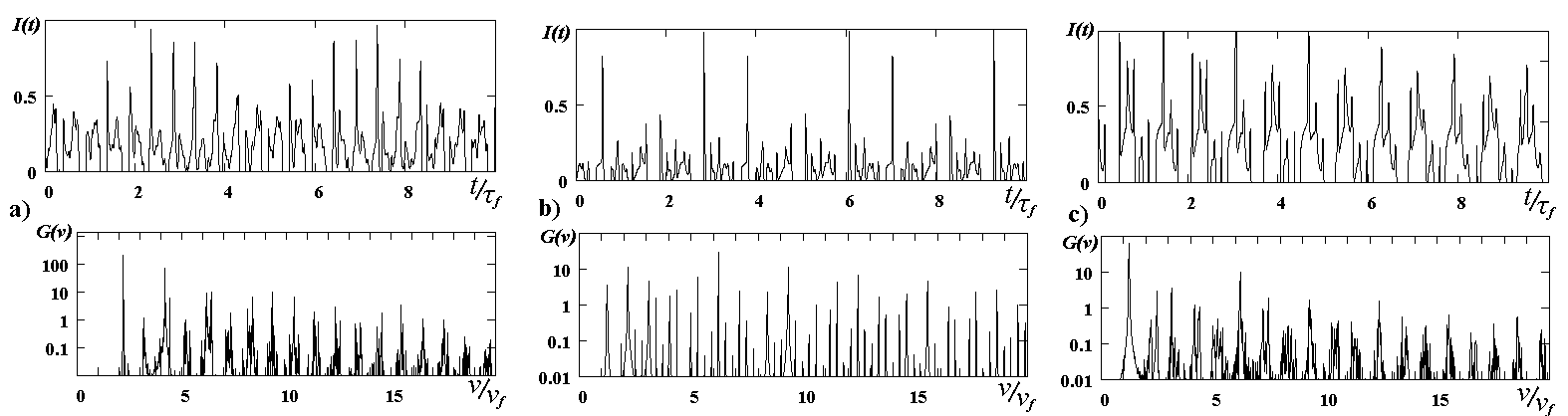
Рис. 5. Временные зависимости мощности генерации (вверху) и Фурье-спектр (внизу) для значений управляющего параметра
t /t f =2,0 (а), 2,1 (в) и 2,3 (с)Количественной характеристикой меры неупорядоченности системы помимо спектра показателей Ляпунова может служить размерность вложения хаотического аттрактора [2]. Для данной распределенной системы, описываемой уравнениями в частных производных, определение размерности вложения имеет особое значение, так как ее знание позволяет найти число эффективных степеней свободы. В свою очередь это позволяет при некоторых
дополнительных предположениях описать исходную систему набором обыкновенных дифференциальных уравнений [2]. В качестве другой количественной характеристики хаотической генерации определялась корреляционная размерность аттрактора. В расчетах был использован известный метод, предложенный П.Грассбергером и И.Прокаччиа (см.[2]), который позволяет определить обе указанные размерности. На границах исследуемой области при значениях t /t f =1,69 и 2,5, где динамика системы описывается предельным циклом, найденная размерность вложения минимальна и составляет de=4 и 5, соответственно. В областях квазипериодической генерации (t /t f =1,7 и 2,4) она увеличивается. В области хаоса размерность вложения еще более возрастает и максимальная ее величина de=8 достигается в диапазоне t /t f =1,8 - 2, соответствующем наиболее "глубокому" хаосу. Таким образом, возникновение хаотической генерации связано с усложнением динамической системы, описывающей лазер, и увеличением числа ее эффективных степеней свободы. В диапазоне t /t f =2,1 - 2,2, где частоты n 1 и n 2 соизмеримы, наблюдается локальное уменьшение величины de. Полученные данные показывают, что адекватное описание исследуемой распределенной системы проточного лазера может быть получено в модели, использующей систему из небольшого числа обыкновенных дифференциальных уравнений.Характер изменения корреляционной размерности аттрактора в зависимости от
t показывает, что по сравнению с квазипериодическим режимом (t /t f =1,7 и 2,4) корреляционная размерность хаотического аттрактора увеличивается и в области глубокого хаоса приближается к значению dc =3. Изменение размерности свидетельствует о том, что имеет место перестройка хаотического аттрактора.
Заключительные замечания
Как показывают расчеты, энергетическая эффективность рассматриваемой системы может быть достаточно высока, поскольку неоднородность накачки при малом размере зоны неоднородности (h0<<h) не приводит к заметному ее снижению. Эффективность съема энергии с активной среды в режимах автомодулированной и хаотической генерации превосходит величину h ~ 0,6. Подобные системы могут представлять практический интерес. В частности, на их основе может решаться задача создания универсального технологического лазера с переключением режимов генерации. Необходимое изменение профиля накачки может быть наиболее удобно осуществлено в варианте электроразрядного лазера с секционированными электродами. Отметим также, что выполненные расчеты имели целью выявление наиболее общих качественных закономерностей динамического поведения данного типа систем и по нобходимости носят модельный характер. Для реальных систем, таких как СО2 и СО БПЛ, естественно, потребуется конкретизация кинетической модели активной среды.
Работа выполнена при поддержке Миннауки РФ по программе "Физика лазеров" (пр. № 1.60)
Литература