Light-dynamic phenomena in fast-flow lasers (FFL) such as the optical instabilities, self-oscillations, chaotic lasing are of the great interest from the general point of view [1-3]. Practical applications of these phenomena are based on the fact that they can be used for the elaboration of new methods for the laser output temporal characteristic control [4,5]. The lasers, which use the motion of the active medium (note that the majority of the modern technological lasers are of the similar type) demonstrate the specific mechanisms of the continuous lasing instability. The mechanisms are caused by the non-local mode of the medium and field interaction and by the origination of the flow created feedback between the various spatial parts of the cavity [6,7]. In the case the dynamics of lasing is defined in a high degree by the spatial gradients of the system parameters in the flow direction [7,8]. As pointed out in Ref. [8], the suitable choice of the spatial pumping profile may cause the various operating regimes of the laser with fast crossflow of the active medium through an unstable cavity. Not only cw lasing, but also various self-pulsing regimes and chaotic lasing were observed.

The results of calculations of temporal and energy characteristics of the laser are presented in our report. The main attention is paid on the chaotic lasing features and chaos onset. The detailed investigations of the mentioned problems for the similar types of laser systems were performed for the first time.

Our calculations were carried out in the frameworks of the model given in Ref. [8]. The cylindrical unstable cavity supplied with the same mirrors was considered. The geometric-optics approximation was adopted for the description of the field in the cavity. We assumed that the losses in the active medium and in the mirrors, and the losses q = lnM/2L, associated with the beam broadening in the cavity are distributed uniformly over the cavity length L (M is the total round-trip magnification). As known, if the magnitude of M is not too large (М £ 2) the model can be simplified by ignoring the variation of the field along the cavity length. By this reason a one-dimensional distributions of the intensity I(x,t) and the gain a (x,t) along a transverse coordinate can be considered. Since the decay time t _r=(cq )^-1 of the cavity field in a FFL is usually much shorter then the characteristic relaxation times of the level populations and the time taken by gas to travel across the optical channel t _f = h/u ( h is the cavity aperture and u is the flow velocity), quasi-cw lasing equation for the intensity can be appropriated:

where the coordinate x is measured from the cavity axis opposite to the direction of the flow. We described the active medium by the simplest equation for the gain with one relaxation constant

, (2)

where s is the cross section of an optical transition; t is the inversion relaxation time; S is the pumping rate. In the majority of our calculations the spatial pumping profile was assumed to be

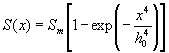, (3)

where h₀ is the pumping inhomogeneity zone near the cavity axis (h₀<< h), S_m is the maximum pumping rate far from the axis (x>>h₀). When S(x) is described in this way, there is the steep fall of the excitation rate near the optical axis of the cavity. The value of S_m determines the maximum gain a _{m= s} S_mt achieved in a medium at rest in the absence of lasing. The investigated laser system is described completely by specifying four independent parameters t /t _f, h/h₀, q /a _m and a _in/a _m (a _in=a (h,t) is the gain in the cavity input). The calculations were performed for three values of h/h₀ (h/h₀ =0,05, 0,1 and 0,2) and the input game was assumed to be a _in=a _m. Two another parameters were varied in our numerical calculations. The ratio t /t _f was used as the main governing parameter for the description of the dynamic behavior of the system.

Numerical simulations of the lasing dynamics of the system described above yielded transient profiles of the field intensity I(x,t) and the gain a (x,t), corresponding to different parameters of the system. An analysis of these profiles enabled us to identify four main regions with different values of parameters each, of them characterized by a specific dynamic behavior of the system. These regions are plotted in Fig.1 in terms of the coordinates (t /t _f, q /a _m ) for the rations h/h₀=0,1, a _in/a _m=1.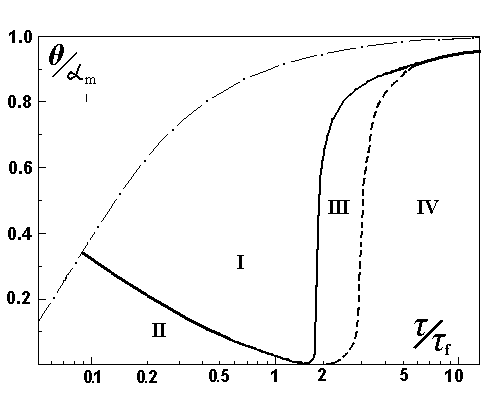

The continuous curve shows the boundaries of the cw lasing (region I) The regular self-pulsations occur in regions II and IV. The chaotic lasing was observed in region III. The dashed curve represents the threshold cavity losses q above which lasing is impossible.

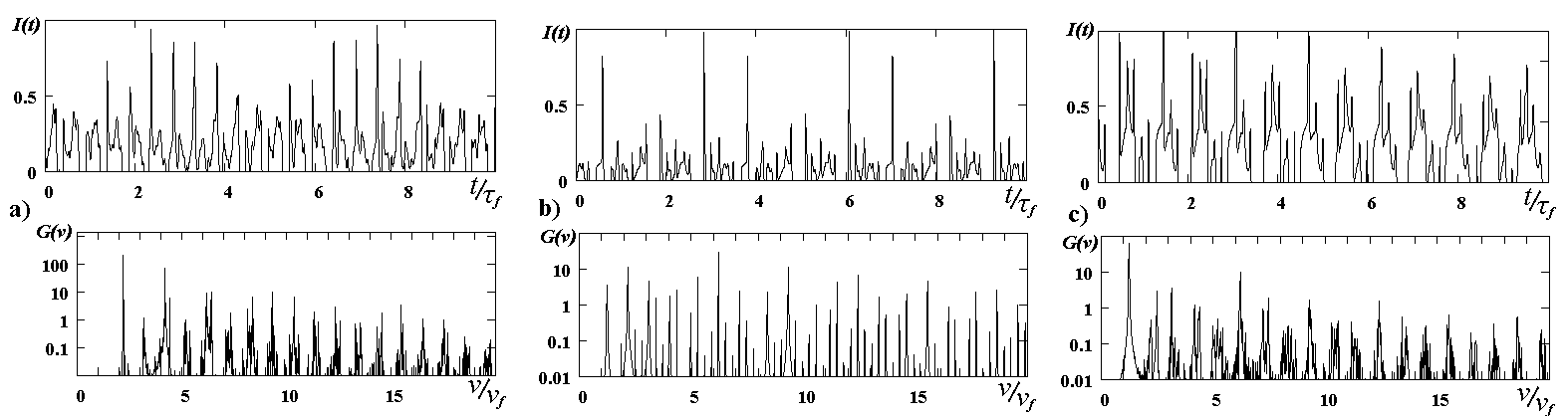
Fig.2 shows typical time dependencies of the self-pulsing oscillations intensity I(h,t) at the cavity output (the data presented in Fig.2 as well as in following figures were obtained for the relative losses of the cavity q /a _m=0,26).

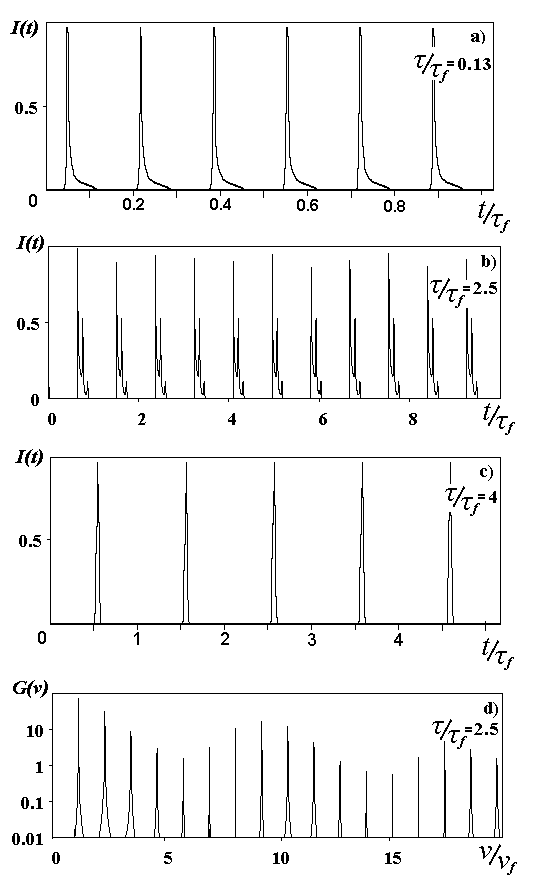
In the region II (t /t _f<1) there are regular self-pulsations with a relatively high pulse repetition frequency (period T<<t _f) (Fig.2a). The additional calculations showed the dependence of the width and the shape of the pulses on the accurate pumping profile. Region IV corresponds to generation of short pulses with the repetition period close to the flow time T» t _f. Shapes of the pulses was found complex near the boundaries of the chaotic lasing (Fig.2b). The Fourier spectrum G(n ) of the intensity is shown here (Fig.2d) for the case. The structure of the pulses associates with the envelope of the set of spectral components. Further increase of t /t _f is accompanied by the simplification of the pulse shapes (Fig.2c). Note, that the width and the shape of pulses cannot be found correctly in the framework of our model in the region where t /t _f>>1. The calculations demonstrate the effective peaking of pulses as well as non-limited growth of the pulse peak intensities. The really achieved compression of pulses is limited by two different factors. One is the decay time of the cavity field t _r and the other is the absence of the abrupt fall of the intensity profile at the edge of the mirror aperture (the smooth decrease of the intensity is due to the difraction of the radiation). The width of the pulses presented in Fig.2c was determined by the width of the artificially curved edges of cavity mirrors.

The existence of two regions of self-modulated lasing with different pulsation frequencies identifies two different self-modulation mechanisms. The first occurs in region IV (Fig.1) for t >>t _f. The inversion recovery is the result of replacement of the active medium in the cavity. The scale of the spatial inhomogeneity of the field intensity and the gain is in this case governed by the cavity aperture h and the self-pulsation period T is close to the flow time t _f. The second self-modulation mechanism corresponds to t <<t _f, in region II (Fig.1). Here, the inversion recovery in the axial zone occurs due to the pumping in the neighboring zones and motion of the excited molecules towards the cavity axis. The pulse repetition period is governed by the relaxation time t and by the time taken to cross the inhomogeneity zone t ₀= h₀/u . At the same time the conditions at the entry of the gas into the cavity and flow time t _f do not affect the lasing dynamics in this case.

Along with study of time dependencies of the intensity and Fourier spectra we use Poincare maps constructing and the determining of the attractor dimensions to point out the features of the chaotic lasing. The detailed study of the chaos onset and its evolution by the change of the governing parameter were performed.

When Poincare maps were constructed the value of the output intensity was assumed constant I_out=x₀=const as a rule. The intensity at the cavity axis and the gain in the mean point of the cavity aperture were taken as the dynamical variables x₁ and x₂. Fig.3 illustrates the evolution of Poincare maps of the developing chaos. It is originating from the stable cw lasing as the governing parameter is being increased. The loss of the cw lasing stability is taken place when the value of the governing parameter is increased to t /t _f =1,690. The weak periodic intensity modulation (about 0.3% deep) at the frequency n _m=7.28n _f (where n _f=1/t _f is the transit frequency) can be observed in the case. The image of the Poincare map corresponds to the ordinary limit cycle accompanied with the noise distortions.

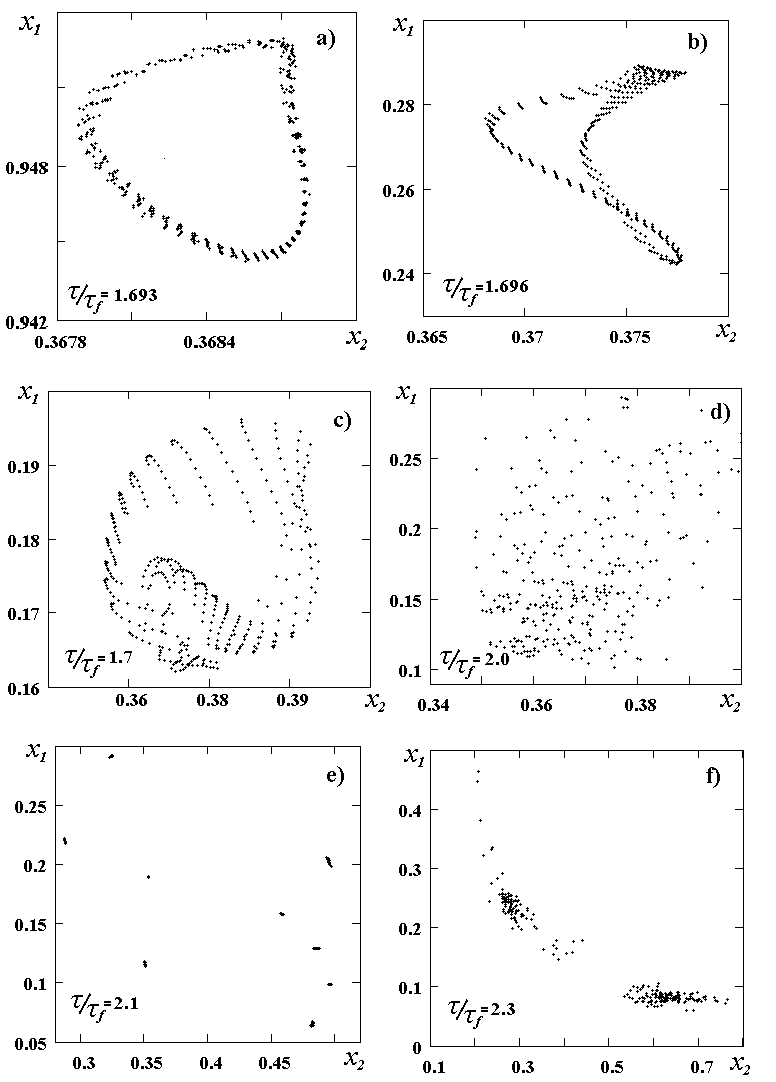
Further increase of the parameter to the value t /t _f =1,693 leads to next bifurcation which corresponds to the transformation of the limit cycle into the torus with the close winding (Fig.3a). The fact indicates quasi-periodical dynamic of the system at this step. Fourier spectrum of the intensity shows two incommensurable frequencies n ₁ and n ₂. The difference of the frequencies is close to the transit frequency W =n ₂ -n _{1 @} n _f. Corresponding time dependence of the laser radiation intensity looks as the deeply modulated beatings.

While the parameter t /t _f increases beginning from t /t _f =1,696 the characteristic view of the Poincare maps makes clear that the torus significantly deforms into a more complex shape. The feature of the deformation is that the torus gets non-smooth surface (Fig.3b,c). It can be illustrated by the constructing the projection of the attractor on the x₀=const plane (Fig.4).

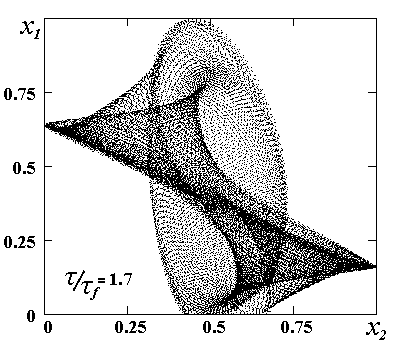
This fact is known from Gavrilov-Shilnikov chaos scenario as pleating of the torus [9]. The process of the deformation is accompanied with the transformations of Fourier spectrum of the intensity. Main harmonics become broadening and combined harmonics originate. In the range of the parameter t /t _f =1.696-1.71 the time dependencies of the intensity demonstrate the evolution from ordinary beatings to very complex dynamical regime.

The process of torus distruction and the conversion into chaotic dynamics completes at t /t _f =1,71. Further increasing of t /t _f leads to the complication of the intensity pulse structure which becomes fully irregular. A number of spectral components of the Fourier spectrum increases and each harmonic become broadened. One can observe absolutely irregular distributions of points at the Poincare maps. Based on mentioned results, we can characterize chaotic lasing within the region of its existence (region III in Fig.1) as the chaos of various degree of the development. Characteristics of lasing at t /t _f =2 are shown in Fig.3d and 5a as the example of developed chaos.

The structure of the vibrations simplifies near the right boundary of the chaotic lasing at t /t _f @ 2,3. Points of Poincare section cluster into groups (it looks like separated spots in Fig 3f) while the Fourier spectrum and time structure of the intensity remain relatively complex (Fig.5c). The simplification of Poincare map indicates the tendency of transformation of chaos into regular regime. If t /t _f reaches the value of t /t _f =2,4 chaotic lasing transforms into quasi-periodical regime and at t /t _f =2,5 into fully regular pulsing. It is interesting to note that such a simplification of Poincare map was also found near the center of the range of chaotic lasing at t /t _f ~ 2,1-2,2 (Fig.3e). Time dependence of the intensity looks like periodical pulsing with period Т» 3,3t _f but it demonstrates very complicated structure. The analysis of corresponding Fourier spectrum (Fig.5b) indicates that the frequencies n ₁ and n ₂ becomes commensurable (7n ₁ = 4n ₂) to within the accuracy obtained in our calculations. Because of this reason the harmonic frequencies locking apparently occurs.

The embedding dimension of an attractor along with the set of Luapunov numbers considered to be used as quantitative characteristic of the disordering of a system [2]. To find the embedding dimension is the important task for distributed system governed by equations similar to (1)-(2) because the dimension value makes clear the number of effective degrees of freedom for the system. This number in turn shows the number of ordinary differential equations needed for full description of the system [2]. In addition the correlative dimension of the attractor was chosen to characterize quantitatively the dynamical regimes. Both the embedding and correlative dimensions were calculated by use of known mathematical procedure invented by P.Grassberger and I.Proccaccia (look, for ins.[2]). Calculated value of the embedding dimension was found minimum at the boundaries of the chaotic lasing region at t /t _f =1,69 and 2,5 where the dynamics of the system is described with the limit cycle (d_e=4 and 5 correspondingly). The value of d_e increases in the regions of quasi-periodical lasing (t /t _f =1,7 and 2,4). The embedding dimension was found to increase further more within the region of chaotic lasing and reach the maximum value d_e=8 in the range of developed chaos (t /t _f =1,8-2). The local decrease of d_e value was observed in the range t /t _f =2,1 - 2,2, where frequencies n ₁ and n are commensurable. The obtained data indicate that the origination of chaotic lasing is associated with the complication of corresponded dynamical system and increasing of the degrees of freedom number. Calculated value of d_e shows that being a distributed system flow laser can be described adequately by means of relatively small amount of ordinary differential equations. The correlative dimension of the attractor d_c was found to be not constant within the region of chaotic lasing. The value of d_c increases in the region of developed chaos to a value of some less then d_c =3. (The dimension d_c =2 in the case of quasi-periodical lasing). Such a behavior of the value of the correlative dimension demonstrates the transformation of the chaotic attractor.

Our calculations show that pumping inhomogeneity doesn't reduce essentially the energy efficiency in this system. The quantum efficiency h of utilization of excitation energy in self-pulsation and chaotic mode of lasing can be quite high for a small dimension of inhomogeneity zone (h₀<<h) and may exceed the value of h ~ 0,6. The similar systems may be applied in practice. The above mentioned method can be used for designing the technological FFL with various lasing regimes. The required control of pumping profile may be technically quite easy performed in case of electric discharge laser with sectioned electrodes

Note that our task was to make clear the general qualitative features of the dynamical behavior of considered systems and calculations were based on highly simplified model. The developed kinetic models of active medium should be applied to predict accurately the performances of real lasers such as СО₂ and СО FFL.

1. Haken G. Lasernaya svetodinamika (М., Мir, 1988) (in russian).

2. Loskutov А.Yu, Michailov А.S. Vvedjenie v sinergetiku. (М., Nauka, 1990) (in russian).

3. Kravtsov N.V., Lariontsev Е.G. Kvantovaja Elektronika, 21, 903 (1994) (in russian).

4. Baranov А.N., Nikolaeva О.Y., Odintsov А.I. Kvantovaya Elektronika, 20, 589 (1993) (in russian).

5. Nikolaeva О.Y., Odintsov A.I.., Fedoseev А.I. Optika i Spekroskopija, 78, 837 (1995) (in russian).

6. Dreizin Yu.А., Dikhne А.М. Pisma v ZhETF, 19, 718 (1974) (in russian).

7. Lichanski V.V., Napartovich А.P. Kvantovaja Elektronika , 7, 237 (1980) (in russian).

9. Аrnold V.I., Аfraimovich V.S., Ilijashenko Y.S., Shilnikov L.P. Teorija bifurkatsij. Dinamitsheskije sistemi (М., VINITI, 1986, т.5, p.2-218) (in russian).