 МОСКОВСКИЙ ГОСУДАРСТВЕHHЫЙ УHИВЕРСИТЕТ
МОСКОВСКИЙ ГОСУДАРСТВЕHHЫЙ УHИВЕРСИТЕТ
имени М.В.ЛОМОHОСОВА
 МОСКОВСКИЙ ГОСУДАРСТВЕHHЫЙ УHИВЕРСИТЕТ
МОСКОВСКИЙ ГОСУДАРСТВЕHHЫЙ УHИВЕРСИТЕТ
имени М.В.ЛОМОHОСОВА
ФИЗИЧЕСКИЙ ФАКУЛЬТЕТ
Кафедpа оптики и спектpоскопии
Специальный оптический практикум
Задача №5
ИЗУЧЕНИЕ СВЕРХТОНКОЙ И ИЗОТОПИЧЕСКОЙ
СТРУКТУРЫ ЛИНИИ РТУТИ l
= 546,1 нм
Методическое пособие для студентов физического факультета
Составители:
Одинцов А.И., Яров А.С.
Москва
2001
СОДЕРЖАНИЕ
1. Сверхтонкая структура в спектрах атомов 2. Изотопический сдвиг уровней и спектральных линий 3. Структура линии ртути l = 546,1 нм 4. Интерферометр Фабри-ПероОсновные спектральные характеристики интерферометра
Расчет интерферограмм
Источник излучения
Оптическая схема установки
Устройство интерферометра Фабри-Перо и его юстировка
Взаимодействие орбитальных и спиновых моментов электронов приводит к возникновению тонкой (мультиплетной) структуры в спектрах атомов, которая во многих случаях может наблюдаться с помощью даже простейшего призменного спектрографа. Типичными примерами мультиплетного расщепления могут служить известный резонансный дублет натрия 32 S1/2 - 32 P1/2, 3/2 и триплет ртути 63 P0,1,2 - 73 S1. Следует отметить, что термин “тонкая структура” является условным. Если дублет натрия действительно состоит из двух близко расположенных линий (589,0 нм и 589,6 нм), то переходы в триплете ртути дают линии 404,7, 435,8 и 546,1 нм с полной шириной триплета 141 нм.
Исследования с помощью спектральных приборов высокого разрешения обнаруживают, что во многих случаях линии мультиплетов в свою очередь обладают сложной структурой. Последняя обусловлена двумя факторами: взаимодействием электронных оболочек атома с магнитными и электрическими моментами ядер, приводящим к сверхтонкой структуре (СТС) уровней, и изотопическим сдвигом уровней для различных изотопов атома. Изучение изотопической и сверхтонкой структуры в спектрах атомов дает ценную информацию о свойствах ядер, в том числе о величинах механических, магнитных и электрических моментов ядер и характере распределения заряда внутри ядра. Одним из важнейших экспериментальных методов в таких исследованиях является оптическая спектроскопия высокой разрешающей силы.
В задаче исследуется сверхтонкая и изотопическая структура линии ртути l = 546,1 нм с использованием интерферометра Фабри-Перо.
1. СВЕРХТОНКАЯ СТРУКТУРА В СПЕКТРАХ АТОМОВ
Спиновые и орбитальные механические моменты входящих в состав ядра протонов и нейтронов формируют спиновый момент ядра ![]() . В соответствии с общими правилами квантования моментов квадрат спинового момента ядра и его проекция на ось z определяются формулами
. В соответствии с общими правилами квантования моментов квадрат спинового момента ядра и его проекция на ось z определяются формулами ![]() ,
, ![]() . Квантовое число I принимает целые значения для ядер с четным массовым числом А и полуцелые для ядер с нечетным А. При этом существенное значение для величины спина ядра имеет не только четность А, но и четность числа протонов и нейтронов в отдельности. В зависимости от сочетания этих величин все ядра делятся на четыре группы: четно-четные, нечетно-нечетные, четно-нечетные и нечетно-четные. Более половины всех устойчивых ядер являются четно-четными и все они в основном состоянии имеют спин I = 0. Нечетно-нечетных стабильных изотопов с целым спином всего 5. Все другие устойчивые ядра относятся к оставшимся двум группам (примерно поровну) и имеют полуцелый спин.
. Квантовое число I принимает целые значения для ядер с четным массовым числом А и полуцелые для ядер с нечетным А. При этом существенное значение для величины спина ядра имеет не только четность А, но и четность числа протонов и нейтронов в отдельности. В зависимости от сочетания этих величин все ядра делятся на четыре группы: четно-четные, нечетно-нечетные, четно-нечетные и нечетно-четные. Более половины всех устойчивых ядер являются четно-четными и все они в основном состоянии имеют спин I = 0. Нечетно-нечетных стабильных изотопов с целым спином всего 5. Все другие устойчивые ядра относятся к оставшимся двум группам (примерно поровну) и имеют полуцелый спин.
Ядра с ненулевым спином обладают магнитными моментами, а ядра с I ³
1 - и электрическими моментами. Эти моменты характеризуются различной мультипольностью ![]() , где l = 1, 2, 3…(диполь, квадруполь, октуполь и т.д.). Ввиду того, что все ядра наряду с осевой симметрией обладают также и центром симметрии, магнитные мультиполи с чётным l и электрические мультиполи с нечётным l существовать не могут. Величины моментов быстро убывают с ростом порядка мультипольности. Реальный вклад в сверхтонкое расщепление уровней атомов дают только магнитный дипольный и электрический квадрупольный моменты.
, где l = 1, 2, 3…(диполь, квадруполь, октуполь и т.д.). Ввиду того, что все ядра наряду с осевой симметрией обладают также и центром симметрии, магнитные мультиполи с чётным l и электрические мультиполи с нечётным l существовать не могут. Величины моментов быстро убывают с ростом порядка мультипольности. Реальный вклад в сверхтонкое расщепление уровней атомов дают только магнитный дипольный и электрический квадрупольный моменты.
По аналогии с магнитными моментами, создаваемыми электронами в атомах, магнитный момент ядра может быть представлен в виде:
![]() (1)
(1)
где Мp - масса протона, gI – так называемый g-фактор ядра, определяемый внутренним строением ядра (по порядку величины он равен 1).
Величину магнитного момента принято характеризовать максимальным значением его проекции, которое соответствует mI = I:
![]() . (1а)
. (1а)
За единицу измерения магнитных моментов ядер принят ядерный магнетон
![]() (2)
(2)
Таким образом, можно написать:
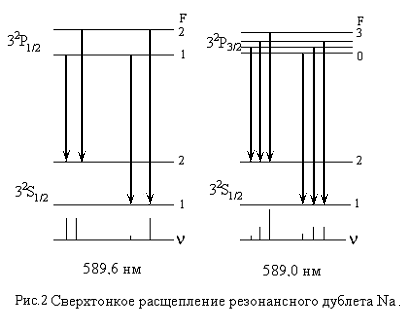
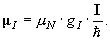 (3)
(3)
![]() . (3а)
. (3а)
По своей величине ядерный магнетон в 1836 раз меньше магнетона Бора ![]() , характеризующего величину магнитных моментов электронов. Малая величина магнитных моментов ядер объясняет узость сверхтонкой структуры спектральных линий, составляющей по порядку величины 10-3 от мультиплетного расщепления.
, характеризующего величину магнитных моментов электронов. Малая величина магнитных моментов ядер объясняет узость сверхтонкой структуры спектральных линий, составляющей по порядку величины 10-3 от мультиплетного расщепления.
Энергия взаимодействия магнитного момента ядра с электронной оболочкой атома равна
![]() (4)
(4)
где ![]() – вектор индукции магнитного поля, создаваемого электронами в точке, где находится ядро (в этом приближении ядро считается точечным магнитным диполем). Магнитное поле
– вектор индукции магнитного поля, создаваемого электронами в точке, где находится ядро (в этом приближении ядро считается точечным магнитным диполем). Магнитное поле ![]() пропорционально электронному магнитному моменту
пропорционально электронному магнитному моменту ![]() атома, который в свою очередь пропорционален механическому моменту атома
атома, который в свою очередь пропорционален механическому моменту атома ![]() ,
, ![]() , где gJ – g-фактор атомного уровня. При этом вектор
, где gJ – g-фактор атомного уровня. При этом вектор ![]() антипараллелен
антипараллелен ![]() и может быть представлен как
и может быть представлен как ![]() /ħJ. Подставляя это выражение вместе с (3) в формулу (4) запишем её в виде:
/ħJ. Подставляя это выражение вместе с (3) в формулу (4) запишем её в виде:
![]() /ħ2, (5)
/ħ2, (5)
где А – постоянная сверхтонкой структуры атомного уровня, равная
![]() (6)
(6)
Вследствие магнитного взаимодействия вектора ![]() и
и ![]() складываются в вектор полного момента атома
складываются в вектор полного момента атома ![]() . С наглядной точки зрения это означает, что векторы
. С наглядной точки зрения это означает, что векторы ![]() и
и ![]() совместно прецессируют вокруг
совместно прецессируют вокруг ![]() (рис. 1). Длина вектора
(рис. 1). Длина вектора ![]() квантуется по соотношению
квантуется по соотношению ![]() =ħ2 F(F+1). Квантовое число F при данных значениях чисел I и J определяет взаимную ориентацию векторов моментов I и
=ħ2 F(F+1). Квантовое число F при данных значениях чисел I и J определяет взаимную ориентацию векторов моментов I и ![]() , при этом
, при этом
![]() (7)
(7)
Подставляя это выражение в (5), получаем формулу для сверхтонкого расщепления, обусловленного магнитным моментом ядра:
![]() (8)
(8)
Квантовое число F принимает значения:
F = I+J, I+J-1, ..., |I-J|, (9)
т.е. (2J+1) значений при I ³
J и (2I+1) значений при I ![]() J. Уровень с заданным J расщепляется на соответствующее число подуровней сверхтонкой структуры, причем интервал между соседними подуровнями равен
J. Уровень с заданным J расщепляется на соответствующее число подуровней сверхтонкой структуры, причем интервал между соседними подуровнями равен
![]() (10)
(10)
Таким образом, величина интервала d
EF,F+1 пропорциональна (F+1) – это так называемое правило интервалов для СТС, аналогичное соответствующему правилу для мультиплетного расщепления. Для ядер с отрицательным магнитным моментом ![]() (в случае
(в случае ![]() ) постоянная А <
0. При этом согласно (8) наблюдается обращённый порядок уровней СТС – уровни с большими значениями F лежат ниже.
) постоянная А <
0. При этом согласно (8) наблюдается обращённый порядок уровней СТС – уровни с большими значениями F лежат ниже.
В соответствии с (6) постоянная А пропорциональна величине магнитного поля, создаваемого электронами в месте расположения ядра. Наибольшее магнитное поле создают неспаренные s-электроны, которые располагаются ближе всего к ядру. Поэтому следует ожидать, что сверхтонкое расщепление будет наиболее значительным для тех уровней, электронные конфигурации которых содержат неспаренный s-электрон. По сравнению с постоянной спин-орбитального взаимодействия в атомах постоянная А очень мала. Обычно она лежит в пределах 10-3-10-1 см-1, и лишь в у тяжелых элементов может приближаться к 1 см-1.
Наблюдаемая СТС спектральных линий атомов соответствует переходам между подуровнями СТС верхнего и нижнего уровней. (В радиочастотной области спектра наблюдаются магнитные дипольные переходы между подуровнями сверхтонкой структуры, принадлежащими одному расщеплённому уровню.) Правило отбора для переходов имеет вид
ΔF = 0, ±1. (11)
Теоретические значения интенсивностей компонент сверхтонкой структуры подчиняются правилу сумм интенсивностей, которое (с заменой квантового числа F на J) имеет место и в мультиплетной структуре атомов [1]. Согласно этому правилу сумма интенсивностей компонент, имеющих общий уровень, пропорциональна статистическому весу данного уровня. Таким образом, справедливы соотношения
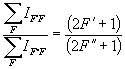 . (12)
. (12)
(При этом оба уровня ![]() и
и ![]() должны относиться либо к верхним, либо к нижним уровням переходов.) В простых случаях (не всегда) из подобных соотношений удаётся рассчитать относительные интенсивности компонент СТС.
должны относиться либо к верхним, либо к нижним уровням переходов.) В простых случаях (не всегда) из подобных соотношений удаётся рассчитать относительные интенсивности компонент СТС.
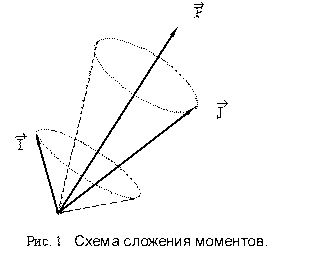
В качестве примера на рис. 2 показано сверхтонкое расщепление уровней и линий резонансного дублета натрия. Натрий (Z = 11) имеет единственный стабильный изотоп с А=23. Ядро Na23 является нечетно-четным и обладает спином I =3/2. Магнитный момент его равен 2,217μN. Общий нижний уровень обеих компонент дублета 32S1/2 расщепляется на два сверхтонких подуровня с F = 1 и 2. Уровень 32P1/2 расщепляется на 2 (F=1,2), а уровень 32Р3/2 на четыре подуровня (F=0,1,2,3). Величина расщепления нижнего уровня 32S1/2 равняется 0,095 см-1. Расщепление верхнего Р-состояния намного меньше: для уровня 32P1/2 оно равно 0,006 см-1, полное расщепление уровня 32Р3/2 составляет 0,0035см-1.

Рассмотрим теперь энергию взаимодействия электронной оболочки атома с электрическим квадрупольным моментом ядра, который возникает из-за отклонения формы ядра от сферически симметричной. Электрическое поле вытянутого или сплюснутого ядра можно представить как наложение поля равномерно заряженной сферы и поля положительных и отрицательных зарядов, расположенных у поверхности сферы и образующих систему, близкую к квадруполю (рис.3). Квадрупольный момент такого ядра Q определяется формулой
![]() (13)
(13)
где r
– плотность электрического заряда в точке с координатами (x
, h
, z
), находящейся на расстоянии r от центра ядра. Ось симметрии ядра, совпадающая с направлением механического момента, выбрана за ось ![]() z
. Квадрупольный момент ядра характеризуется величиной Q, имеющей размерность площади. По порядку величины он обычно составляет
z
. Квадрупольный момент ядра характеризуется величиной Q, имеющей размерность площади. По порядку величины он обычно составляет ![]() . Для вытянутого ядра квадрупольный момент положителен, для сплюснутого - отрицателен (рис.3 а, б).
. Для вытянутого ядра квадрупольный момент положителен, для сплюснутого - отрицателен (рис.3 а, б).
Взаимодействие квадрупольного момента ядра с неоднородным электрическим полем электронной оболочки атома приводит к дополнительной энергии взаимодействия ΔE(Q) [1,5]. Её величина зависит от ориентации ядра по отношению к направлению градиента электрического поля в месте расположения ядра, т.е. от взаимной ориентации векторов ![]() и
и ![]() . Поэтому энергия квадрупольного взаимодействия имеет различные значения для уровней сверхтонкой структуры с разными F.
. Поэтому энергия квадрупольного взаимодействия имеет различные значения для уровней сверхтонкой структуры с разными F.
Квантово-механический расчёт даёт следующее выражение для энергии квадрупольного взаимодействия [1]:
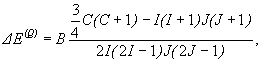 (14)
(14)
где С=F(F+1) - I(I+1) - J(J+1), В – постоянная квадрупольного взаимодействия, пропорциональная величине Q и градиенту внутриатомного электрического поля. Эта постоянная для атомов имеет порядок 10-4 - 10-2 см-1. Обычно она значительно меньше, чем А, но не настолько мала, чтобы ею можно было пренебречь. Есть случаи, когда А и В по порядку величины сравнимы. Заметим, что s-электроны, как и все электроны заполненных электронных оболочек атома, не участвуют в квадрупольном взаимодействии, так как они создают сферически симметричное распределение заряда.
В общем случае для ядер с I ³
1 СТС уровней определяется как магнитным, так и квадрупольным взаимодействием ![]() . При этом правило интервалов (10) нарушается или выполняется лишь приближенно.
. При этом правило интервалов (10) нарушается или выполняется лишь приближенно.
2. ИЗОТОПИЧЕСКИЙ СДВИГ УРОВНЕЙ И СПЕКТРАЛЬНЫХ ЛИНИЙ
Важную роль в спектроскопии играют изотопические эффекты, проявляющиеся в зависимости энергии уровней атома от массы и размеров ядра. Величины изотопического сдвига и сверхтонкого расщепления могут быть одного порядка. Примером этого является исследуемая в данной задаче линия ртути.
У легких элементов изотопическое смещение обусловлено зависимостью энергии уровней от массы ядра. Этот так называемый массовый эффект возникает вследствие движения ядра вокруг общего центра масс атома. Наиболее просто влияние конечной массы ядра можно учесть для водородоподобных атомов. При этом постоянная Ридберга R заменяется на величину
![]() (15)
(15)
где M – масса ядра. Разность энергий уровней изотопов с массами М1 и М2:
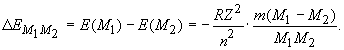 (16)
(16)
Таким образом, уровни более тяжелого изотопа смещаются вниз по отношению к уровням более легкого изотопа. Такое направление изотопического смещения принято считать положительным. Из (16) вытекает величина смещения спектральных линий изотопов:
![]() (17)
(17)
Изотопическое смещение уровней и линий быстро убывает с увеличением массы ядра, приблизительно как 1/М2. Наибольшая величина сдвига наблюдается у водорода, где смещение линии Нb дейтерия относительно водорода составляет 5,6 см-1. В средней части периодической системы (А~100) смещение линий в видимой области спектра имеет порядок 10-3см-1, что находится на пределе возможностей их экспериментального обнаружения.
Формулы (15) - (17) описывают так называемый нормальный массовый эффект. В атомах с двумя и более внешними электронами дело обстоит сложнее: взаимная связь движения электронов приводит к появлению дополнительного специфического массового эффекта, зависящего от состояния электронной оболочки атома.
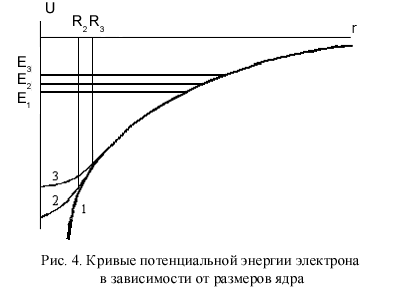
В нижней части периодической системы, начиная примерно с А~140, изотопические смещения снова начинают возрастать. Это явление имеет совсем иную физическую основу: оно обусловлено влиянием на энергетические уровни конечного объема ядра – объемный эффект в изотопическом смещении.
На рис. 4 кривая 1 изображает кулоновскую потенциальную энергию электрона в поле точечного ядра. В случае ядер конечного размера с тем же Z потенциал внутри ядра будет отличаться от кулоновского, притом тем больше, чем больше радиус ядра R (кривые 2 и 3). В предположении, что заряд равномерно распределен по объему ядра сферической формы, потенциальная энергия электронов внутри ядра равна:
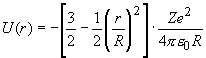 , (18)
, (18)
где согласно капельной модели ядра R = R0A1/3, R0≈1,2× 10-13 см. Для электронов, проникающих внутрь ядра, увеличение потенциальной энергии при r < R приводит к ослаблению связи электрона с ядром. В результате энергетический уровень электрона смещается вверх. На рис. 4 уровни E1, E2, E3 соответствуют потенциальным кривым 1, 2, 3. Таким образом, уровни изотопа с большим R располагаются выше. Иными словами, объемный эффект, в отличие от массового, приводит к отрицательным сдвигам уровней. Наибольший вклад в объемный сдвиг дают s-электроны, которые имеют наибольшую вероятность проникновения внутрь ядра. Величина сдвига быстро растет с ростом заряда ядра Z.
Исследование изотопических смещений в оптических спектрах имеет важное значение как источник информации о строении атомных ядер. В практическом плане изотопный спектральный анализ широко используется для определения количественного содержания изотопов в естественных и искусственных смесях.
3. СТРУКТУРА ЛИНИИ РТУТИ l = 546,1 нм
Естественная ртуть (Z=80) содержит смесь устойчивых изотопов со следующим процентным содержанием [7]:
Массовое число 196 198 199 200 201 202 204
% 0,146 10,02 16,84 23,13 13,22 29,80 6,85
Для нечётных изотопов значения спинов и магнитных моментов составляют
Hg199 ![]() m
= 0,5027m
N
m
= 0,5027m
N
Hg201 ![]() m
= -
0,5567m
N
m
= -
0,5567m
N
Изотоп Hg201 обладает также квадрупольным моментом Q=0,45. 10-24 см2 [7]. Чётные изотопы имеют нулевой спин.
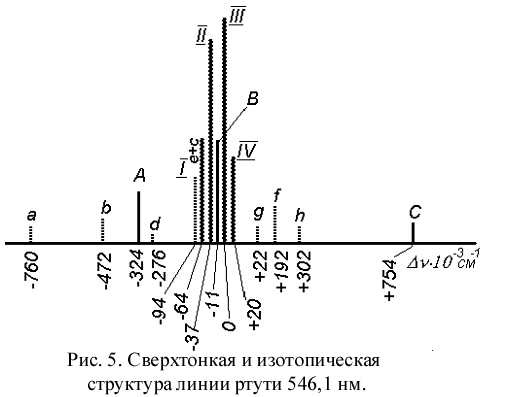
За исключением изотопа Hg196 с малым процентным содержанием, спектральные линии остальных изотопов достаточно интенсивны. Линия l =546,1 нм, возникающая в результате перехода 63Р2 – 73S1, входит в число наиболее сильных и хорошо изученных линий ртути. Она подробно исследовалась в целом ряде работ (см., например, [6]). Структура линии приведена на рис. 5. Чётные изотопы Hg198, Hg200, Hg202 и Hg204 дают четыре интенсивных компоненты в центре линии обозначенные на схеме римскими цифрами I, II, III и IV. (Компонента изотопа Hg196 не наблюдается из-за её малой интенсивности.) Изотоп Hg199, обладающий спином I=1/2, даёт три компоненты сверхтонкой структуры, указанные буквами А, В и С. Изотоп Hg201 со спином I=3/2 даёт 8 компонент a, b, c, d, e, f, g, h. Причём компоненты c и e накладываются друг на друга. Таким образом, всего в данной линии насчитывается 14 компонент.
Величина изотопического сдвига уровней для нечетных изотопов определяется по положению “центра тяжести” их сверхтонкого расщепления:
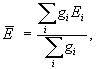 (19)
(19)
где суммирование проводится по всем подуровням сверхтонкой структуры с энергией Еi и статистическим весом gi=2Fi + 1. Разность энергий центров тяжести верхнего и нижнего уровней (в см-1) определяет частоту ![]() , соответствующую центру тяжести компонент структуры спектральной линии
, соответствующую центру тяжести компонент структуры спектральной линии
![]() . (20)
. (20)
Величина ![]() может быть также найдена непосредственно по частотам n
i компонент СТС по соотношению
может быть также найдена непосредственно по частотам n
i компонент СТС по соотношению
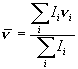 , (21)
, (21)
где Ii – относительные интенсивности компонент. В (21) рекомендуется использовать теоретические значения интенсивностей, определяемые с помощью правила сумм (12) или по специальным формулам [1], так как экспериментальные значения Ii могут быть искажены под влиянием реабсорбции в источнике и за счёт других факторов. Найденные таким образом центры тяжести компонент изотопов Hg199 и Hg201 оказываются расположенными между компонентами соседних чётных изотопов, причём заметно смещены к изотопу с меньшим массовым числом.
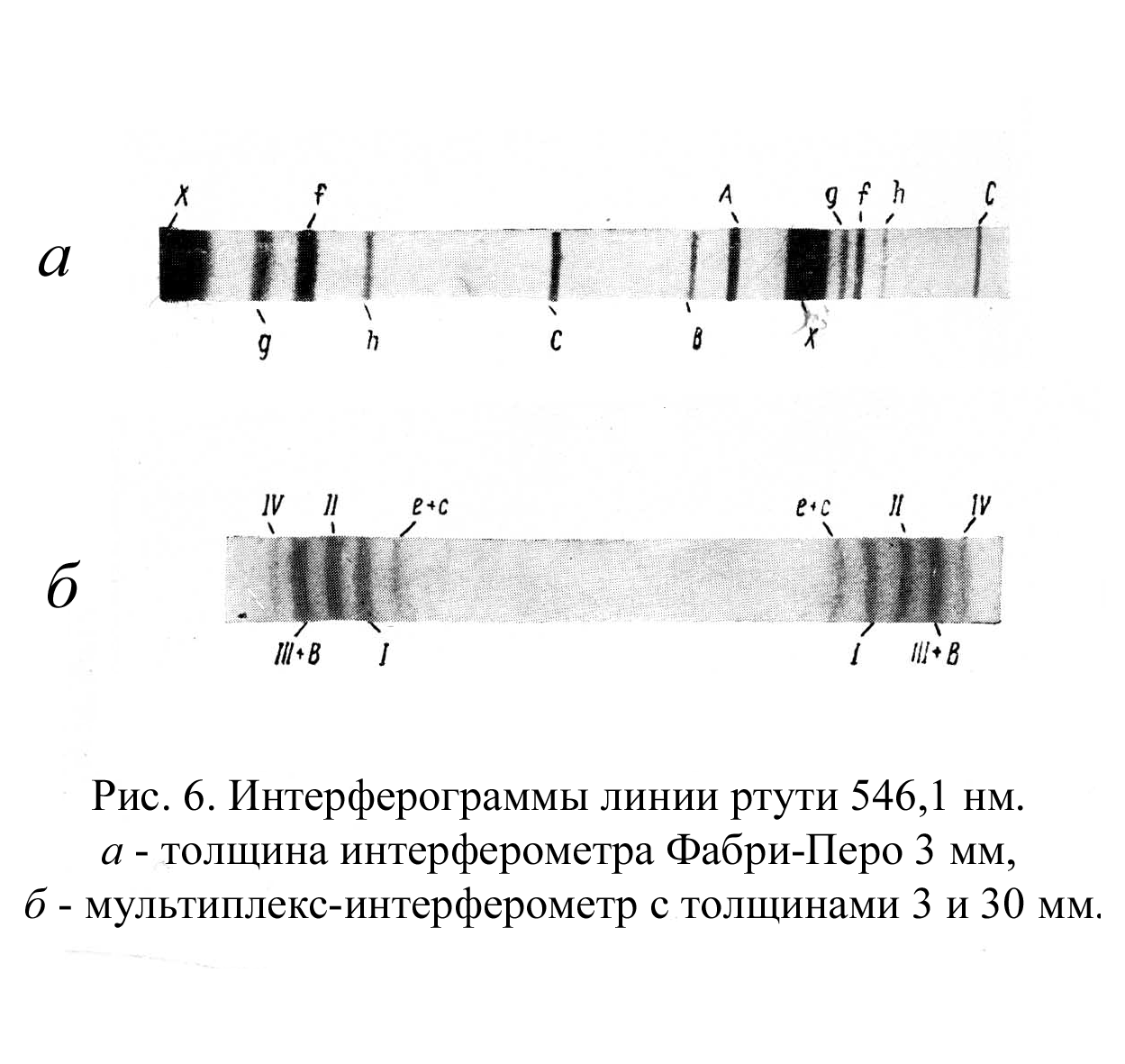
На рис.6 (а,б) приведены фотографии спектров линии ртути l =546,1 нм, полученные с помощью интерферометра Фабри-Перо [6]. На рис. 6а видны два односторонних порядка интерференционных колец. При толщине интерферометра d = 3мм, область дисперсии интерферометра немного превышает частотное расстояние между крайними компонентами а и C линии (рис.5). Компоненты а и d, вследствие их малой интенсивности, не наблюдаются. Группа центральных компонент в данном случае сливается в одну широкую линию, обозначенную через Х. Используя мультиплекс – интерферометр (см. далее) и ртутную лампу специальной конструкции, дающую узкие линии, оказалось возможным разрешить эту группу компонент (рис. 6б). Здесь, в отличие от рис. 6а, показаны симметричные участки одного порядка, ближайшего к центру. Заметим, что для компонент a, b, A и d в данном порядке не выполняется условие максимума интерференции, компоненты g, f, h, С выходят за пределы рисунка.
Интерферометр (эталон) Фабри-Перо, несмотря на простоту устройства, обладает наиболее высокой разрешающей силой среди существующих оптических спектральных приборов. Действие его основано на интерференции большого числа лучей, получаемых при многократном отражении световой волны между двумя параллельно расположенными плоскими зеркалами, обладающими частичным пропусканием. В современных интерферометрах используют многослойные диэлектрические зеркальные покрытия, которые наносятся в вакууме на подложки из стекла или кварца. При этом может быть достигнут высокий коэффициент отражения при поглощении в слоях менее 0,5%. К качеству поверхности зеркал предъявляются очень высокие требования: их плоскость в лучших образцах выдерживается с точностью до (0,02 ¸ 0,01)l .
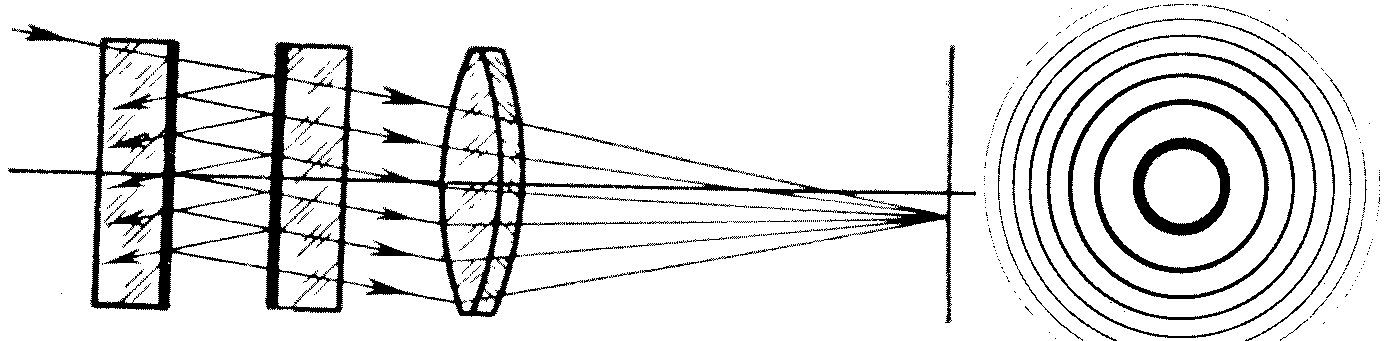
Рис. 7 Схема интерферометра Фабри-Перо
На рис. 7 изображена принципиальная схема интерферометра. Условие максимума интерференции имеет вид:
![]() , (22)
, (22)
где d – расстояние между пластинами, называемое толщиной интерферометра), j – угол отражения лучей от зеркал, m – целое число (порядок интерференции). Показатель преломления воздуха мы полагаем n=1. При освещении интерферометра монохроматическим светом в фокальной плоскости линзы, установленной на выходе интерферометра, наблюдаются концентрические интерференционные кольца равного наклона (рис.7).
Суммирование амплитуд всех выходящих из интерферометра лучей дает распределение интенсивности в интерференционной картине, которое имеет вид
![]() (23)
(23)
где r
– расстояние от центра системы колец, I0 – интенсивность падающего света, r и Т – коэффициенты отражения и пропускания (по интенсивности) зеркал интерферометра, ![]() – фазовый сдвиг между соседними лучами,
– фазовый сдвиг между соседними лучами, ![]() , где f – фокусное расстояние линзы. Функция I(r
) для монохроматического излучения является аппаратной функцией интерферометра Фабри-Перо.
, где f – фокусное расстояние линзы. Функция I(r
) для монохроматического излучения является аппаратной функцией интерферометра Фабри-Перо.
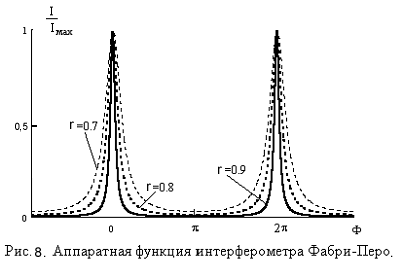
На рис. 8 приведен вид аппаратной функции, рассчитанной по формуле (23), для различных r. Видно, что с увеличением коэффициента отражения зеркал интерференционные кольца становятся все более резкими.
Основные спектральные характеристики интерферометра
Дисперсия. Выражение для угловой дисперсии интерферометра можно получить, дифференцируя (22) по l :
![]() (24)
(24)
Из (24) видно, что дисперсия не зависит от толщины интерферометра. С уменьшением угла j она возрастает и стремится к бесконечности при j ® 0. Направление дисперсии таково, что при фиксированном порядке интерференции m большим длинам волн соответствуют меньшие значения j .
Область дисперсии. Если интерферометр освещается немонохроматическим светом, соответствующим участку спектра между l и l ¢ , то вследствие дисперсии интерференционные кольца будут расширены. При некотором значении D l = l - l ¢ ширина колец станет равна расстоянию между соседними порядками интерференции и интерференционная картина исчезнет. Указанный интервал длин волн D l , определяющий максимальную ширину участка спектра, в пределах которой интерферометр может работать без переналожения порядков интерференции, называется областью дисперсии интерферометра.
Пусть при некотором значении j максимум интерференции порядка m для длины волны l совпадает с максимумом порядка m+1 для длины волны l ¢ . Согласно (22) это означает (m+1) l ¢ =ml . Отсюда для области дисперсии D l = l - l ¢ имеем
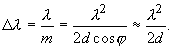 (25)
(25)
Угол j обычно не превышает нескольких градусов, поэтому сosj » 1. Выражение для области дисперсии в частотах (волновых числах) имеет вид
![]() (26)
(26)
Например, для интерферометра с d = 1 см область дисперсии равна D n = 0,5 см-1. Малая величина области дисперсии интерферометра Фабри-Перо требует применения дополнительного монохроматора, выделяющего из спектра источника исследуемый участок. В качестве последнего обычно используется призменный или дифракционный спектрограф в схеме скрещенной дисперсии, когда дисперсия интерферометра направлена вдоль спектральных линий, т.е. перпендикулярно направлению дисперсии спектрографа.
Разрешающая способность. Интерферометр Фабри-Перо достаточно надежно разрешает две близкие по интенсивности спектральные компоненты, частотный интервал между которыми равен аппаратной ширине интерференционного максимума d n , измеренной на половине его высоты. Эту величину и принимают в качестве предела разрешения интерферометра. Используя (23) для величины d n можно получить выражение
![]() (27)
(27)
Величину Nэфф =![]() называют эффективным числом интерферирующих лучей. Разрешающая способность интерферометра
называют эффективным числом интерферирующих лучей. Разрешающая способность интерферометра
![]() (28)
(28)
где m – порядок интерференции. Так, для интерферометра с d = 1 см и r = 0,9 в случае l = 5´ 10-5 см имеем: m = 4× 104, Nэфф = 29, d n = 0,017 см-1 и R = 1,2× 106. Реальная разрешающая способность интерферометра может быть существенно меньше теоретической вследствие дефектов поверхностей зеркал, погрешностей юстировки и других факторов.
В спектроскопических исследованиях находят применение интерферометры Фабри-Перо с толщинами 10-15 см и даже более, с помощью которых удаётся достичь разрешения ~10-3 см-1. Область дисперсии таких приборов часто оказывается меньше полной ширины исследуемой спектральной линии. В этих случаях используют систему из двух последовательно расположенных интерферометров с разными толщинами, получившую название мультиплекс-интерферометра [4]. Вспомогательный “тонкий” интерферометр осуществляет предварительную монохроматизацию излучения в пределах ширины линии (направления дисперсии обоих интерферометров совпадают). Соотношение толщин интерферометров выбирают кратным, например, 1:10.
Контрастность. Контрастность интерферометра g определяется как отношение интенсивностей в максимуме и минимуме аппаратной функции. Из (23) легко получить
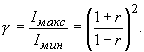 (29)
(29)
Ниже приведены величины Nэфф и g для различных значений коэффициента отражения зеркал:
r, % 80 85 90 95 97 98
Nэфф 14 19 29 61 103 155
g 81 152 361 1521 4320 9800
Расчет интерферограмм
Полагая в формуле (22) cosj » 1-j 2/2, можно получить выражение для разности частот компонент n и n ¢ линии, принадлежащих одному порядку интерференции m:
![]() (30)
(30)
где Dm и Dm¢ -диаметры интерференционных колец, f – фокусное расстояние проектирующего объектива. Величину f можно исключить, воспользовавшись аналогичным соотношением для области дисперсии
![]() (31)
(31)
где Dm и Dm+1 – диаметры колец соседних порядков для одной компоненты. Объединяя (30) и (31), имеем
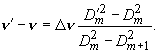 (32)
(32)
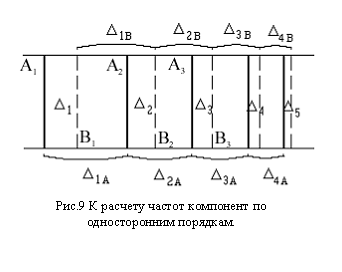
Более простым и удобным является метод обработки интерферограмм с использованием односторонних порядков интерференции. При этом не требуется измерять полные диаметры колец, а достаточно определить относительные положения компонент в нескольких порядках интерференции по одну сторону от центра системы колец. Пусть А1, А2, А3 – положения компоненты с частотой n в последовательных порядках интерферограммы (рис.9); В1, В2, В3,... то же для другой компоненты с частотой n ¢ , D 1А, D 2А, … и D 1В, D 2В, … – расстояния между соседними порядками; D 1, D 2, … – расстояния между компонентами А и В в одном порядке. Для порядков, достаточно удаленных от центра картины, частотный интервал между компонентами с хорошим приближением может быть определен по формуле
![]() (33)
(33)
которая получается из (32) при условии Dm-Dm+1 << Dm .
В условиях данной задачи удовлетворительная точность расчётов получается при использовании односторонних колец, начиная с четвертого (от центра картины). В обоих вариантах расчета полученные результаты усредняют по нескольким порядкам.
5. ЭКСПЕРИМЕНТАЛЬНАЯ УСТАНОВКА
В задаче изучается структура линии ртути l = 546,1 нм, возбуждаемой высокочастотным разрядом, с использованием в качестве прибора высокой разрешающей силы интерферометра Фабри-Перо.
Источник излучения
Спектр возбуждается в безэлектродной ртутной лампе типа ВСБ-2 с помощью прибора питания ППБЛ-3, конструктивно выполненного в виде двух раздельных блоков – генератора высокой частоты и выпрямителя. Генератор предназначен для возбуждения ламп типа ВСБ-2 электромагнитным полем высокой частоты. Он находится в цилиндрическом кожухе, закрепленном на стойке. Собственно источник излучения – безэлектродная лампа и анодный контур размещаются в специальной камере, изолированной от электрического монтажа. Лампа представляет собой полый стеклянный шарик, наполненный инертным газом и содержащий некоторое количество паров ртути с низким парциальным давлением. Камера с анодным контуром и лампой закрывается съемной крышкой, в которой имеется окно диаметром 20 мм. Номинальное значение частоты генератора 110 МГц. Электропитание генератора осуществляется от выпрямителя. Выходная мощность последнего плавно регулируется изменением анодного тока. Контроль тока производится по миллиамперметру, установленному на панели выпрямителя. Номинальное значение тока для ртутной лампы - 50 mА. Конструкция лампы предусматривает воздушное охлаждение.
Оптическая схема установки
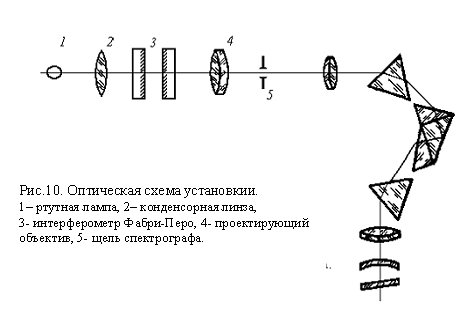
В данной задаче применяется схема скрещенной дисперсии - комбинация интерферометра Фабри-Перо с призменным спектрографом. Оптическая схема установки изображена на рис.10. В качестве монохроматора используется трехпризменный спектрограф ИСП-51 с фокусным расстоянием камеры f=270мм, имеющий в зеленой области спектра дисперсию порядка 6 нм/мм. Применяется внешняя установка интерферометра. Возможен другой вариант оптической схемы, при котором интерферометр Фабри-Перо устанавливается в параллельном пучке между коллиматорным объективом и диспергирующей системой призменного или дифракционного спектрографа. Преимущество такой схемы состоит в том, что она не требует создания параллельного пучка вне спектрографа.
Излучение ртутной лампы 1 с помощью конденсорной линзы 2 с фокусным расстоянием f = 9см направляется на интерферометр Фабри-Перо 3 в виде приблизительно параллельного пучка. Объектив 4 с f=30 см проектирует интерференционные кольца на щель спектрографа 5. Системы интерференционных колец для разных длин волн перекрываются, образуя сплошную картину. Щель “вырезает” прилегающие к вертикальному диаметру участки колец. В фокальной плоскости спектрографа (на фотопластинке) образуется серия изображений щели с отрезками интерференционных колец.
Устройство интерферометра Фабри-Перо и его юстировка
Схема используемого в данной работе интерферометра ИТ-51-30 приведена на рис.11. Пластины 1 с зеркальными покрытиями разделены промежуточным кольцом 2, имеющим с каждой стороны по три опорных выступа 3. Расстояние между противоположными выступами выдержано с точностью до 1 мкм. Прибор снабжен набором таких колец с толщинами от 0,3 до 30 мм. Кольца с толщиной до 6 мм изготовлены из инвара, свыше 6 мм – из плавленого кварца; оба материала имеют малый коэффициент термического расширения. Каждому промежуточному кольцу придается соответствующее дополнительное кольцо 4 из инвара. В данной задаче толщина интерферометра равняется 4 мм.
Многослойные диэлектрические покрытия зеркал обеспечивают коэффициент отражения в зеленой области спектра 92%. Пластины имеют небольшой клин (~30¢ ). Это позволяет уводить в сторону вторичную интерференционную картину, возникающую вследствие отражения выходящего пучка от наружной поверхности пластины изнутри (r~4%) и затем от зеркальной поверхности той же пластины. Корпус интерферометра 7 установлен на столике 8, позволяющем регулировать наклон оси интерферометра в горизонтальном и вертикальном направлениях.
Юстировку пластин на параллельность производят с помощью трех юстировочных винтов 5, которые через пружинящие пластинки 6 осуществляют нажим на переднюю пластину интерферометра, при этом выступы промежуточных колец слегка деформируются. Контроль юстировки производится путем наблюдения колец непосредственно на выходе интерферометра. Если пластины не строго параллельны и образуют клин, то при перемещении глаза от вершины к основанию клина, кольца будут как бы “расходиться” из центра, а при обратном движении – стягиваться к центру. Интерферометр можно считать отъюстированным, если по всей поверхности пластин диаметры колец одинаковы и, следовательно, не изменяются при перемещении глаза в любом направлении. Однако если поверхности пластин интерферометра имеют отклонения от плоскости (например, обе они выпуклые), идеального постоянства диаметра колец добиться не удается. В этом случае на практике обычно используют лишь центральную часть пластин, диафрагмируя периферийную зону.
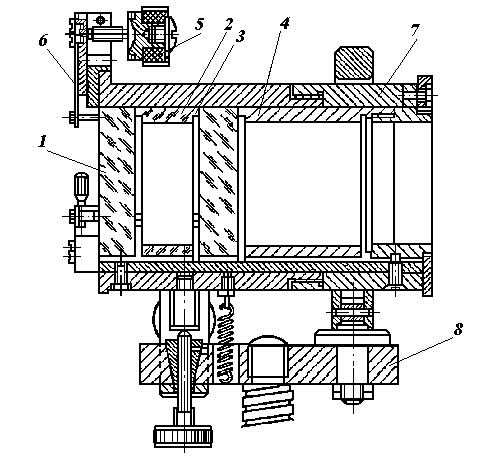
Рис.11. Устройство интерферометра Фабри-Перо ИТ-51-30
1- пластины с зеркальным покрытием, 2- промежуточное кольцо, 3- опорные выступы, 4- дополнительное кольцо, 5- юстировочные винты, 6- пружины, 7- корпус, 8- столик.
Обработка интерферограмм
Интервалы между компонентами исследуемой линии измеряются с помощью измерительного микроскопа МИР-12 или компаратора ИЗА-2 (точность измерения 0,01 мм). Для обработки интерферограмм можно также использовать столик для просмотра спектрограмм СТЛ и микрофотометр МФ-2, который в некоторых случаях обеспечивает более точное нахождение максимумов спектральных компонент. При обработке необходимо измерить положения всех зафиксированных на пластинке компонент структуры. Расчет частотных интервалов между компонентами производится методом односторонних полос. Результаты усредняют по 3-4 порядкам. Находят среднюю ошибку измерений.
для уровня 63Р2 А= - 0,1119 см-1, В=0,0130 см-1;
для уровня 73S1 А= - 0,2656 см-1, В=0.
Построить схему уровней СТС и переходов. Отождествить на схеме приведенные на рис. 5 компоненты структуры линии и экспериментально наблюдаемые переходы.
8. ПРАВИЛА ТЕХНИКИ БЕЗОПАСНОСТИ
Основная:
Дополнительная: