Московский Государственный Университет им. М.В.Ломоносова
Физический факультет
Кафедра оптики и спектроскопии
Структура фазовых сингулярностей в многомодовых лазерных пучках
Лабораторная задача № 28
Авторы
:Макаров В. Г.,
Короленко П. В.,
Полоско А. Т.
Москва
2000
Часть
I. Общетеоретические сведения§ 1
.1. Природа фазовых сингулярностей, типы дислокаций волнового фронтаФазовые сингулярности в пучках когерентного излучения обусловлены нарушением топологической структуры волнового фронта и характеризуются аномально-быстрыми изменениями фазы световых колебаний. На волновом фронте фазовые сингулярности очень часто проявляются в форме винтовых дислокаций (ВД). Впервые ВД волнового фронта были замечены при анализе структуры волнового фронта спекловых полей, полученных при пропускании лазерного пучка через фазовые пластинки.
Винтовыми дислокациями называются точки фронта волны, при обходе вокруг которых в плоскости, перпендикулярной к направлению распространения, фаза световых колебаний
изменяется на величину 2p l, где l - целое число, отличное от нуля. Величина l называется порядком дислокации или топологическим зарядом поверхности волнового фронта. В зависимости от направления закрутки “винта” волновой поверхности ВД подразделяются на левые (отрицательные) и правые (положительные).Амплитуду центрально-симметричного поля в области дислокации первого порядка (
при r = 0 ) можно представить в виде:![]() , (1.1.1)
, (1.1.1)
где a - азимутальный угол.
Амплитуда поля вблизи ВД более высоких порядков описывается выражением
:![]() , (1.1.2)
, (1.1.2)
где
l - порядок дислокации.Появление ВД кардинальным образом меняет топологию волнового фронта. Эквифазная поверхность перестает быть многозначной
(см. рис.1.1,а) и осуществляется переход к единой поверхности со специфической волновой структурой. Это иллюстрирует рисунок (1.1,б), на котором изображен волновой фронт лазерного пучка с ВД, расположенной на оси. Направление распространения световой энергии задается вектором Умова-Пойнтинга, перпендикулярным, как известно, поверхности волнового фронта в каждой точке. Следовательно, в окрестности ВД будет происходить завихрение энергетического потока.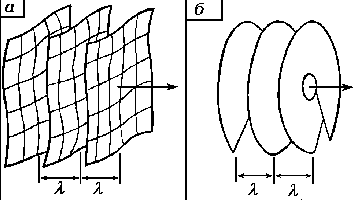
Рисунок 1.
1. Структура волновых фронтов в отсутствие (а) и при наличии винтовой дислокации (б) ( l - длина волны излучения).Важным для практики частным случаем ВД является так называемая краевая дислокация КД. Она представляет собой линию в поперечном сечении пучка, на которой поле меняет скачком свою фазу на p . ВД можно получить сложением двух полей с ортогональными КД, сдвинутых по фазе на
Винтовые дислокации можно представить как точку пересечения линий смены знака действительной и мнимой частей амплитуды поля. Разложим компоненты комплексной амплитуды поля Е на действительную
Re и мнимую Im части, и построим линии, где Re и Im обращаются в нуль (рис. 1.2). Если это не просто линии нуля Re и Im частей, но и линии смены их знака, то точки их пересечения суть точки винтовых дислокаций фазы. Таким образом, там где располагается ВД, амплитуда всегда равна нулю. Когда нулевые линии действительной и мнимой частей не просто пересекаются, но и совпадают на некотором участке, там получается КД.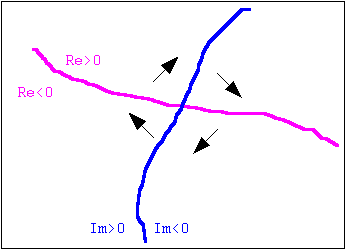
Рисунок 1.2.
Представление ВД как точки пересечения линий смены знака действительной и мнимой частей амплитуды поля. Стрелки показывают изменение фазы поля в различных областях.
§ 1.2. Амплитудно-фазовая структура лазерных пучков. Моды свободного пространства
ВД волнового фронта могут формироваться в пучках когерентного излучения при их распространении через оптические неоднородные среды, при отражении от неровных поверхностей, при прохождении через специально изготовленные голограммы, а также в результате интерференции различных мод (типов колебаний), формирующих данный пучок. Рассмотрим последний процесс более подробно. Сделаем это на примере лазерного излучения, образованного модами Эрмита-Гаусса или Лагерра – Гаусса. Под модой понимается волновой пучок, который сохраняет в процессе распространения форму распределения амплитуды и фазы световых колебаний в поперечном сечении. Моды Эрмита-Гаусса и Лагерра – Гаусса сохраняют свою форму при распространении в свободном пространстве и внутри устойчивого резонатора с большой апертурой зеркал. Пространственное распределение амплитуды поля моды Эрмита-Гаусса, распространяющейся вдоль оси
z, определяется произведением полиномов Эрмита и функции Гаусса: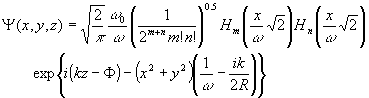 , (1.2.1)
, (1.2.1)
где
Hm() - полином Эрмита, m и n - поперечные индексы моды, указывающие на количество нулей вдоль поперечных осей x и y соответственно, k - волновое число, w 0 и w радиусы пучка в перетяжке и плоскости z=const, R - радиус кривизны волнового фронта, F - фазовый сдвиг между волновым пучком и идеальной плоской волной: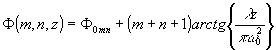 , (1.2.2)
, (1.2.2)
где F
0mn - начальная фаза.Радиус пучка w
0 в перетяжке, радиус пучка w и радиус кривизны волнового фронта R связаны по закону: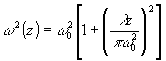 , (1.2.3)
, (1.2.3)
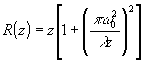 . (1.2.4)
. (1.2.4)
Моды Лагерра – Гаусса используются при описании структуры волновых пучков в цилиндрической системе координат
{r,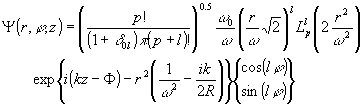 , (1.2.5)
, (1.2.5)
где
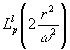 - обобщенный полином Лагерра, p и l - соответственно радиальный и угловой индексы, определяющие изменений знака поля в радиальном и азимутальном направлениях, d
0 l – символ Кронекера.
- обобщенный полином Лагерра, p и l - соответственно радиальный и угловой индексы, определяющие изменений знака поля в радиальном и азимутальном направлениях, d
0 l – символ Кронекера.
Как и для случая прямоугольных координат, разность фаз зависит от индексов моды и определяется уравнением
: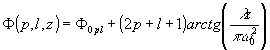 . (1.2.6)
. (1.2.6)
где F
0pl - начальная фаза.Как Эрмит-Гауссовы, так и Лагерр-Гауссовы моды, реализуемые на практике, характеризуются, как правило, большим значением радиуса кривизны волнового фронта. Поэтому их с хорошей степенью приближения можно отнести к поперечным электромагнитным волновым пучкам вида
TEM. С учетом поперечных индексов, в дальнейшем для этих пучков будут использоваться обозначения TEMmn и TEMpl соответственно.§1.3. Оптические сингулярные кристаллы и их свойства
В сингулярной оптике получил распространение термин
“оптический сингулярный кристалл”. Оптическим сингулярным кристаллом называется амплитудно-фазовая распределение суперпозиции вырожденных по частоте Эрмит-Гауссовых или Лагерр-Гауссовых мод, волновой фронт которой имеет резко выраженную сингулярную структуру с неизменной формой распределения винтовых дислокаций. Внешнее сходство между расположением ВД в поперечном сечении многомодового пучка с расположением ионов в кристалле и послужило основанием для введения вышеупомянутого термина. Дополнительное сходство обусловлено тем, что эквифазные линии в пучке имеют такую же структуру, как и силовые линии электрического поля в кристалле (см. например рис. 4). Оптический сингулярный кристалл может быть образован суперпозицией мод, развернутых по азимуту относительно друг друга на некоторый угол j и произвольно сдвинутых по фазе на величину q вдоль оси z. При этом поперечные индексы мод, входящих в суперпозицию должны удовлетворяют условию m+n=const (2p+l=const). Наиболее характерные для сингулярного кристалла формы распределения поля получаются при j и q равными ± p /2. В этом случае нулевые линии действительной и мнимой частей поля будут ортогональны и винтообразное вращение фазы вокруг точки дислокации равномерно. Для указанных условий распределение поля рассматриваемой суперпозиции мод можно записать в виде: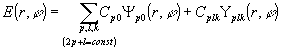 , ( k=1,2 ) (1.3.1)
, ( k=1,2 ) (1.3.1)
где
Cp0 и Cplk произвольные амплитудные весовые коэффициенты,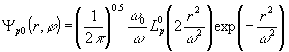 ,
,
(1.3.2)
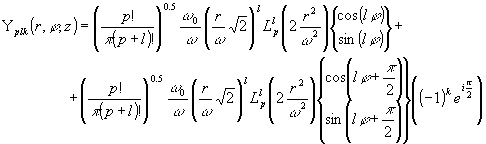 . (1.3.3)
. (1.3.3)
Выражение (1.3.2) характеризует распределение поля моды, в которой отсутствуют азимутальные нулевые линии (
l=0). Выражение (1.3.3) определяет суперпозицию Лагерр-Гауссовых мод, формирующих винтовую структуру волнового фронта в результате взаимного поворота на угол 900 и дополнительного смещения по фазе на p /2 . Моды Y p0 и U plk образуют полную систему ортогональных функций, по который может быть разложена любая суперпозиция мод, удовлетворяющих условию m+n=const (2p+l=const).Характерные экспериментальные распределения интенсивности светового поля вырожденных сингулярных кристаллов при 2p+l=2 и 2p+l=3
приведены на рисунке (1.3).
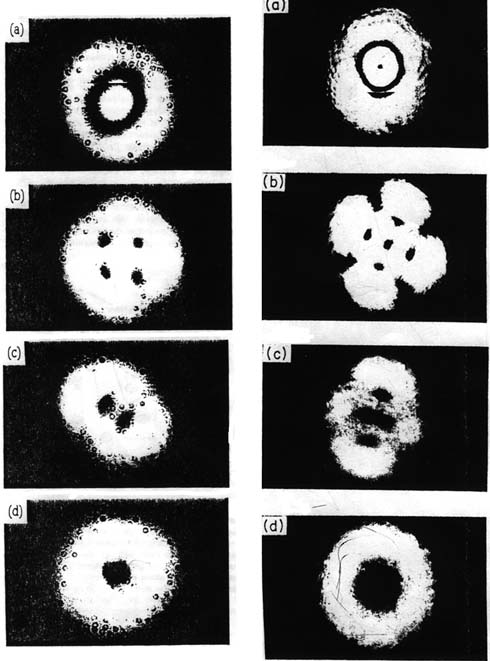
2p+l=2 2p+l=3
Рисунок 1.3.
Экспериментальные распределения интенсивности светового поля сингулярных кристаллов (2p+l=2 и 2p+l=3).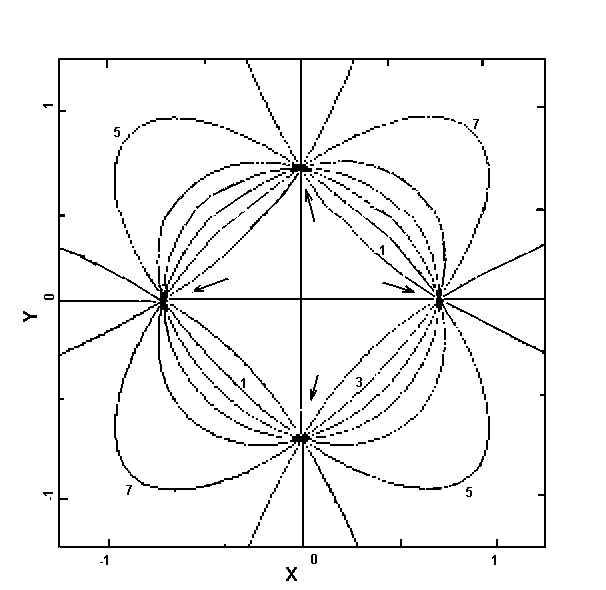
Рис. 1.4. Эквифазные линии поля оптического кристалла для суммы индексов
2p+l=2 (сравни рис. 1.3b). “1”=p /4, “3”=3p /4, “5”=5p /4, “7”=7p /4. Стрелками указано расположение винтовых дислокаций.§1.4. Методы идентификации винтовых дислокаций
Образование ВД на волновом фронте лазерных пучков является чисто фазовым эффектом. Поэтому, на основе анализа лишь распределения интенсивности в лазерном пучке, зарегистрировать распределение фазы в световых колебаниях в области ВД не представляется возможным. Единственным способом, обеспечивающим надёжную идентификацию ВД, является способ, основанный на использовании интерферометрической информации.
Самым удобным, с точки зрения обработки, является способ, основанный на регистрации структуры интерференции исследуемого поля с плоской или сферической однородными когерентными волнами.
На интерферограммах (по сути речь идет о голограммах волнового фронта) ВД даёт характерную особенность
: в точке дислокации интерференционные полосы ветвятся (рис. 1.5).
Рисунок 1.5.
Образцы представления ВД на интерферограмме.Слева дислокация 1-го порядка, справа - 2-го порядка
Разветвление интерференционной полосы (
“вилка”) является критерием дислокации на волновом фронте.Идентификация положения ВД по точкам ветвления интерференционных полос может осуществлена как в реальном, так и модельном экспериментах. В последнем случае анализу подвергается, структура интерферограммы, смоделированной на компьютере путем сложения полей синтезированного многомодового пучка и плоской (или сферической) однородной волны. При компьютерном моделировании и анализе структуры волны с фазовыми сингулярностями может быть использован еще один способ регистрации местоположения ВД. Он основан на выше описанном факте совпадения ВД с точками пересечения нулевых линий дествительной и мнимой частей комплексной амплитуды.
Часть II. Описание программной оболочки и интерфейса компьютерной задачи
Программа написана на языке
Borland Delphi 3.0 и представляет собой 32-битное приложение, работающее в Win 95, Win NT. Для работы с программой необходим компьютер IBM PC класса не ниже Pentium с 32 Mb ОЗУ.Программа позволяет строить как единичные моды (Лагерр-Гауссовы и Эрмит-Гауссовы), так и их сложные суперпозиции.
§ 2.1.
Рекуррентные формулы для расчетов полиномов Эрмита и ЛагерраВ программе для расчета полиномов Эрмита используются следующие рекуррентные соотношения:
![]() , (2.1a)
, (2.1a)
![]() , (2.1b)
, (2.1b)
![]() . (2.1c)
. (2.1c)
Для получения значения полинома
Hm(x) нужно вычислить в цикле (m-1) раз его значение, подставляя на следующем шаге значение предыдущего.Используемые в программе для расчета полиномов Лаггера рекуррентные соотношения имеют вид:
![]() , (2.2a)
, (2.2a)
![]() , (2.2b)
, (2.2b)
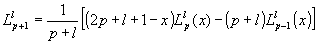 . (2.2c)
. (2.2c)
Для получения значения полинома
§ 2.2. Нормировки, используемые в программе
В программе моды свободного пространства нормированы на единичную мощность в плоскости, перпендикулярной оси
z.Вследствие дифракции световых пучков при увеличении значения продольной координаты
z, картина поля расплывается. Но наша цель - проследить за изменением местоположения нулевых линий комплексной амплитуды поля и соответственно, движением винтовых дислокаций. Поэтому целесообразно ввести нормировку для поперечных координат x и y в единицах w :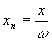 ,
, 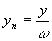 ,
, 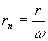 . (2.3)
. (2.3)
Далее, введем параметр
bF, который будет определять границу раздела между дальней и ближней зонами Френеля: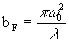 . (2.4)
. (2.4)
Удобнее рассматривать величины продольной координаты в долях параметра
bF: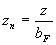 . (2.5)
. (2.5)
§ 2.3.
Дополнительные параметры, используемые в программеС целью получения более полного описания винтовых дислокаций поля с использованием суперпозиции мод, были введены следующие дополнительные параметры:1). Угол поворота осей y
- угол, задающий поворот осей OX и OY относительно начальной системы координат; 2) “Нормировочный” коэффициент А, характеризующий соотношение амплитуд, участвующих в суперпозиции мод;3) Смещение центра каждой из мод относительно начала координат x, y.
§ 2.4.
Описание интерфейса программыПрограмма имеет расширенный интерфейс и позволяет пользователю строить амплитудно-фазовые распределения любой сложности и проводить анализ структуры фазового поля двумя способами
: методом голограмм и методом нулевых линий. Главное меню и окно параметров программы приведено на рис. 2.1.Рисунок 2.1.
Главное меню и окно параметров системы моделирования суперпозиций сингулярных волновых пучков.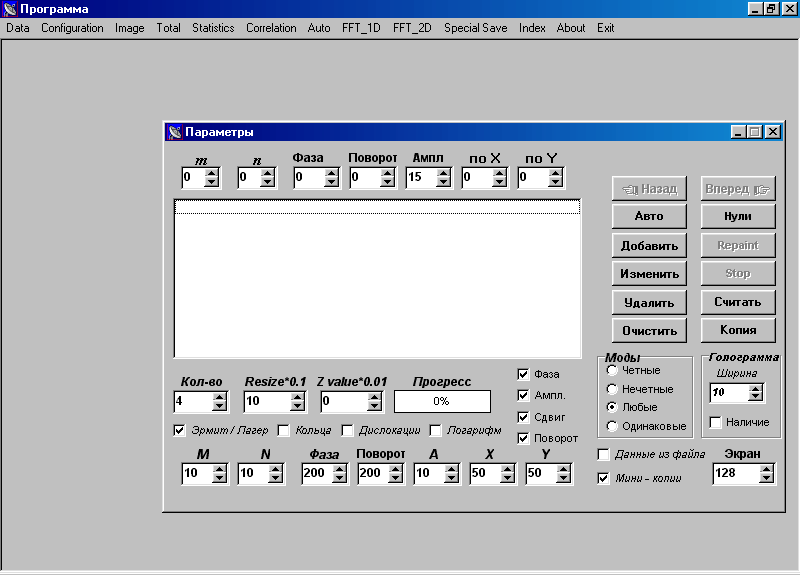
Выбор базиса разложения происходит путем инициализации соответствующего пункта
‘Эрмит/Лагерр’ соответственно. Пользователь может построить распределение интенсивности в изображении пучка в линейном и логарифмическом масштабе (переключатель ‘Логарифм’). Путем изменения размера матрицы (количества точек) пользователь имеет возможность получения как тестового изображения (маленькое окно), так и качественного изображения (большое окно); диапазон варьирования количества точек лежит от 128 до 512 точек ( параметр ‘Экран’ ). Варьирование размера рабочей зоны ( в единицах w ) производится путем изменения параметра ‘Resize’. В программе имеется возможность обновления уже считанной информации ( кнопка ‘Repaint’ ).В программе предусмотрено сохранение результатов в формате 256 цветов и 16 бит (опция
‘Image’ главного меню). При необходимости пользователь может считывать и сохранять результаты в формате данных: массивов действительной и мнимой частей комплексной амплитуды поля. Помимо этого в программе заложена возможность записывать и считывать конфигурации суперпозиций мод (пункт ‘Configuration’ главного меню).Ввод моды в суперпозицию осуществляется путем выбора значений следующих параметров
: ‘m’ (первый поперечный индекс), ‘n’ (второй поперечный индекс), ‘Фаза’ (начальная фаза), ‘Поворот’ (угол поворота), ‘Ампл.’ (вес данной моды в суперпозиции), ‘по X’ (сдвиг по X), ‘по Y’ (сдвиг по Y) в соответствующие верхние окна и последующим нажатием кнопки ‘Добавить’. Суперпозиция введенных мод высвечивается в нижнем окне. Для исключения (удаления) моды из суперпозиции, необходимо выделить моду из списка и затем нажать кнопку ‘Удалить’. Для полной очистки ранее набранного списка нужно нажать кнопку ‘Очистить’.Изменение текущего значения любой составляющей суперпозиции осуществляется следующим образом
: 1) выбрать нужную составляющую суперпозиции; 2) изменить текущие значения данной составляющей: ‘m’ (первый поперечный индекс), ‘n’ (второй поперечный индекс), ‘Фаза’ (начальная фаза), ‘Поворот’ (угол поворота), ‘Ампл.’ (вес данной моды в суперпозиции), ‘по X’ (сдвиг по X), ‘по Y’ (сдвиг по Y); 3) нажать кнопку ‘Изменить’. Параметр ‘Z value’ – продольная координата z, нормированная на величину параметра w .Программа имеет 4 режима автоматической генерации мод (
кнопка ‘Авто’ ) серии ‘Моды’: ‘Четные’, ‘Нечетные’, ‘Любые’, ‘Одинаковые’. Одинаковые моды – моды, имеющие одинаковые значения поперечных индексов. Программа позволяет генерировать случайные суперпозиции мод как четных (‘Четные’), нечетных (‘Нечетные’), произвольных (‘Любые’) мод. Количество генерируемых мод регулируется изменением параметра ‘Кол-во’. Предельные значения для суперпозиции генерируемых мод для автоматической генерации задаются в окнах верхних индексов мод (окна ‘M’ (первый поперечный индекс), ‘N’ (второй поперечный индекс), ‘Фаза’ (начальная фаза), ‘Поворот’ (угол поворота), ‘А’ (вес данной моды в суперпозиции), ‘X’ (сдвиг по X), ‘Y’ (сдвиг по Y).Для инициализации и прерывания процесса счета используются кнопки Считать и
Stop соответственно.В программе заложена возможность просмотра распределения светового поля
по определенному скану в плоскости поперечных координат (опция ‘Correlation / Срез’ главного меню). Подведя курсор мыши к точке изображения, мы получаем распределение интенсивности по x при фиксированном y и распределение интенсивности по y при фиксированном x.§ 2.5.
Анализ полученных структурОдной из важных функций программы является анализ полученных структур на предмет положения нулевых линий и наличия винтовых дислокаций.
Первый метод – метод нулевых линий (кнопка
‘Нули’).Этот метод регистрации позволяет с хорошей степенью точности определять местоположение винтовых дислокаций и часто используется для регистрации ВД в синтезированных структурах.
Второй способ анализа – метод голограмм (группа параметров
‘Голограмма’ ).Для того, чтобы получить соответствующую фазовую информацию, необходимо смоделировать интерферограмму внутри лазерного поля. Её моделирование сводится к расчету структуры поля, получаемого путем наложения на рассчитанную суперпозицию
TEM мод плоской однородной волны, направленной под небольшим углом z к оси распространения световой волны.При этом амплитуда интерферограммы будет определяться выражением:
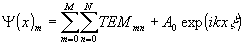 , (2.6)
, (2.6)
где
A0 - амплитуда плоской волны; x - угол наклона плоской волны к оси резонатора.
Выражение для интенсивности поля интерферограммы получим, если просуммируем квадраты действительной и мнимой частей последнего выражения:
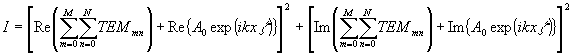 (2.7)
(2.7)
§ 2.6.
Примеры моделирования суперпозиций модПример 1.Моделирование единичной моды
TEM31Сначала необходимо выбрать тип мод (Эрмит-Гауссовы), далее в окне параметров устанавливаем значения
m=3 n=1 для поперечных индексов моды и нажатием кнопки ‘Добавить’ заносим набор значений в нижнее окно. Выбирая значение параметра Resize и продольной координаты z и дальнейшим расчетом (кнопка “Считать”) распределения интенсивности добиваемся оптимального заполнения рабочей области. После того,как получена изображение на экране (рис. 2.2 а), проводим анализ структуры поля методом нулевых линий поля (кнопка “Нули”) и получаем распределение рис. 2.2 б (опция Дислокации включена). Из рисунка видно, что действительная и мнимая части поля совпадают, в связи с чем на экране изображены только линейные дислокации.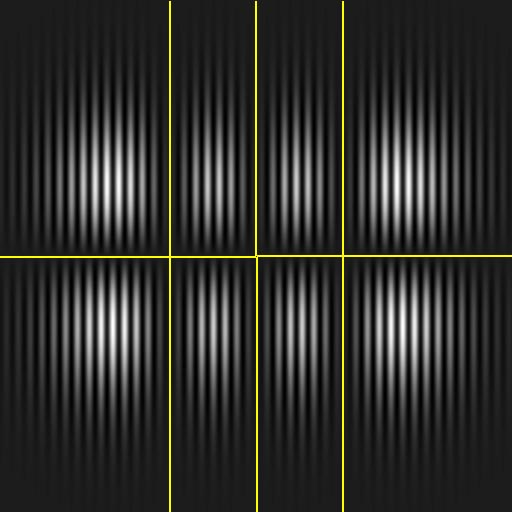

б
Рисунок 2.2. Мода
TEM31а - распределение интенсивности,
б - голограмма и структура нулевых линий
( Re-
зеленые,Im- синие линии, желтые линии-общие ).Пример 2. Моделирование суперпозиции вырожденных по частоте нечетных мод, поперечные индексы которых меняются от нуля до восьми при случайном разбросе начальных фаз и случайной ориентации осей симметрии
Сначала выбираем количество мод в суперпозиции (параметр
‘Кол-во’) и их тип (опция ‘Моды’). Далее, выбирая значение параметра Resize и величину продольной координаты z. Нажимаем кнопку “АВТО”, получая при этом в окне “Параметры” набор коэффициентов для построения суперпозиции мод. Далее нажимаем кнопку “Считать” и получаем на экране картину распределения интенсивности, добиваясь оптимального заполнения рабочей области. После того,как получена изображение на экране (рис. 2.3 а), проводим анализ структуры поля методом нулевых линий поля (кнопка “Нули”) и получаем распределение рис. 2.3 б. Далее, для анализа структуры поля методом голограмм необходимо в меню Голограмма выделить опцию Наличие, далее (опытным путем) установить значение параметра Ширина (ширина полос). Для построения голограммы не нужно производить перерасчет структуры, достаточно перестроить (кнопка Repaint) ранее расчитанную суперпозицию с новыми параметрами. В результате, получаем структуру, изображенную на рис. 2.4а и 2.4б (с нулевыми линиями).

б
Рисунок 2.3 Суперпозиция четырех поперечных мод
а - распределение интенсивности,б – структура нулевых линий (Re- зеленые,
Im- синие линии).
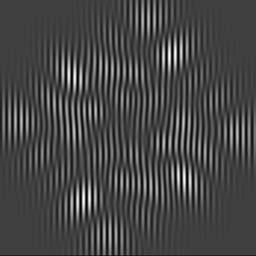
б
Рисунок 2.4 Суперпозиция четырех поперечных мод
а – голограмма, б – голограмма и структура нулевых линий (Re- зеленые,
Im- синие линии).
Часть III. Моделирование волновых пучков с винтовой структурой волнового фронта. Формулировка заданий
Задание 1.
Получить пучок с винтовой структурой волнового фронта путем сложения Эрмит-Гауссовых мод TEM10 и TEM01.Вызвать файл
Lab28.exe из указанной преподавателем директории. Используя метод нулевых линий, определить: при каком соотношении фаз и амплитуд мод результирующая мода будет характеризоваться равномерным азимутальным вращением фазы. Предъявить преподавателю изображение пучка (распределение интенсивности в поперечном сечении), а также его голограмму, полученную при помощи сферической опорной волны. Определить величину топологического заряда ВД.Задание 2.
Получить пучок с ВД второго порядка путем сложения Лагерр-Гауссовых мод.Предъявить преподавателю изображение пучка (распределение интенсивности в поперечном сечении), а также его голограмму, полученную при помощи сферической опорной волны.
Задание 3.
Смоделировать поле, представляющее случайную суперпозицию из 10 вырожденных по частоте нечетных мод, отличающихся поперечными индексами и значениями начальной фазы.Определить
: количество и расположение ВД в произвольной поперечной плоскости. Оценить соотношение между положительными и отрицательными ВД. Установить, какому виду симметрии удовлетворяет положение ВД. Выяснить, как меняется количество, расположение ВД и их симметрия при изменении расстояния от плоскости горловины. Построить график зависимости количества винтовых дислокаций как функцию продольной координаты zn. Предъявить преподавателю изображения пучка для ближней и дальней зон дифракции с нанесенными на них нулевыми линиями действительной и мнимой частей амплитуды. По оси z для трех произвольно выбранных ВД оценочно определить “длину свободного пробега” дислокаций (в нормированных единицах zn).Задание 4
. Синтезировать пучок, пространственная структура которого соответствует сингулярному кристаллу, определяемому суперпозицией Лагерр-Гауссовых мод при заданной преподавателем серии параметров.Определить: вид симметрии расположения ВД в поперечном сечении. Предъявить преподавателю изображения пучка для ближней и дальней зон дифракции с нанесенными на них нулевыми линиями действительной и мнимой частей амплитуды.
Рекомендуемая литература
Содержание
Часть
I. Общетеоретические сведения 2§ 1.1.
Природа фазовых сингулярностей,типы дислокаций волнового фронта
2§ 1.2. Амплитудно-фазовая структура лазерных
пучков. Моды свободного пространства 5
§ 1.3. Оптические сингулярные кристаллы и
их свойства 7
§ 1.4. Методы идентификации винтовых дислокаций 11
Часть II. Описание программной оболочки и
интерфейса компьютерной задачи
13§ 2.1.
Рекуррентные формулы для расчетовполиномов Эрмита и Лагерра
13§ 2.2.
Нормировки, используемые в программе 14§ 2.3.
Дополнительные параметры, используемыев программе
15§ 2.4.
Описание интерфейса программы 16§ 2.5.
Анализ полученных структур 19§ 2.6.
Примеры моделирования суперпозиций мод 20Пример 1.Моделирование единичной моды
TEM31 20Пример 2. Моделирование суперпозиции
вырожденных по частоте нечетных мод
22Часть III.
Моделирование волновых пучков с винтовойструктурой волнового фронта. Формулировка заданий 25
Литература
27