Задача практикума N 26
"Интерференционные явления в пучках с топологическими искажениями волнового фронта"
Оглавление
Упражнение 1. Обработка изображений 9
3.1.1. Ввод и первичная обработка изображений 10
3.1.2. Снятие характеристик изображений 11
Упражнение 2. Исследование структуры спекл-полей 11
ЛИТЕРАТУРА
ВВЕДЕНИЕ
Данная имитационная компьютерная задача знакомит студента с явлением интерференции света при различных типах интерферирующих волн. При этом особое внимание уделяется интерференции волн с аберрациями и топологическими возмущениями волнового фронта. Кроме того, на примере интерферометра поперечного сдвига изучается принцип работы интерферометров - приборов, осуществляющих такую интерференцию. При выполнении задачи вырабатывается “оптическая интуиция” - способность без вычислений чувствовать зависимость одних параметров интерференции от других и качественно оценивать действующие факторы. Студент учится настраивать интерферометр и применять его для оценки характеристик образцов.
Задача реализована в виде программы для ПЭВМ типа IBM PC (желательно 386 и выше). Запускаемый файл —linza.exe. Программа требует драйвера мыши от ‘Microsoft’ и русификатора с фонтами 8x8. Все действия студент производит самостоятельно за исключением .... Для работы с задачей необходимо знать основы функционирования IBM PC и устройства файловой системы MS-DOS [4].
Отчет по каждому упражнению состоит в сохранении определенных изображений или нахождении необходимых параметров. Сохраненное в виде файла изображение при сдаче задания предъявите преподавателю.
Правила безопасности: не редактировать файлы config.sys, autoexec.bat, не стирать никакие файлы.
ТЕОРЕТИЧЕСКАЯ ЧАСТЬ
Интерференция монохроматических плоских и сферических волн, а также волн с аберрациями волнового фронта подробно рассмотрена в многочисленных литературных источниках (см., например[1-4]). Существенно меньше в литературе имеется сведений относительно интерференции волн с дислокационной структурой волнового фронта, Поэтому в теоретической части ограничимся рассмотрением интерференции волн с фазовыми дислокациями.
От обычных аберраций волнового фронта дислокации отличаются тем, что принципиальным образом меняют топологию его поверхности. Дислокации возникают там, где линии смены знака действительной и мнимой частей комплексной амплитуды световых колебаний полностью или частично совпадают или пересекаются. В первом случае можно говорить, что вдоль общего для линий участка располагается линейная дислокация (ЛД); во втором - применительно к точке пересечения линий используются понятие винтовой дислокации (ВД). ЛД свойственен противофазный характер световых колебаний по обе её стороны. Основное же свойство ВД состоит в том, что при обходе вокруг неё фаза меняется на 2
p . В зависимости от направления “закрутки” волнового фронта все ВД подразделяются на левые и правые. Графическая иллюстрация поведения синфазной поверхности вблизи ВД дана на рис.1. Примером линейной дислокации могут служить узловые линии в поперечном сечении Эрмито-Гаусссовых (Лагерра-Гауссовых) мод ТЕМmn. Представление же о ВД дает приосевая область моды ТЕМ10· , являющейся суперпозицией сдвинутых по фазе на Pi/2 мод ТЕМ01 и ТЕМ10.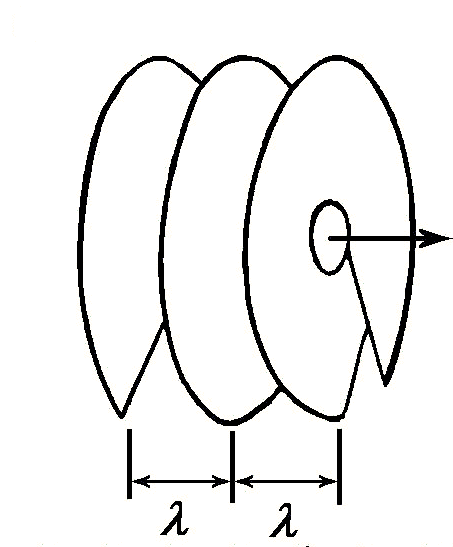
С точностью до постоянных фазовых множителей поле вблизи ВД может быть представлено в виде
u=Cxx+Cyy, (1)
где C
x, Cy - произвольные комплексные константы. Меняя ориентацию декартовых осей Х и У в плоскости сечения пучка, одну из них можно сделать действительной. Если Cx=± Cy =С, тоu=C
· r· exp(± ia ), (2)где
a - азимутальный угол. Последнее выражение описывает ВД с равномерным азимутальным вращением фазы. Если коэффициент Cx (Cy) равен нулю, то ВД переходит в ЛД, располагающуюся вдоль оси X(Y). Поскольку ЛД можно рассматривать как предельный случай неоднородной ВД, в дальнейшем основной акцент будет делаться на изучение свойств ВД.Теоретически можно представить, что в одной точке будут пересекаться несколько пар линий смены знака. Тогда в этой точке возникнет ВД более высокого порядка. Для нее будет характерно азимутальное изменение знака на величину 2
Pi l, где целое число l определяет порядок дислокации. В случае равномерного вращения фазы для поля ВД l-го порядка может быть использовано выражение:u=C
· r· exp(± ila ). (3)Заметим, что ВД порядка
l могут формироваться в устойчивых резонаторах на оси Лагерро-Гауссовых мод c азимутальным индексом, равным l. В общем виде поля этих мод характеризуются в поперечном сечении следующим радиальным распределением:upl=fpl(r/w)(apleil
a + bple-ila ), (4)где w параметр ширины распределения, f
pl(t) - обобщенный полином Лагерра, аpl, bpl - произвольные комплексные постоянные. Чаще встречающаяся в литературе формула для uplupl~fpl(r/w)cosla (5)
является частным случаем выражения (4), когда b
pl=apl. Именно формуле (5) и соответствуют, как правило, наблюдаемые в эксперименте модовые структуры.Яркое проявление находят ВД в световых полях с развитой спекл-структурой. Они были зарегистрированы в спекл-полях, образующихся при пропускании света через неоднородные фазовые пластины, а также многомодовые световоды
/ Выполненный применительно к спекл-полям анализ позволил обосновать ряд важных закономерностей. Среди них можно отметить выводы о равном числе правых и левых ВД, о неустойчивости ВД высокого порядка, о примерном равенстве числа дислокаций и числа спеклов.Наиболее прямой путь извлечения информации о степени
искажения волнового фронта лазерных пучков под влиянием дислокаций состоит в получении и обработке интерферометрической информации. Интерферограммы поперечного сечения пучка могут быть получены различным способами. Самый удобный с точки зрения обработки является способ основанный на регистрации структуры интерференции исследуемого поля с плоской или сферической однородными волнами. Однако практическое осуществление этого способа сталкивается о трудностями получения опорной волны. Такая проблема возникает, когда сам исследуемый лазер генерирует пучки со сложным распределением поля. Аналогичная ситуация имеет место, если исследуются искажения пучков прошедших большие расстояния. Обойти указанную трудность в ряде случаев удается за счет использования в качестве опорной волны расширенного участка волнового фронта с однородным распределением амплитуды и фазы. С тем, чтобы отличать интерферограммы, полученные с использованием однородной опорной волны, от других типов интерферограмм, мы будем в дальнейшем называть их голограммами.Другой подход к получению интерферомерических данных основан на применении двухкоординатных интерферометров поперечного сдвига. В последних осуществляется интерференция исследуемого пучка с пучком, сдвинутым в поперечном направлении. Получающиеся интерферограммы, хотя и имеют более сложную структуру, чем голограммы, несут полную информацию о волновом фронта и при соответствующей обработке позволяют выявить все его особенности.
Рассмотрим голографические “портреты” ВД при различной структуре и ориентации опорной волны. Будем для простоты считать, что опорная волн и
волна, несущая дислокацию, имеют единичную амплитуду. Если плоская опорная волна соосна с ВД, то поле голограммы при условии равномерного вращения фазы дислокаций будет определяться выражением:u
где параметр
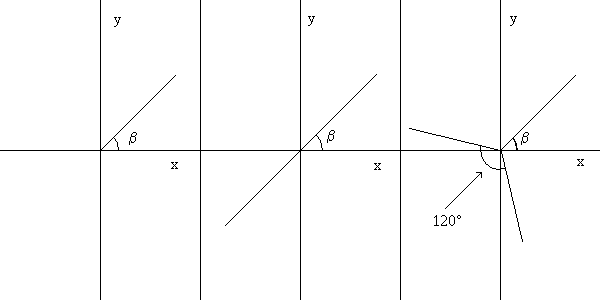
b характеризует фазу опорной волны. Используя (6), несложно убедиться, что положение на голограмме темных интерференционных полос будет таким, как показано на рис.2. Из рис.2 видно, что увеличение порядка дислокаций на единицу приводит к появлению на голограмме дополнительной радиальной темной полосы. Отметим, что входящий в (6) случайный параметр b не влияет на общую геометрию интерференционной картины.
Рис.2. Голограммы ВД первого, второго и третьего порядков (плоская опорная волна)
Если в качестве опорной волны взять соосную сферическую волну, то поле голограммы будет иметь вид
:![]() , (7)
, (7)
где R - радиус кривизны фронта сферической волны,
l - длина волны. Переходя к нормированной величине радиуса-вектора![]() . (8)
. (8)
На рис.3,а,б показана структура темных линий на интерферограмме для ВД первого и второго порядков. 3десь же пунктиром изображено первое темное кольцо интерференционной картины, получающейся в том случае, если со сферической волной вместо волны с дислокацией интерферирует плоская волна. Из рисунка видно, что ВД характеризуются спиральными интерференционными полосами. При этом степень
“закрученности” ВД зависит от ее порядка. Как и в предыдущем случае, параметр b не влияет на общую структуру интеферограммы. Его изменение приводит лишь к повороту спиралей вокруг оси. Если ось ВД смещена относительно оси опорной сферической волны, то структура ннтерферограмм претерпевает изменения. Их характер виден из рис.3,в,г. ВД первого порядка порождает на голограмме одну дополнительную полосу, ВД второго порядка - две полосы. Рассмотрим теперь важный в практическом отношении случай, когда на ВД падает под углом плоская волна. Поле, регистрируемое голограммой, для такого типа опорной волны примет вид:u
е =eila +eikx rcosa +ib (9)Рассчитанное на основе (9) расположение темных полос на голограмме для
b =0, l=1,2 приведено на рис.3,д,е. Здесь же для сравнения приведены полосы, которые получались бы, если бы вместо пучка с ВД была плоская волна. Сравнение показывает, что наличие ВД приводит к возмущению интерференционных полос, уменьшающемуся с удалением от дислокации. В местах присутствия ВД появляются дополнительные полосы, число которых равно порядку дислокации. Разветвление полос в точке ВД является общим для них свойством. Правые и левые дислокации будут иметь противоположные разветвления. Важным в методическом плане моментом является то, что распределение интенсивности поля в области разветвления будет зависеть от параметра b . На рис. 4 приведено распределение интенсивности вблизи ВД для разных b . Стрелкой указан участок, где имеется локальный минимум интенсивности. Наличие этих минимумов придает интерферограмме в области ВД устойчивый Y- образный вид.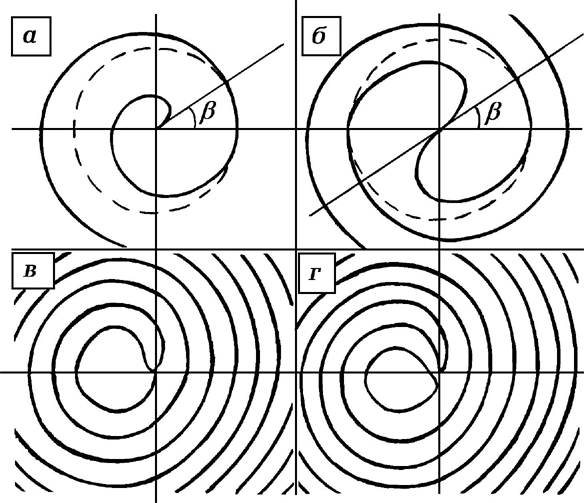
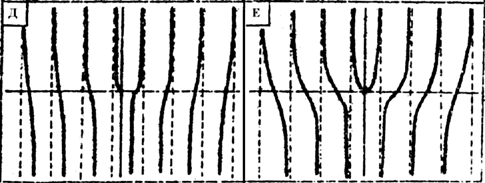
Рис.3. Структура темных линий голограмм волны с ВД.
а,б -сферическая опорная волна;
в,г -сферическая опорная волна со смещением;
слева - ВД 1-го порядка; справа - ВД 2-го порядка;
д,е - плоская опорная волна
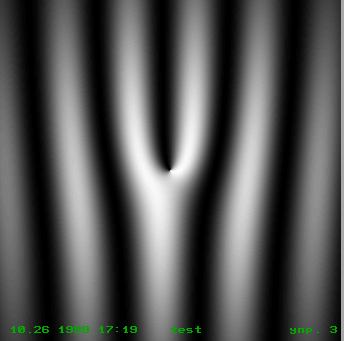
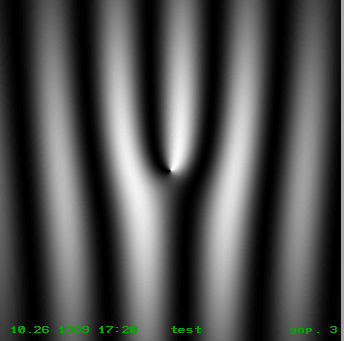
Рис.4. Распределение интенсивности на голограммах в области разветвления полос
Р
ассмотрим теперь особенности структуры интерферограммы поперечного сдвига. Регистрируемое интерферограммой поле u можно найти, складывая поле, определяемое формулой (1), с единичным полем, сдвинутым по координате x на величину x0 и наклоненным на угол x :u
е =u(x,y)+u(x+x0,y)eikxx -ib . (10)Здесь параметр
b будет характеризовать разность фаз между полями, возникающую при разделении пучков в интерферометре. Если сдвиг осуществляется по оси y и равен y0 тоu
е =u(x,y)+u(x,y+y0)eikxx -ib (11)Рассчитанное с помощью формул (10) и (11) положение темных полос на интерферограммах сдвига в присутствии ВД показано на рис.5.
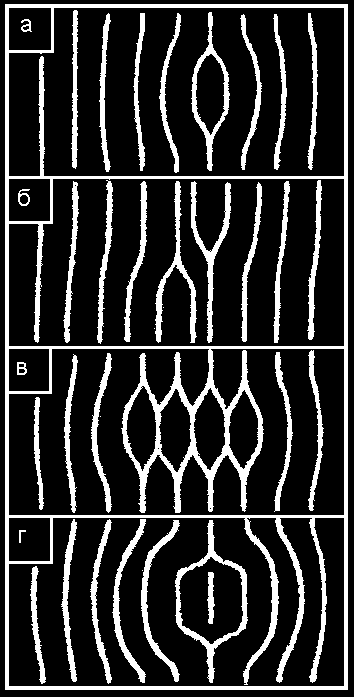
.
ПРАКТИЧЕСКАЯ ЧАСТЬ
НАЧАЛО РАБОТЫ
Сразу после запуска программы на экране появляется так называемое заглавное меню. Из него будут доступны все четыре упражнения. Перед началом работы введите в окошке "введите Ваше имя" свою фамилию. Каждое упражнение выбирается нажатием соответствующей кнопки в заглавном меню. (На всякий случай разъясняем. Здесь и далее под кнопкой понимается соответствующим образом выделенная экранная область, а под ее нажатием - щелчок в этой области при помощи “мыши”.)
УПРАЖНЕНИЕ №1
Интерференция плоских волн
В первом упражнении рассматривается элементарная интерференция плоских волн. Опорная волна интерферирует с предметной, параметры обоих задаются через углы падения к нормали экрана в двух перпендикулярных плоскостях, и разность фаз двух волн в центре пересечения пучков. Углы падения первой волны по двум взаимно перпендикулярным плоскостям обозначаются как alf1 и bet1, углы падения второй волны- alf2 и bet2.
Внизу расположена панель с интерференционной картиной, которая обновляется при каждом изменении параметров волн. Для ускорения работы размеры интерферограммы сделаны небольшими, а разрешение - невысоким. Если вы хотите посмотреть на более тщательно рассчитанную интерференционную картину, щелкните мышью на панели с интерферограммой — она прорисуется подробнее, правда, это займет несколько большее время.
Задания
1. Получите картину интерференции двух плоских волн.
2. Меняя различные параметры, посмотрите, как влияет каждый из них на вид интерференционной картины.
3. Сохраните одну из интерферограмм (какая вам больше понравится) при помощи команды
“результат\создать, save” верхнего меню. Отцените величину периода интерференционной картины для одного из указанных в приложении источка длины волны 0.63мкм.
УПРАЖНЕНИЕ №2
Интерферометр Маха-Цандера
Из заглавного меню (упражнения\меню) перейдите к упражнению №2. Появится панель моделирования интерферометра Маха-Цандера. Модель состоит из интерферометра Маха-Цандера когерентного источника света и экрана, на котором воспроизводится интерферограмма. Параметры зеркал и тип лазера можно изменять; для этого надо щелкнуть мышью на соответствующем элементе на схеме. Центры зеркал и пластинок двигаются в трех направлениях, а их наклон меняется в плоскости экрана и перпендикулярно ей. Источники света выбираются из ограниченного набора, приведенного в приложении (1).
Задания
1. Изменяя возможные параметры различных элементов, проследите, на что и как влияет каждый из них.
2. Меняя настройку, получите интерференционную картину в виде полос под углом 45 градусов (центры интерферирующих пучков должны совпадать). Сохраните в файл полученную картину.
3. Получите интерференционную картину в виде частично перекрывающихся пучков, центры которых лежат на диагонали экрана, а область интерференции составляет лишь часть пучков - область их пересечения. Приблизительный вид результата задания показан на рис.#. (Обращаем ваше внимание, что это самое трудное задание. Для его выполнения надо четко представлять, какие параметры интерферометра на что влияют и заранее предусмотреть, что и куда будете двигать. Выполнить это задание, меняя настройки наугад, невозможно.) Сохраните в файл полученную картину.
УПРАЖНЕНИЕ №3
Интерференция волн сложного фaзового профиля
Из заглавного меню перейдите к третьему упражнению. Вы увидите тот же экран, что и в первом упражнении. Вверху расположены диалоговые панели для выбора параметров первой и второй интерферирующих волн. Типы интерферирующих волн можно менять, выбирая из ограниченного набора (сферическая, плоская, цилиндрическая, винтовая дислокация, линейная дислокация, гауссов фазовый профиль, спекловая). На обеих панелях первоначально установлены параметры по умолчанию - "плоская". При выборе типа волны под данной диалоговым элементом разворачивается панель с индивидуальными параметрами волны выбранного типа. (описание свойств волн смотри в приложении (2) Все без исключения параметры волн можно изменять, правда, в ограниченном диапазоне.
Задания
1. Сочетая различные типы волн и меняя их параметры, получите несколько интерференционных картин. Ввиду большого числа параметров возможно, вам удастся получить нечто ранее невиданное. Можете записать понравившуюся интерферограмму.
2. Получите одну из интерферограмм, изображенных на рисунках 2 (а-е), которую укажет вам преподаватель. Какие использовать для этого типы волн и с какими параметрами, вы должны догадаться сами, опираясь на опыт, полученный в предыдущем задании. Сохраните полученные изображения.
УПРАЖНЕНИЕ №4
Интерферометр сдвига; обратная интерференционная задача
В этом упражнении с помощью интерферометра сдвига исследуются неровности на фазовой пластинке (Ф.П.). В качестве интерферометра сдвига используется такой же, как во втором упражнении - интерферометр Маха-Цандера. Ф.П. схематично отображается в одном плече интерферометра. Под Ф.П. находится диалоговое окно, с помощью которого можно вносить/извлекать Ф.П. в область прохождения предметной волны. Таким образом можно получить информативную (с объектом) и опорную (без объекта) интерферограммы.
Задания
1. Поместите фазовый объект в плечо интерферометра. Настройте интерферометр так, чтобы при удалении объекта интерференционная картина не исчезала. Запишите информативную и опорную интерферограммы.
2. Рассматривая и сравнивая полученные интерферограммы, оцените максимальную высоту неровностей на фазовом объекте (прозрачной пластинке). Показатель преломления пластинки принять равным 1.5, длину волны лазера возьмите из приложения.(1)
Литература
Приложение 1; Длины волн лазеров
Лазер 1 - 600нм, лазер 2 - 400нм, лазер 3 - 550нм, лазер 4 - 500нм, нелазерный источник - 400нм.