diplom

МОСКОВСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ имени М.В.Ломоносова ФИЗИЧЕСКИЙ ФАКУЛЬТЕТ КАФЕДРА ОПТИКИ И СПЕКТРОСКОПИИ _______________________________________ ДИПЛОМНАЯ РАБОТА (HTML сокращенная версия) А.М. Зотова ПО ТЕМЕ:

МЕТОДЫ АНАЛИЗА ФАЗОВЫХ ХАРАКТЕРИСТИК ЛАЗЕРНЫХ СИСТЕМ СО СЛОЖНОЙ СТРУКТУРОЙ ПОЛЯ ИЗЛУЧЕНИЯ

НАУЧНЫЕ РУКОВОДИТЕЛИ:

д.ф.-м.н. П.В. Короленко

к.ф.-м.н. Н.Н. Федотов

Зав. кафедрой
д.ф.-м.н., проф. Михайлин В.В. Москва 1999

оглавление

ВВЕДЕНИЕ
   ПОНЯТИЯ ПОЛЯ С ИСКАЖЕНИЯМИ ВОЛНОВОГО ФРОНТА ТИПА ВИНТОВЫХ ДИСЛОКАЦИЙ
   ЭКСПЕРИМЕНТАЛЬНЫЕ МЕТОДЫ ОБНАРУЖЕНИЯ ВИНТОВЫХ ДИСЛОКАЦИЙ
1 УЧЕБНАЯ ЗАДАЧА ПО ИНТЕРФЕРЕНЦИИ
   КРАТКОЕ ОПИСАНИЕ ЗАДАЧИ
   МОДЕЛИРУЕМЫЕ ТИПЫ ВОЛН
   АППАРАТНЫЕ ТРЕБОВАНИЯ ПРОГРАММЫ
2 ВРЕМЕННЫЕ ХАРАКТЕРИСТИКИ ЛАЗЕРНЫХ ПУЧКОВ; СНЯТИЕ "ПРОТЯЖЕК"
   МЕТОДЫ ПОЛУЧЕНИЯ ДИНАМИЧЕСКИХ ДАННЫХ
   СОЗДАННЫЙ МЕТОД МЕТОДЫ ПОЛУЧЕНИЯ ПРОТЯЖЕК
3 МЕТОДЫ ПРЕДСТАВЛЕНИЕ СЛОЖНЫХ АМПЛИТУДНО-ФАЗОВЫХ РАСПРЕДЕЛЕНИЙ ПОЛЯ
   МЕТОД НУЛЕВЫХ ЛИНИЙ КОМПЛЕКСНОЙ АМПЛИТУДЫ ПОЛЯ
   ГОЛОГРАФИЧЕСКИЙ МЕТОД ПРЕДСТАВЛЕНИЯ
   МЕТОД ФАЗОВОЙ ПАЛИТРЫ
   МЕТОД АМПЛИТУДНО-ФАЗОВОЙ ПАЛИТРЫ
4 МОДЕЛИРОВАНИЕ РАСПРОСТРАНЕНИЯ СЛОЖНЫХ ЛАЗЕРНЫХ ПУЧКОВ
   МЕТОД ТОЧЕЧНЫХ ИСТОЧНИКОВ
   ВЫЯВЛЕННЫЕ СЛУЧАИ РАСПРОСТРАНЕНИЯ
       РЕГУЛЯРНОЕ РАСПРОСТРАНЕНИЕ СВЕТОВЫХ ПУЧКОВ
       КВАЗИ-ПЕРИОДИЧЕСКОЕ ИЗМЕНЕНИЕ СТРУКТУРЫ ПУЧКА ПО МЕРЕ РАСПРОСТРАНЕНИЯ
     хаотические поля
   МАТЕМАТИЧЕСКАЯ ИНТЕРПРИТАЦИЯ НЕКОТОРЫХ ПОЛУЧЕННЫХ РЕЗУЛЬТАТОВ И ЕЕ СЛЕДСТВИЯ

ВВЕДЕНИЕ

ПОНЯТИЯ ПОЛЯ С ИСКАЖЕНИЯМИ ВОЛНОВОГО ФРОНТА ТИПА ВИНТОВЫХ ДИСЛОКАЦИЙ

Значительная часть современной оптики посвящена анализу различного рода аберраций и причин их возникновения. Существуют и подробно описаны оптические аберрации всевозможных типов.[] При этом основное внимание уделяют аберрациям, которые состоят в отступлении формы волнового фронта от плоской или сферической без изменения топологии. В их число входят простейшие искажения волнового фронта, при которых каждая эквифазная поверхность остается однолистной функцией, а волновой фронт обычно представляет собой семейство поверхностей, отстоящих друг от друга приблизительно на расстояние одной длины волны. Однако существуют оптические аберрации и принципиально иного класса, связанные с образованием топологических особенностей на поверхности волнового фронта, заметным образом влияющие на свойства излучения. Они возникают как непосредственно в оптических устройствах, так и при распространении света в передающих средах. Изучение аберраций, сопровождающихся изменением топологии, представляет на сегодняшний день большой интерес, т.к. они являются менее изученной частью оптики. Главным элементом в описании изменения топологии является понятие винтовой дислокации. При этом любые самые сложные искажения волнового фронта можно описывать с помощью комбинации возмущений без изменения топологии и винтовых дислокаций. Достаточно строгое и развёрнутое описание особенностей оптического поля в окрестности винтовых дислокаций дано в работе [1]. Изложим кратко суть природы винтовых дислокаций. Винтовыми дислокациями волнового фронта (ВД) будем называть точки фронта волны, при обходе вокруг которых в плоскости, перпендикулярной к направлению распространения, фаза изменяется на величину +/-2*Pi. Под "фазой" здесь понимается аргумент комплексной амплитуды поля. В зависимости от того, какой знак имеет набег фазы вокруг ВД, различают правые и левые дислокации. Существует другой подход к описанию ВД. Дислокацию можно представить как точку пересечения линий смены знака действительной и мнимой частей амплитуды поля. Винтовые дислокации являются атрибутами волнового фронта лазерных пучков со спекловой структурой. Такие пучки могут формироваться либо в резонаторах лазеров при наличии заметных неоднородностей [12], либо в случайно-неоднородных средах (в том числе турбулентной атмосфере) [5]. Хотя статистические характеристики спекловых полей рассматривались во многих работах, некоторые закономерности, связывающие, в частности, уровень пространственных и временных флуктуаций фазы, изучены еще недостаточно. Проведение исследований в указанном направлении затруднены несовершенством способов представлений и идентификации топологических искажений.

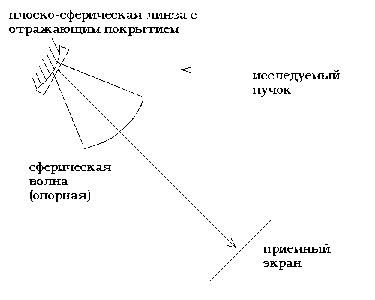
ЭКСПЕРИМЕНТАЛЬНЫЕ МЕТОДЫ ОБНАРУЖЕНИЯ ВИНТОВЫХ ДИСЛОКАЦИЙ

Для извлечения фазовой информации при проведении реальных измерений часто используют различного типа голографические приставки и интерферометры, располагающиеся в приемном тракте оптической системы. [17] В качестве наиболее простой и в то же время весьма надежной голографической приставки часто используют интерферометр радиального сдвига, схема которого изображена на рисунке 1.1. Его основным элементом является плоскосферическая линза, на сферическую поверхность которой, нанесено отражающее покрытие. В результате наложения световых пучков, отраженных соответственно от плоской и сферической поверхностей линзы, формируется интерференционная картина радиального сдвига, анализ которой, позволяет выявить наиболее характерные типы фазовых возмущений. В данном интерферометре роль опорной волны выполняет сферическая волна, на ВФ которой, на достаточном расстоянии от линзы, появляются участки с относительно равномерным распределением фазы, целиком перекрывающие площадь волны с плоским фронтом. Эти области образованы, за счет масштабирования сферической волны. Для наибольшего контраста интерференционной картины параметры линзы, коэффициент отражения и расстояние до экрана подбираются в соответствии с условием равной интенсивности опорной и предметной волн.

Рис. 1.1.(а) Схема интерферометра радиального сдвига.

Рис. 1.1.(б) Пример голограммы, позволяющей идентифицировать одиночное ВД, при использовании интерферометра радиального сдвига.

Часто при проведении интерференционных измерений для регистрации фазовых характеристик используют методы сдвиговой интерферометрии. Обычно при этом используют интерферометры типа Маха-Цандера. Принцип действия интерферометра иллюстрирует рисунок 1.2. Этот интерферометр позволяет определять такие характеристики лазерных пучков, как кривизну и локальные наклоны волнового фронта, топологические особенности профиля фазы. Используемый интерферометр представляет систему плоских полупрозрачных и глухих зеркал, которая осуществляет наложение исследуемого поля на идентичное, сдвинутое в поперечном направлении на величину h и наклоненное относительно исследуемого на угол a. Преимущество данного интерферометра состоит в том, что величины h и a в процессе его настройки могут изменяться независимым образом.

Рис. 1.2.(а) Схема регистрации винтовых дислокаций, возникающих в лазерном резонаторе на базе интерферометра Маха-Цандера; 2,3-зеркала, 1,4-полупрозрачные пластинки, 5-приемный экран.

Рис. 1.2.(б) Пример интерферограммы сдвига, позволяющей идентифицировать одиночное ВД, при использовании интерферометра Маха-Цандера.

УЧЕБНАЯ ЗАДАЧА ПО ИНТЕРФЕРЕНЦИИ

ОПИСАНИЕ ЗАДАЧИ (Краткое описание задачи практикума N26 “Интерференционные явления в пучках с топологическими искажениями волнового фронта”)

     Данная задача знакомит студента с явлением интерференции при различных типах интерферирующих волн. Кроме того, изучается принцип работы интерферометров - приборов, осуществляющих такую итнтерференцию. При выполнении задачи вырабатывается “оптическая интуиция” - способность без вычислений чувствовать зависимость одних параметров интерференции от других и качественно оценивать действующие факторы. Студент учится настраивать интерферометр и применять его для оценки характеристик образцов.
     Отчет по каждому упражнению состоит в сохранении определенных изображений или нахождении необходимых параметров. Сохраненное в виде файла изображение при сдаче задания предъявите преподавателю.
     Ниже приведен список входящих в задачу упражнений:

1. Интерференция плоских волн

В первом упражнении рассматривается элементарная интерференция плоских волн. Опорная волна интерферирует с предметной, параметры обоих задаются через углы падения к нормали экрана в двух перпендикулярных плоскостях, и разность фаз двух волн в центре пересечения пучков.

2. Интерферометр Маха-Цандера

Изучаемая модель состоит из интерферометра Маха-Цандера, когерентного источника света и экрана, на котором воспроизводится интерферограмма. Параметры зеркал и тип лазера можно изменять; для этого надо щелкнуть мышью на соответствующем элементе на схеме. Центры зеркал и пластинок двигаются в трех направлениях, а их наклон меняется в плоскости экрана и перпендикулярно ей. Источники света выбираются из ограниченного набора, приведенного в приложении.

3. Интерференция волн сложного фaзового профиля

Вверху рабочего экрана расположены диалоговые панели для выбора параметров первой и второй интерферирующих волн. Типы интерферирующих волн можно менять, выбирая из ограниченного набора (сферическая, плоская, цилиндрическая, винтовая дислокация, линейная дислокация, гауссов фазовый профиль, спекловая). На обеих панелях первоначально установлены параметры по умолчанию - "плоская". При выборе типа волны под данной диалоговым элементом разворачивается панель с индивидуальными параметрами волны выбранного типа. (описание свойств волн смотри в приложении (2) Все без исключения параметры волн можно изменять, правда, в ограниченном диапазоне.

4. Интерферометр сдвига;
обратная интерференционная задача

В этом упражнении с помощью интерферометра сдвига исследуются неровности на фазовой пластинке (ФП). В качестве интерферометра сдвига используется такой же, как во втором упражнении - интерферометр Маха-Цандера. ФП схематично отображается в одном плече интерферометра. Под ФП находится диалоговое окно, с помощью которого можно вносить/извлекать ФП в область прохождения предметной волны. Таким образом можно получить информативную (с объектом) и опорную (без объекта) интерферограммы.

МОДЕЛИРУЕМЫЕ ТИПЫ ВОЛН

Все смоделированные в учебной программе волны определялись непосредственным заданием волнового фронта и амплитуды. Профиль амплитуды почти для всех типов волн выбран гауссовым. Для двулучевой интерференции возможно независимое задание пар волн следующих типов: с плоским ВФ, с сферическим ВФ, с циллиндрическим ВФ, профиль с ВД, профиль с ЛД, спекловое поле.
Сама задача с описанием находится здесь.

АППАРАТНЫЕ ТРЕБОВАНИЯ ПРОГРАММЫ

Задача реализована в виде программы для ПЭВМ типа IBM PC (от 386 и выше) и работает под MS-DOS. Запускаемый файл —linza.exe. Программа требует драйвера мыши от ‘Microsoft’ и русификатора с фонтами 8x8. Результаты упражнений сохраняются в формате grayscale bmp в директории с именем, совпадающим с именем студента.

ВРЕМЕННЫЕ ХАРАКТЕРИСТИКИ ЛАЗЕРНЫХ ПУЧКОВ; СНЯТИЕ "ПРОТЯЖЕК"

МЕТОДЫ ПОЛУЧЕНИЯ ДИНАМИЧЕСКИХ ДАННЫХ

Помимо информации о пространственных изменениях в распределении фазы световых колебаний, важное значение имеют данные о временных зависимостях фазовых характеристик. В рамках методов сдвиговой интерферометрии применялся фотомеханический способ регистрации [] происходящих во времени изменений структуры интерферограмм. Он был основан на пропускании сформировавшейся на выходе интерферометра сдвиговой интерферограммы через узкую щель, за которой располагалась движущаяся фотопленка. В тех случаях, когда щель сориентирована перпендикулярно направлению полос, регистрируемая на фотопленке "временная протяжка" интерферограммы, позволяла из анализа частоты и амплитуды изгиба полос оценивать спектр и характерные частоты фазовых флуктуаций. Точность определения высокочастотных составляющих спектра определяется скоростью движения фотопленки и ее чувствительностью.

СОЗДАННЫЙ МЕТОД МЕТОДЫ ПОЛУЧЕНИЯ ПРОТЯЖЕК

В разработанной измерительной системе была предусмотрена другая возможность получения временных протяжек, основанная на чисто электронных и программных средствах. Эта возможность состоит в регистрации системы сечений в последовательности полукадров интерференционной картины, регистрируемой при помощи специальной компьютерной платы видеозахвата, сопряженной с ПЗС-матрицей. ПЗС-матрица генерирует сигнал в телевизионном черно-белом стандарте SEKAM [16]. Формат этого аналогового сигнала следующий: изображение разбито на 625 строк, каждую 1/25 секунды передаются кадры, разделенные специальными импульсами, каждый кадр состоит из двух также разделенных синхроимпульсами полукадров, первый - с последовательностью четных строк, второй - с последовательностью нечетных. Во время разделительных импульсов, происходит обратный ход луча. Строки также отделены друг от друга разделительными импульсами, что необходимо для синхронизации процесса записи. Попадая на плату видеозахвата, аналоговые строки разбиваются на столбцы и оцифровываются 6-битным АЦП.

Рис. 2.1. Временное сечение интерферограммы, снятой с модели турбулентной cреды.

Рис. 2.2. Временное сечение автора диплома.

Из описания формата сигнала видно, что существует возможность отдельного захвата полукадров или соседних строк из разных полукадров с частотой 50 кадров в секунду. Чтобы реализовать эту возможность, были использованы специальные написанные на языке ассемблера функции. Наиболее важными из них являются следующие: Freeze — захват текущего изображения с данными параметрами и помещение изображения в буфер платы видеозахвата, и ReadDeviceBuffer — перенос захваченной информации в ОЗУ компьютера по соответствующему сегменту и смещению.

МЕТОДЫ ПРЕДСТАВЛЕНИЕ СЛОЖНЫХ АМПЛИТУДНО-ФАЗОВЫХ РАСПРЕДЕЛЕНИЙ ПОЛЯ

Как уже указывалось, распределение фазы в поперечном сечении лазерных пучков с ВД волнового фронта является весьма сложным. Обычные методы его представления, основанные на анализе структуры волновой поверхности, оказываются неэффективными. Существует проблема представления особенностей топологических искажений и идентификации положение ВД. В данном параграфе описаны некоторые способы и соответствующее программное обеспечение для реализации такой формы представления данных о фазе, которая позволяет в наглядной форме и с высокой степенью надежности выявлять положение и параметры ВД. Созданная программа работает как с собственным форматом файла APM (amplitude-phase map), в котором сохраняется амплитуда и фаза для каждой точки изображения, амплитуда при этом варьируется от 0 до 255, а фаза от 0 до 239, так и с парами ASCII файлов, в которых по отдельности сохраняется действительная и мнимая части. Ниже приведена серия рисунков иллюстрирующая возможности представления сложного поля разными методами.

Рис 3.1. Голографический метод представления.

Голографический метод представления заимствован из экспериментальной оптики. Согласно этому методу положение ВД может быть определено по областям ветвления интерференционных полос. Нами была разработана компьютерная версия этого метода, которая нашла реализацию при анализе результатов численного моделирования световых полей с дислокационной структурой ВФ.

Рис. 3.2. Метод нулевых линий.

Метод нулевых амплитуд был предложен в работе [1]. Согласно этому методу положение ВД может быть определено по точкам пересечения действительной и мнимой частей комплексной амплитуды светового поля. (красные и синии линии соответственно).

Рис 3.3. Метод фазовой палитры.

Описанный выше метод нулевых линий, а также его компьютерная реализация удобны прежде всего с точки зрения идентификации положения ВД. Однако они не позволяют оценивать значение фазы как в окрестности ВД, так и по всему сечению светового пучка. В работе [4] было предложено представлять распределение фазы с помощью специальной циклической палитры, каждому цвету в ней соответствует определенное значение фазы. Таким образом, точки, в ближайшей окрестности которых встречаются все цвета, соответствуют точкам ВД, а линии, вдоль которых цвет не меняется —эквифазным линиям.

Рис 3.4. Метод амплитудно-фазовой палитры.

Предложенная в [4] схема реализации метода, обладая рядом достоинств, тем не менее может быть усовершенствована. Она разрабатывалась несколько лет назад, когда высокоцветный режим использовался весьма редко. В настоящее время в режиме 16-битного представления цвета появилась возможность внедрить новую специальную цветовую палитру, отражающую амплитуду и фазу одновременно. Существующие методы представления изображений [14] не удовлетворяют необходимым требованиям.
Кратко задача разработка палитры сводится к следующему: нужно выбрать замкнутый контур (отображение фазы) в RGB пространстве так, чтобы при сдвиге этого контура к началу координат (отображение амплитуды) цветность и яркость указывали соответственно на значение фазы и амплитуды.

МОДЕЛИРОВАНИЕ РАСПРОСТРАНЕНИЯ СЛОЖНЫХ ЛАЗЕРНЫХ ПУЧКОВ

МЕТОД ТОЧЕЧНЫХ ИСТОЧНИКОВ

В данном параграфе рассматриваются вопросы динамики топологических искажений ВФ, которые предполагают исследования траекторий движения ВД и трансформации их структуры по мере распространения световых пучков в свободном пространстве. При этом мы ограничимся рядом наиболее распространенных случаев.
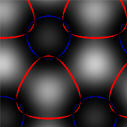
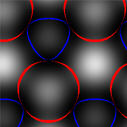
При моделировании структуры световых пучков будем считать, что их световое поле образовано в результате интерференции сферических волн, исходящих от точечных источников, находящихся в одной плоскости. Все случаи рассмотрены для центральной зоны пучка, находящейся в пределах порядка или более дифракционного угла. Поле в каждой точке рассчитывается как сумма комплексных полей от точечных источников. На рисунке 4.1. показано распределение интенсивности светового поля на плоском экране, находящемся в дальней зоне по отношению к системе случайным образом расположенных точечных источников. Здесь же приведены нулевые линии действительной и мнимой частей амплитуды поля (красные и синии линии соответственно). Расположение этих линий на периферии близко к системе близко расположенных окружностей. Это обстоятельство, являющееся следствием сферичности ВФ суммарной волны, затрудняет анализ распределения фазы и идентификацию ВД. В связи с этим целесообразно из итоговой фазы вычитать часть, связанную со сферичностью фронта волны. На рисунке 4.2. представлено то же поле, что и на рисунке 4.1. после указанной процедуры. Видно, что при вычитании фазового набега, обусловленного сферичностью ВФ, анализ распределения поля заметным образом упрощается.

Рис. 4.1. Распределение интенсивности и расположение нулевых линий действительной и мнимой частей амплитуды без учета сферичности ВФ.

Рис. 4.2. Распределение интенсивности и расположение нулевых линий действительной и мнимой частей амплитуды с учетом сферичности ВФ.

ВЫЯВЛЕННЫЕ СЛУЧАИ РАСПРОСТРАНЕНИЯ

"РЕГУЛЯРНОЕ" РАСПРОСТРАНЕНИЕ СВЕТОВЫХ ПУЧКОВ В ходе моделирования полей при различных расположениях точечных источников было установлено, что возможна реализация трех основных случаев формирования полей с дислокационной структурой ВФ. К первому случаю отнесем формирование в пространстве периодических световых полей близких по своей структуре к “сингулярным кристаллам” [15]. В зависимости от расположения и интенсивности точечных источников эти поля могут иметь весьма сложную структуру, однако основным их свойством является то, что форма распределения амплитуды и фазы в поперечном сечении суммарной волны остается неизменной. Было установлено, что такие поля могут формироваться в том случае, если точечные источники располагаются на одной окружности. При этом не существенным оказываются значение их интенсивности, фазы и направления радиус-векторов, определяющих их положение (смотри приложение 2). Этот эффект наблюдается в телесном угле, угол раскрыва которого имеет величину порядка (предполагается, что биссектриса угла, являющаяся оптической осью системы, перпендикулярна плоскости окружности и проходит через ее центр). На рисунке 4.3. в качестве примера приведено распределение поля для случая, когда на окружности располагается пять точечных источников, положение и фазы которых характеризуется величинами: (2Pi/5*N). Положение дислокаций, с точностью до масштабного множителя остается неизменными при распространении суммарной волны. Если ось системы сместить относительно центра окружности расположения точечных источников, то будет иметь место равномерное смещение структуры поля (включая ВД) в поперечном сечении по мере удаления от точечных источников. Анализ структуры сложных световых полей, моделируемых вышеуказанным образом, удобно осуществлять строя продольное распределение их интенсивности. На рисунках 4.3. приведены такие распределения для полей сохраняющих форму амплитудно-фазового распределения (а), а также для изменяющихся по мере распространения полей (б) в пределах 1000*a от плоскости источников. Из приведенных рисунков видно, что в случае поля сформированного источниками находящимися на окружности (а) продольное распределение интенсивности характеризуется бесконечными неизменными по форме фрагментами структуры. В случае же хаотического поля (б) структура поля характеризуется многочисленными спеклами имеющими случайное положение и различную продольную длину. Причем их длина увеличивается по мере удаления от плоскости источников в зависимости от величины 1/R. В общем случае структура спеклов по мере распространения меняется только в зависимости от радиальной координаты источников. (смотри приложение 2)

Рис. 4.3.(а) Продольное сечение пучка; пять источников расположенны на одной окружности.

Рис. 4.3.(б) Продольное сечение пучка; расположение четырех источников тоже, что и для Рис. 4.3. пятый источник находится на расстоянии 0.9 от радиуса общей окружности.

Рис. 4.3.(в) Продольное сечение пучка; расположение четырех источников тоже, что и для Рис. 4.3. пятый источник находится на расстоянии 0.5 от радиуса общей окружности.

КВАЗИ-ПЕРИОДИЧЕСКОЕ ИЗМЕНЕНИЕ СТРУКТУРЫ ПУЧКА ПО МЕРЕ РАСПРОСТРАНЕНИЯ Комбинирование разлиных положений источников выявило еще одну возможность распространения светового пучка, когда его структура периодически воспроизводится при распространении. При этом пространственный период повторений увеличивается пропорционально величине 1/Z и стремится к бесконечности в дальней зоне. Примечательным здесь является тот факт, что пучок являющийся бездислокационном в одном поперечном сечении, в дальней зоне, например, может иметь множество винтовых дислокаций. В связи с этим затруднена диагностика таких пучков. Из сопоставления приведенных рисунков видно, что в процессе распространения суммарной волны происходит попарное возникновение и исчезновение ВД с противоположным зарядом. На серии рисунков 4.4. продемонстрирован эффект периодического изменения структуры пучка от бездислокационного к структуре с ВД. На приведенном рисунке представлен один период.

Рис. 4.4. Периодическое изменеие структуры пучка по мере распространения.

ХАОТИЧЕСКОЕ ПОЛЕ Был рассмотрен случай случайного расположения источников в начальной плоскости, моделирующий хаотическое световое поле. В рассматриваемом случае наблюдался как процесс взаимодействия типа рождения и аннигиляции пар разноименных ВД, так и движение ВД через зону наблюдения. Аннигиляция ВД происходила вследствие “расцепления” линий действительной и мнимой частей амплитуды, а рождение — в результате появления их дополнительных пересечений. Первый из этих процессов иллюстрирует рисунок 2.5.6. на нем белым прямоугольником, размещенным в центре приводимых распределений показана область в которой происходит исчезновение (аннигиляция) двух разноименных ВД. На тех же рисунках белым прямоугольником, расположенном у верхней рамки рисунков, показана область, где первоначально локализованная ВД покидает рабочее поле. В общем случае траектории движения ВД и расстояния вдоль распространения световой волны на которых они существуют могут быть самыми разнообразными. Анализ трансформации дислокационной структуры случайного поля при плавном изменении z~ при z~>0.1 показал что длина “свободного пробега” ВД может меняться в очень широком диапазоне (от сотых и десятых долей до величины порядка 1). К общей закономерности преобразования ВФ случайного поля можно отнести тот факт, что количество дислокаций в выбранном угле распространения световой волны близко к некоторой постоянной величине при этом количество положительных ВД равно количеству отрицательных. Последнее свойство обусловлено вышеописанным сценарием попарного рождения и аннигиляции ВД.
Синтез амплитудно-фазовых распределений проводился с помощью специально созданной программы работающей с моделью точечных источников.